最小二乘法与matlab拟合工具箱cftool

一）关于最小二乘法

百度百科解释：

最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。

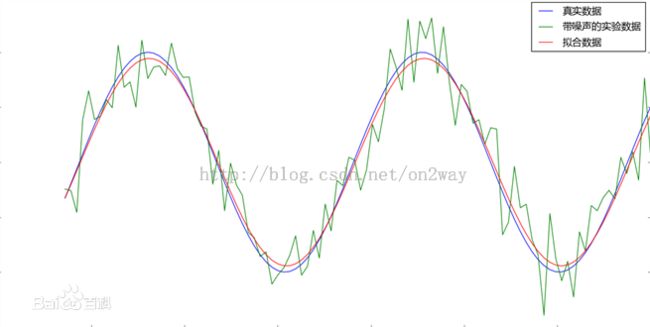
用于数据拟合，直观的认识如下图所示：实际中你的数据可能是绿线所表示的那样（当然多数时候是离散的点），很明显，这样的数据没有规律也不光滑，那么你想用一个光滑的多项式函数来表示这些数据怎么办？就得拟合，像红线所示的那样，拟合出来一条光滑的曲线，而且这个曲线的表达式还是可以知道的。知道了表达式的形式的另一个好处是求任意给定的x值求y值（比如你的数据是x=1,2,3...对应的y值，如果你想求x=1.5对应的y值怎么办？），或者是可以用于函数的预测（比如你的数据是x=1,2,3...10这10个数据对应的y值，你想求x=11对应的y值怎么办？）。

关于函数的拟合说明到这，那么具体如何根据得到的数据得到拟合函数的具体形式呢？这里就需要一种算法来实现了，这就是最小二乘法。当然在这之前，你也需要明白一下内容：

（1）你所拟合的函数形式是什么样子的？

比如上面的数据，你能得到一系列x值以及对应的y值，想要拟合，你是不是也需要知道y与x对应的函数关系？比如是sin（x）的关系，或者cos（x）的关系，亦或者是两者组合关系呢？这里我们随便假设一个：

y = a1*sin(x)+a2*cos(x)+a3*sin(x)*cos(x)

在这里可以看到，似乎又多出来了几个系数（a1,a2,a3）有木有？对了，这里我们所说的函数关系其实是x与y之间符合sin、cos和sin*cos的关系，但是他们之间具体是几倍关系，谁知道呢。从这里你也可以明晓的一点就是，最小二乘算法的函数拟合不是说跟你寻找到底是属于哪种关系，而是在你规定的关系上拟合出这些关系对应的系数（也就是寻找最优的a1,a2,a3），从这里你还可以明晓一点的就是，一旦你规定的关系不好，比如上面的，可以看出大概符合sin或者cos关系，你非要规定他们符合y = a1*x+a2*x^2,这样的关系，那么你也可以拟合出这样关系下的a1与a2,但是你会发现你的结果会非常差，很容易理解。

（2）判断是否最优的标准是什么？

有了上面的函数关系，下面就是寻找到这种关系下的系数了对不对？那么怎么评判一组系数（a1,a2,a3）比另一组系数（a1,a2,a3）要好呢，这就是最小二乘。

对于一组给定的系数后，你就相当于得到了一个函数关系，那么对于任意的x值，就会有一个实际值y和一个拟合值y’吧，那么对于所有的x值，最小二乘的就是求解下面公式的最小值：

公式很简单，简单描述就是求实际值与拟合值的误差（残差）平方和，也很容易知道，对于每一组系数（a1,a2,a3），势必会出现一个Y，算法的演变形式就是求取最小化Y对应的系数（a1,a2,a3）（有点像优化算法，当然完全可以用优化算法去求解）。

Ok到这，你应该知道了什么是最小二乘以及它的实用性问题了，下一步是如何求解这组系数了。

二）最小二乘求解

（1）老问题：关于函数关系：

这里再说一遍这个问题，有人可能会说，在实际问题中，我只能得到一系列的离散点，至于他们符合哪种函数关系谁知道呢？也是，要想知道完美的符合关系确实不可能，我们只能猜想到他们的近似函数关系，碰到这类问题，首先我们需要画出得到的离散点，看看他们大致符合哪种关系，然后去试吧（也没有好的方法—_—），当然后面会说到matlab自带的拟合工具箱，里面有很多函数关系，这就大大减少了你盲目去试的时间了。

一般来说，可能的函数关系（或者叫基函数）有：多项式、三角函数、指数函数、样条函数等。

（1）关于求解原理

这里我们假设已经知道了符合的函数关系了，比如像上面的那个函数关系：

y = a1*sin(x)+a2*cos(x)+a3*sin(x)*cos(x)

我们把这个函数划分开来，分为基函数和系数，那么基函数为：

对应的系数就为：

现在问题就转化为求待定系数：（a1,a2,a3）。即：

把这个式子再变一下：

那么由多元函数极值必要条件有：

对任意函数h(x)和g(x)，引入记法：

由于向量组线性无关，也就是上式的系数行列式，那么可以得到该函数的最小二乘解为：

解上述的这个正规方程组就可以得到最小二乘对于的系数：（a1,a2，...,an）;还是以上述那个式子为例可以看到，这里：

？？？表示视具体形式而定了；同时等式右边可以表示为：

其中的f就是实际对于变量x的y值。上述矩阵都是已知的，那么参数是可以直接算出来的。在进一步简化，把式子3.3.2写成为：

就可以求出参数W的值。这里X就可以表示每个基函数在所有自变量x下的值一个矩阵，方便理解，还是以上例说明：比如得到的数据是x=[1:10];得到的y是对应与x的平方，也就是y=[1,4,9,...,100]这10个数，现在我们想用

y = a1*sin(x)+a2*cos(x)+a3*sin(x)*cos(x)

这组函数来拟合数据（显然关系不对是吧），那么这里：

而Y直接就是[1,4,9,...,100]’;这样w就出来了。

三）关于matlab拟合工具箱cftool

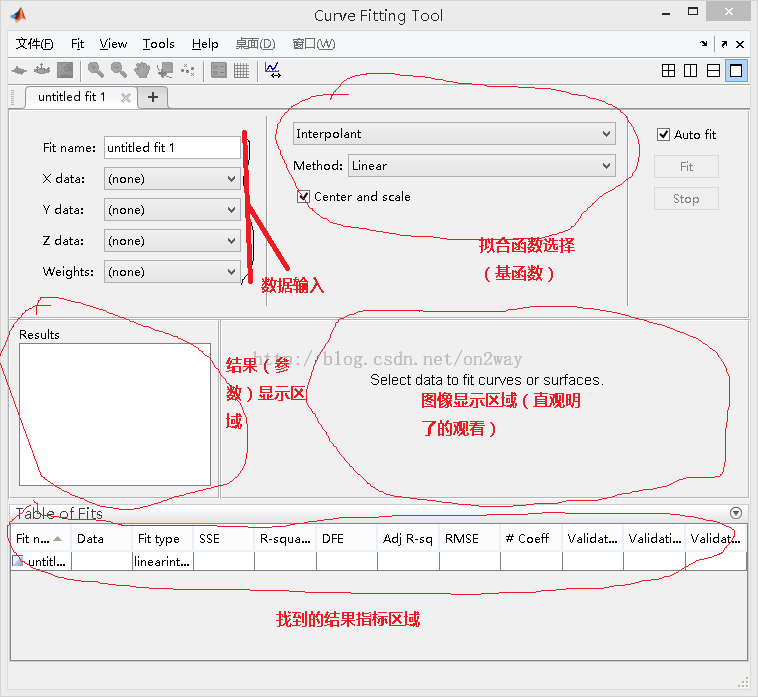
在matlab命令下，直接输入cftool即可以打开工具箱的界面：

现在给定一组需要拟合的数据如下（这是一幅图像的灰度统计图），具体怎么来的就不说了，想试验的可以自己假设数据，也很简单，这组数据中，假定x为1:247，对应当然也有247个y的值。

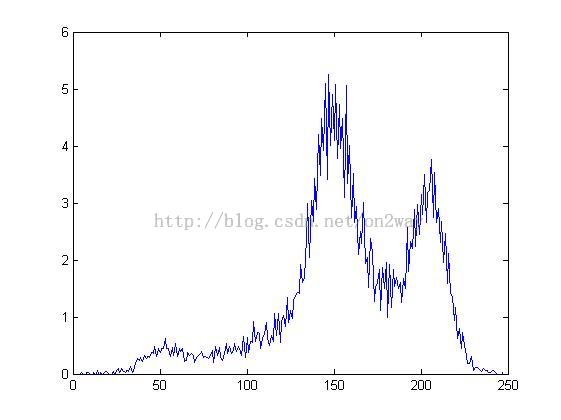
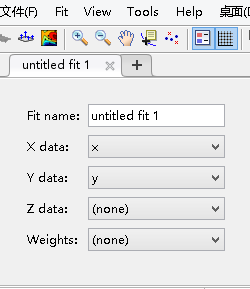
在matlab工作区一旦正确输入了x和y值以后，打开工具箱对应的数据输入处就会出现选项了，如下：

输入后选择方法：

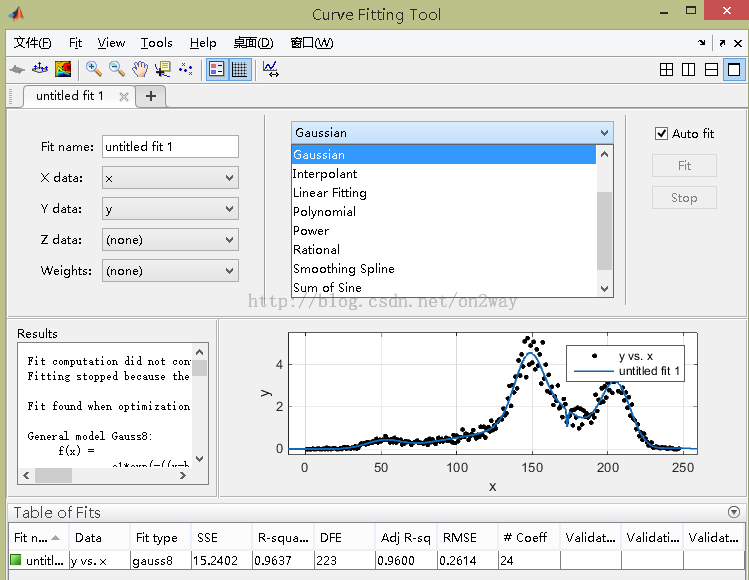
这里把参数设置成这样的：

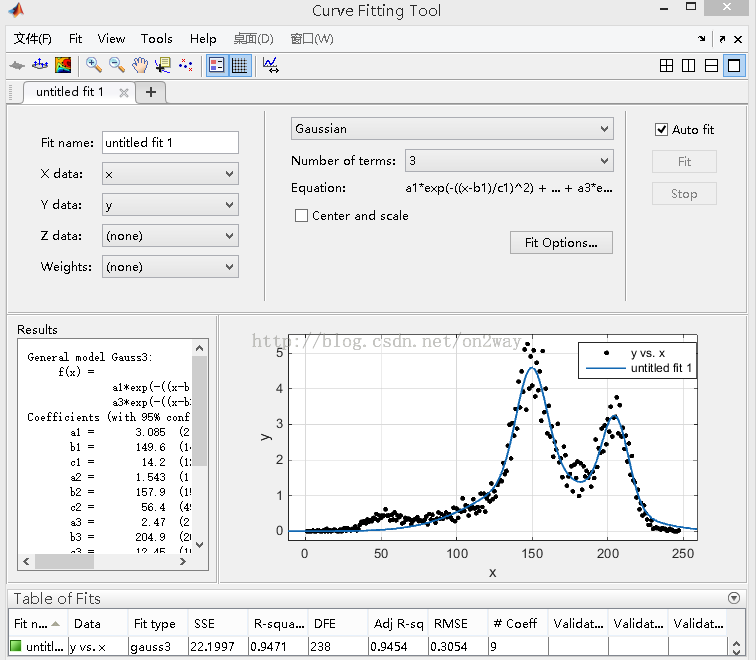
可以看到结果还是可以的，那么这是使用的高斯函数作为基函数，而且不是一个，是3个，具体的形式也可一看到如下：

这组基函数有9参数，值也分别可以看到，那么可以说我们这组数据的拟合形式就知道了。当然还有很多其他的显示可以自己一一尝试，一旦你改变基函数后，matlab会自动进行拟合，也不需要你去点什么。那么到底拟合结果怎么样呢？看最后一项评价值，比如看R-square,看SSe等等，具体表示什么可以百度。

四）关于程序实现

有的时候，我们不光要得到图，还要得到函数形式（用于预测，计算未知的x对应到y值等等），那么就有两种方式获得，一种方式：直接由上述工具箱得到函数形式以及函数参数，好了，在matlab里面自己把这个拟合函数编辑出来。

另一种方式：根据上述原理按公式计算得到，这里我们也可以对比一下按照原理计算出来的参数与工具箱计算出来的参数差多少（注意：工具箱得到的参数可能并不是按照最小二乘原理来的）。

还是以上述数据，这里我们的选择函数变一下：

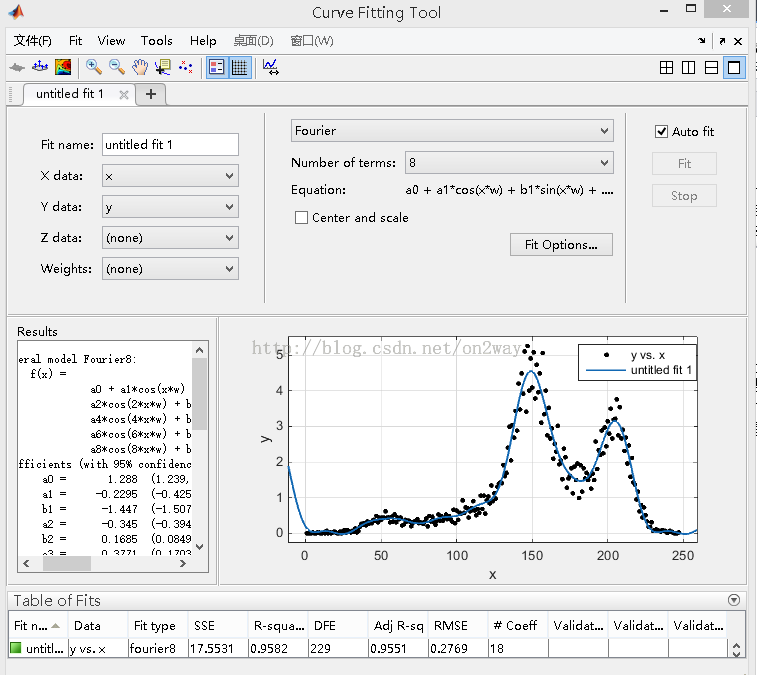
选择Fourier基函数，同时数目选择8（看看你和函数形式，很复杂对不），得到的参数也可以看到。

这个时候我们需要从这幅图中得到所有基函数形式，像这里就是[1,cos(w*x),sin(w*x),cos(2*w*x),...,sin(8*w*x)];有点不好办的是w在基函数里面，最小二乘法决定了在编程时不能把它作为需要求的参数，这里我们安札工具箱求出来的值w=0.02711来计算，这样根据原理就可以编写如下程序：

w = 0.02771;
X = [];
for i = 1:length(xx)
    x = xx(i);
    temp = [1;cos(w*x);sin(w*x);cos(w*2*x);sin(w*2*x);...
        cos(w*3*x);sin(w*3*x);cos(w*4*x);sin(w*4*x);...
        cos(w*5*x);sin(w*5*x);cos(w*6*x);sin(w*6*x);...
        cos(w*7*x);sin(w*7*x);cos(w*8*x);sin(w*8*x)];
    X = [X,temp];
end
Y = y’;
W = (X*X')^-1*X*Y;
figure;
plot(xx, Y', 'o', xx, W'*X);

自变量设置为xx了;这样结果如下：

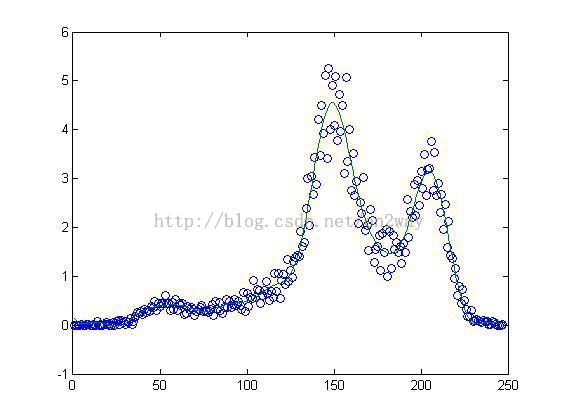
>> W'

ans =

  Columns 1 through 8

    1.2877   -0.2301   -1.4471   -0.3450    0.1687    0.3765   -0.4796   -0.4493

  Columns 9 through 16

   -0.5169   -0.2684    0.2232   -0.0070   -0.0012   -0.1665    0.0300    0.0000

  Column 17

0.1106

工具箱得到结果如下：

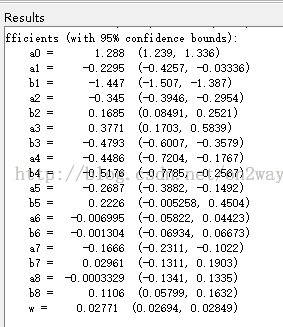
对比发现差的并不是很多。这就是最小二乘下的函数拟合。