C++程序设计实验报告(四十七)---第六周任务五
/* (程序头部注释开始)
* 程序的版权和版本声明部分
* Copyright (c) 2012, 烟台大学计算机学院学生
* All rights reserved.
* 文件名称:计算两点之间距离、到原点距离、关于坐标轴和原点的对称点(多文件)
* 作 者: 刘镇
* 完成日期: 2012 年 3 月 25 日
* 版 本 号: 1.043
* 对任务及求解方法的描述部分
* 输入描述: 两个坐标点。
* 问题描述: 设计平面坐标点类,计算两点之间距离、到原点距离、关于坐标轴和原点的对称点等
* 程序输出: 两点之间距离、到原点距离、关于坐标轴和原点的对称点
* 程序头部的注释结束
*/
头文件:
#include<iostream>
#include<cmath>
using namespace std;
class CPoint
{
private:
float x; // 横坐标
float y; // 纵坐标
public:
float Distance(CPoint p) const; // 两点之间的距离(一点是当前点,另一点为参数p)
void input(); //以x,y 形式输入坐标点
};
class CTriangle
{
public:
CTriangle(CPoint &X, CPoint &Y, CPoint &Z):A(X), B(Y), C(Z){} //给出三点的构造函数
void setTriangle(CPoint &X, CPoint &Y, CPoint &Z); //
float perimeter(void); //计算三角形的周长
float area(void); //计算并返回三角形的面积
bool isRightTriangle(); //是否为直角三角形
bool isIsoscelesTriangle(); //是否为等腰三角形
private:
CPoint A,B,C; //三顶点
};
主函数:
#include<iostream>
#include"Triangle.h"
using namespace std;
void main()
{
CPoint cp1, cp2, cp3;
cp1.input();
cp2.input();
cp3.input();
CTriangle c(cp1, cp1, cp1);
c.setTriangle(cp1, cp2, cp3);
cout << "三角形的周长是:" << c.perimeter() << endl;
cout << "三角形的面积是" << c.area() << endl;
cout << (c.isRightTriangle()?"是":"不是") << "直角三角形" <<endl;
cout << (c.isIsoscelesTriangle()?"是":"不是") << "等腰三角形" <<endl;
system("pause");
}
资源函数:
#include<iostream>
#include"Triangle.h"
using namespace std;
float CPoint::Distance(CPoint p) const
{
return sqrt((p.x - x) * (p.x - x) + (p.y - y) * (p.y - y));
}
void CPoint::input()
{
char c;
cout << "请输入点坐标:(格式:x,y)" << endl;
do
{
cin >> x >> c >> y;
if(c == ',')
{
break;
}
cout << "格式不正确,请重新输入:" << endl;
}while(1);
}
void CTriangle::setTriangle(CPoint &X, CPoint &Y, CPoint &Z)
{
float s1 = X.Distance(Y);
float s2 = Y.Distance(Z);
float s3 = X.Distance(Z);
if(s1 + s2 > s3 && s2 + s3 > s1 && s1 + s3 > s2)
{
A = X;
B = Y;
C = Z;
}
else
{
cout << "不能构成三角形,退出!" << endl;
exit(1);
}
}
float CTriangle::perimeter(void)
{
return (A.Distance(B) + B.Distance(C) + A.Distance(C));
}
float CTriangle::area(void)
{
float a = A.Distance(B);
float b = B.Distance(C);
float c = A.Distance(C);
float p = (a + b + c) / 2;
return sqrt( p * (p - a) * (p - b) * (p - c) );
}
bool CTriangle::isRightTriangle()
{
float a = A.Distance(B);
float b = B.Distance(C);
float c = A.Distance(C);
if(a * a + b * b == c * c || a * a + c * c == b * b || c * c + b * b == a * a)
{
return true;
}
else
{
return false;
}
}
bool CTriangle::isIsoscelesTriangle()
{
float a = A.Distance(B);
float b = B.Distance(C);
float c = A.Distance(C);
if(a == b || b == c || a == c)
{
return true;
}
else
{
return false;
}
}
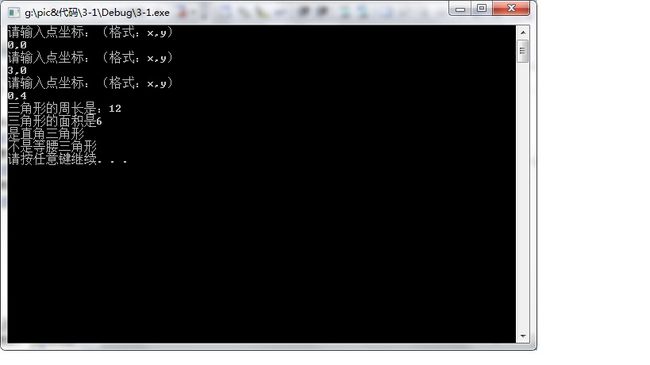
运行结果:
感言:
说感言,就是觉得如果类越多,体会出分多文件的好处,你将不同文件分离,处理错误的能力会有提高,效率也提高,因为是分割包围了嘛!重点突出,好解决。