【COCOS2DX-游戏开发之三六】圆与未旋转矩形的碰撞检测(上篇)

我们以cocos2dx lua脚本来说明，原理才是重点，本文参照了两种方法

第一种方法 

bool intersects(CircleType circle, RectType rect)
{   
    //1
    circleDistance.x = abs(circle.x - rect.x);
    circleDistance.y = abs(circle.y - rect.y);

   //2
    if (circleDistance.x > (rect.width/2 + circle.r)) { return false; }
    if (circleDistance.y > (rect.height/2 + circle.r)) { return false; }

   //3
    if (circleDistance.x <= (rect.width/2)) { return true; } 
    if (circleDistance.y <= (rect.height/2)) { return true; }

   //4
    cornerDistance_sq = (circleDistance.x - rect.width/2)^2 +
                         (circleDistance.y - rect.height/2)^2;

    return (cornerDistance_sq <= (circle.r^2));
}

circle.x, circle.y圆心 rect.x, rect.y 矩形的中心

Here's how it works:

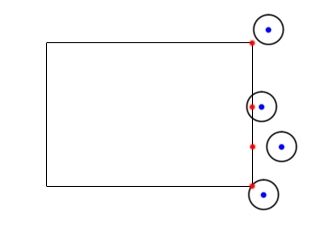
1.The first pair of lines calculate the absolute values of the x and y difference between the center of the circle and the center of the rectangle. This collapses the four quadrants down into one, so that the calculations do not have to be done four times. The image shows the area in which the center of the circle must now lie. Note that only the single quadrant is shown. The rectangle is the grey area, and the red border outlines the critical area which is exactly one radius away from the edges of the rectangle. The center of the circle has to be within this red border for the intersection to occur.


2.The second pair of lines eliminate the easy cases where the circle is far enough away from the rectangle (in either direction) that no intersection is possible. This corresponds to the green area in the image.


3.The third pair of lines handle the easy cases where the circle is close enough to the rectangle (in either direction) that an intersection is guaranteed. This corresponds to the orange and grey sections in the image. Note that this step must be done after step 2 for the logic to make sense.


4.The remaining lines calculate the difficult case where the circle may intersect the corner of the rectangle. To solve, compute the distance from the center of the circle and the corner, and then verify that the distance is not more than the radius of the circle. This calculation returns false for all circles whose center is within the red shaded area and returns true for all circles whose center is within the white shaded area.

原文链接：http://stackoverflow.com/questions/401847/circle-rectangle-collision-detection-intersection

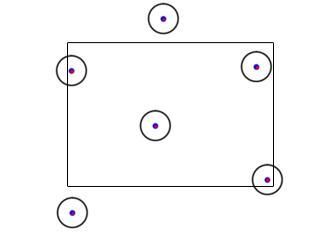
第二种方法 检测圆和矩形碰撞，要找到矩形上离圆的中心点最近的点 计算

if circle.x < box.x then
   cx = box.x
end

如果圆在矩形的左边，离着圆中心点最近的矩形上的点在矩形的左边边界上

elseif circle.x > box.x + box.width then
   cx = box.x + box.width

如果圆的中心点在矩形的右边，离着圆中心点最近的矩形上的点在矩形的右边边界上

else
   cx = circle.x

如果圆心x既不在矩形的左边也不在右边, 那么cx就在矩形内

同理，找到Y方向上离着圆中心点最近的y偏移cy

    if circle_pt.y < rect.y then
        cy = rect.y
    elseif circle_pt.y > rect.y + rect.height then
        cy = rect.y + rect.height
    else
        cy = circle_pt.y
    end

最后附上lua版的圆与矩形的碰撞，圆与圆的碰撞检测

--[[--

检测圆和未旋转的矩形之间的碰撞
参考:http://lazyfoo.net/SDL_tutorials/lesson19/index.php

~~~ lua

local intersects = circleIntersectRect(cc.p(10, 10), 50, cc.rect(20, 20, 100, 100))

~~~

param: circle_pt 圆心
param: radius 半径
param: rect 矩形 {x=0,y=0,width=100,height=100}

@see 

]]
function circleIntersectRect(circle_pt, radius, rect)
    local cx = nil
    local cy = nil

    -- Find the point on the collision box closest to the center of the circle
    if circle_pt.x < rect.x then
        cx = rect.x
    elseif circle_pt.x > rect.x + rect.width then
        cx = rect.x + rect.width
    else
        cx = circle_pt.x
    end

    if circle_pt.y < rect.y then
        cy = rect.y
    elseif circle_pt.y > rect.y + rect.height then
        cy = rect.y + rect.height
    else
        cy = circle_pt.y
    end

    if cc.pGetDistance(circle_pt, cc.p(cx, cy)) < radius then
        return true
    end

    return false
end


--[[--

检测圆之间的碰撞

~~~ lua

local intersects = circleIntersects(cc.p(10, 10), 10, cc.p(20,20), 20)

~~~

@param: circle_pt_a 圆A中心
@param: radius_a 圆A半径
@param: circle_pt_b 圆B中心
@param: radius_b 圆B半径

@return 是否碰撞

@see 

]]
function circleIntersects(circle_pt_a, radius_a, circle_pt_b, radius_b)
    -- If the distance between the centers of the circles is less than the sum of their radius
    if cc.pGetDistance(circle_pt_a, circle_pt_b) < (radius_a + radius_b) then
        return true
    end
    return false
end

参考:http://lazyfoo.net/SDL_tutorials/lesson19/index.php

下一篇 【COCOS2DX-游戏开发之三七】圆与旋转矩形的碰撞检测(下篇)