《算法导论》第十章——基本数据结构（一）：栈与队列

引言：算法操作的集合可以随着时间的改变而增大，减小，或者产生其他变化，我们称这种集合是动态的。接下来的五章，我们将研究计算机上表示和操作有穷动态集合的一些基本技术。本文主要为你讲解栈与队列的操作和实现，建议将这些操作制作成库，方便以后的引用，避免重复编码。系列文章为算法导论的笔记和相关习题解答。

本文来源：栈与队列

动态集合的元素

元素包括两个部分：关键字+卫星数据

动态集合上的操作

主要包括两个大的方面：查询

我们约定：集合为S，关键字为k，指向元素的指针为x

Search（S，k）

Inserrt（S，x）

Delete（S，x）

Minimum(S)

Maximum( S )

Successor (S,x)

Predecessor(S,x)

栈和队列

一、栈

实现了一种先进先出的策略。通常情况下我们采用数组加栈顶指示top来实现，约定top==0（或者-1）的时候表示栈为空；同时如果stack的长度是m，那么要考虑元素个数超过m以后产生的溢出问题。栈的一些定义和基本操作如下：

#ifndef MAXSTACKSIZE
#define MAXSTACKSIZE 200
#endif
typedef int StackDataType;
typedef struct mystack{
  int top;
  StackDataType data[MAXSTACKSIZE];
}Stack,*StackPointer;
extern int IsEmpty(Stack s); 
extern int Push(StackPointer s, StackDataType element);
extern StackDataType Pop(StackPointer s); 

注明：stack的数据结构还可以定义一个指针和大小，来取代数组。这些操作的实现方式如下：

#include"stack.h"
#include<stdlib.h>
#include<stdio.h>
StackDataType Pop(StackPointer s){ 
  if(s->top==-1){
    printf("the stack is already empty!\n");
    exit(1);
  }

  --(s->top);
  return s->data[s->top+1];
}

int IsEmpty(Stack s){ 
  if(s.top==-1){
    return 1;
  }
  else{
    return 0;
  }
}

int Push(StackPointer s,StackDataType element){
  if(s->top >= MAXSTACKSIZE-1){
    printf("the stack is over flow!\n");
    return 0;
  }
  ++(s->top);
  s->data[s->top]=element;
  return 1;
}

二、队列

我们可以把队列想象成排队等待服务的人群，同样也可以用 数组+对头指针+对尾指针 来实现队列这个数据结构；其中，head表示下一个要出列的元素，tail表示刚刚进入队列的元素。另外，为了实现环绕，我们需要把队列实现成为循环数组的模式，这个可以通过取模运算来实现。这样，head==tail+1表示队列已经满了；但是，此时我们会发现，如果我们让元素逐个出列，那么当最后一个元素出列的时候，同样满足head=tail+1；也就是说，队列在空和满的情况下具有相同的抽象条件。为了对此进行区分，我们用tail表示下一个进入队列的元素将要进入队列的位置,那么，初始化情况下，所以head=tail表示队列为空，初始情况下，head=tail=0；如果我们用head=tail+1表示队列为满的情况，意味着这个情况下，队列中有一个位置处于没有利用的状态，如果要利用这个元素，又会出现head=tail表示空和满两种情况。

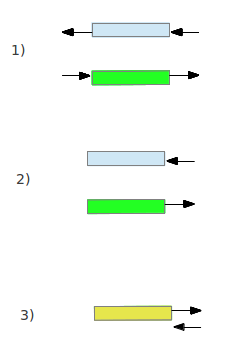
关于队列的一些操作实例可以看下图，从而理解上面一段中的相关情况：

队列的一些定义的基本的操作如下：

#ifndef MAXQUEUESIZE
#define MAXQUEUESIZE 200
#endif
typedef int QueueDataType;
typedef struct myqueue{
  int tail;
  int head;
  QueueDataType data[MAXQUEUESIZE];
}Queue,*QueuePointer;
extern int IsEmpty(Queue queue);
extern int IsFull(Queue queue);
extern int EnQueue(QueuePointer queuep, QueueDataType element);
extern QueueDataType DeQueue(QueuePointer queuep);

操作实现：

#include"queue.h"
#include<stdlib.h>
#include<stdio.h>
/*make sure the queue is not empty when you delete element from it*/
QueueDataType DeQueue(QueuePointer queue){
  if(queue->head==queue->tail){
    printf("the queue is already empty!\n");
    exit(1);
  }
  QueueDataType temp;
  temp=queue->data[queue->head];
  ++(queue->head);
  if(queue->head==MAXQUEUESIZE)//
    queue->head=0;
  return temp;
}

int IsEmpty(Queue queue){
  if(queue.head==queue.tail){
    return 1;
  }
  else{
    return 0;
  }
}
int IsFull(Queue queue){
  if(queue.head==(queue.tail+1)%MAXQUEUESIZE){
    return 1;
  }
  else
    return 0;
}

int EnQueue(QueuePointer queue,QueueDataType element){
  if(IsFull((*queue))){
    printf("the queue is over flow!\n");
    return 0;
  }
  queue->data[queue->tail]=element;
  ++(queue->tail);
  if(queue->tail==MAXQUEUESIZE)
    queue->tail=0;
  return 1;
}

心得：栈与队列，分别是两种FIFO和FILO的数据结构，至于具体实现，栈的增长和队列进出的方向完全可以由用户定义。另外，在实际的编程中，以循环队列的实现为例，容易出现逻辑错误的地方在于条件判断和边界条件的设定。其中条件判断要是充要条件，也就是说，你的代码需要能准确反应你的文字表述的意图，虽然我们设定的条件是队列满，但是如果用head=tail，虽然表示了队列满的情况，但是它也表示队列是空的情况，所以是不正确的。比如判断队列是满还是空，如果我们想要将数组的每个元素都利用，这时就会发现队列在满和空的时候满足同样的条件head=tail，显然，这是应该避免的；所以浪费了一个空间，来区分队列是满还是空这个情况。经验：行动前周密的思考能大量节省时间。

练习：编程实现2，4，5，6，7：

2，一个栈stack1从低地址到高地址，另外一个栈stack2从高地址到低地址：当top1>=top2时，栈溢出。

4，解答：参见本文中的代码，里面有对溢出情况的处理

5，解答：参见代码biqueue.c

6，解答：两个栈，栈底相连就是一个队列，但是要注意这两个栈为空的边界条件。

7，解答：两个队列，参考下图