海量数据挖掘——第1讲.MapReduce and PageRank
本栏目(数据挖掘)下海量数据挖掘专题是个人对Coursera公开课海量数据挖掘(2015)的学习心得与笔记。所有内容均来自Coursera公开课Mining Massive Datasets中Jure Leskovec, Anand Rajaraman以及Jeff Ullman老师的讲解。(https://class.coursera.org/mmds-002/lecture)
第1讲-------MapReduce and PageRank
一、Distributed File System
随着海量数据的I/O与计算需求越来越大,受到带宽与单个CPU计算能力有限的限制,原来的Singles Node Architecture(单CPU,单Memory以及单Disk)已经不能满足需求。这时传统的Cluster Architecture应运而生,如下图所示,用以解决大数据的存储与挖掘。
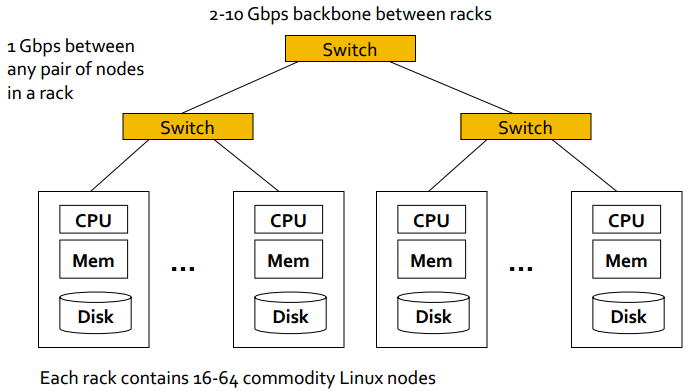
但是,传统的Cluster Architecture并没有完全解决问题,有如下的局限性:
- Node failures。假设单个server平均能持续1000天不fail,那么对于有1000台server的集群,平均每天1 node fail;1M台server的集群,平均每天1000 node fail。
- Network bottleneck。即使网络带宽是1Gbps,移动10TB的数据也要将近1天的时间。
- Distributed Programming is hard。分布式系统的复杂性。
MapReduce的出现就是为了解决传统Cluster Architecture的局限性。将数据冗余地存储在多个node上;Move computation close to data以减少数据的移动;提供Simple Programming Model影藏了分布式架构的复杂性。这三部分的内容都将会在接下来的内容中讲到。
其中第一个挑战的解决方案就是冗余存储架构,也就是经常提到的Distributed File System,例如Google GFS,Hadoop HDFS。它提供了全局的文件命名空间、冗余性以及可用性。典型的特点是Huge files;数据很少有update in place;常见的是数据的读取与文件末尾的添加。
Distributed File System的数据被切分成块chunks,每一个数据块都被复制多份保存在不同的machine上,这种情况下machine本身被称为chunk server。如下图所示,一个file被且分为C1-C6的数据块。chunk servers同时也扮演着compute servers的角色,这样就能实现Bring computation to data的目标。

总的来说,Distributed File System由如下的三部分组成:
- Chunk Server。文件被分成连续的chunk,大小为16-64MB;每一个chunk都会被复制多份(2x或者3x);将chunk的多份复制项保存在不同的rack中。
- Master node。其实也就是HDFS中的Name Node。保存了文件保存位置的metadata,例如文件被分为了6块以及所有数据块的具体位置。也有可能需要复制多份以防止Master node fail。
- Client Library for file access。当Chunk Server需要读取文件的时候,首先去查询Master node文件的metadata。当整整读取的时候则是通过Client Library直接读取文件,不需要再经过Master node。
二、 The MapReduce Computational Model
从经典的Word count的例子出发。假设有一个huge text document,需要统计其中distinct word出现的次数。对于Unix Shell来说,就是如下的一句命令:

这一条命令实际上已经道出了MapReduce用于word count的精髓。这三个步骤实际上都是可以并行化的,实际上也可以对应到MapReduce的如下三个过程。MapReduce的总体框架都是一样的,不同的问题只是Map和Reduce function相应的变化。具体的Map与Reduce的过程很简单,这里就不画图进行解释了。

那么更正式一点的来说,MapReduce Computational Model如下图所示。MapReduce的输入就是一系列的key-value对;Map就是对键值对进行映射;Reduce则针对相同的unique key进行需要的操作,然后输出结果。需要注意的是,当有多个reduce node的时候,map是通过hash函数讲相同的key放到同一个reduce函数上的。而且,使用的是sequence reading,节省时间。

三、 Scheduling and Data Flow
接下来,稍微深入一些MapReduce具体在分布式上的实现机制,如下图所示。实际上有多个nodes,每个node都有多个Map或者Reduce在运行。途中的Partitioning Function其实就是一个Hash Function,当有多个reduce node的时候,map是通过hash函数讲相同的key放到同一个reduce函数上的。这样的话可能会有多个key放到同一个reduce上,Group by key的操作就是针对key进行排序,分成多拨跑reduce函数。

所以Programmer只需要提供Map和Reduce两个函数,然后MapReduce环境承担了剩下所有的事情:将输入数据划分成块;调度程序在一系列的机器中运行;Map操作之后运行Group by key步骤;处理node会fail的情况;负责机器之间的通信等。所以从Data Flow的角度来说,Input和final output都存储在DFS上,Scheduler尝试让map task在输入数据块的chunk server上执行,bring computation to data。Map或者Reduce产生的中间结果都只保存在worker的local FS上,一个Map/Reduce对的输出往往是另一个Map/Reduce对的输入。
Master node主要负责task的调度。task分为idle,in-progress以及completed。当有空闲的worker时,idle task即准备执行。当Map task完成的时候,会将产生的R个中间文件的位置info发送给master,Master则负责将这些信息发送给各个reducer。Master node会周期性地ping每一个work确保他们没有fail。
当Map worker fail的时候,所有completed以及in-progress task都会被reset为idle,会被重新调度在别的worker上执行;当Reduce worker fail的时候,只有in-progress task会被重新调度在别的worker执行,因为Reduce的输出就是final output,它已经被写入到DFS中而不是local DFS中,所以completed task没必要重新调度执行。那如果Master fail呢?MapReduce task终止并且发出警告,Master node没有复制对于它fail的概率也很低。
那一般来说需要多少的Map和Reduce的job?M要比集群中的node数量大很多,每一个DFS chunk分配一个Map是很常见的,这样提高了动态负载平衡以及加速了worker failures的恢复。R一般比M要少,因为最终的输出是需要将R个输出文件集中起来的,所以少的数量会比较好。
四、 Combiners and Partition Functions
接下来介绍几个让MapReduce得以更高效率运行的改进。一个是Combiners。一个Map会经常产生大量的相同key的pair,例如在之前word count例子中的高频词汇。如果将这些Map产生的pair直接发送给Reduce,则需要大量的网络带宽损耗。Combiner的作用就是在每一个Mapper里将Map的输出结果进行一次结果的前期收集pre-aggregating,Combiner的操作usually和reduce function是一样的,如下图所示。

Combiner trick只有当reduce的运算满足交换律和结合律的时候才能有效,例如word count 中Sum的操作。有一些操作不能直接使用Combiner,不过对reduce的运算稍加调整之后可以使用,例如Average,如果reduce的操作是统计(sum,count)的二元组,最后进行average的计算。还有一些操作不管怎样都无法使用Combiner,例如Median求中位数。
另外一个是Partition Function。 Partition Function的存在就是为了让用户决定(key, value)的pair如何进入reduce worker。默认的partition function是hash(key) mod R,有时候想改变例如hash(hostname(URL)) mod R,希望来自同一个host的URL被分配到同一个reduce中去。
最早的MapReduce的实现是Google MapReduce,使用GFS作为stable storage,不开源;Hadoop是Google MapReduce的开源实现,使用HDFS作为文件系统;实践证明在Hadoop上面的数据操作很多都需要类似与SQL操作的数据处理,Hive和Pig则提供了基于Hadoop的SQL-like事务处理的抽象。另外云上的MapReduce最有名的要数Amazon‘s "Elastic Compute Cloud"(EC2),已S3作为文件系统。
五、 Link Analysis and PageRank
接下来,开始一个新的话题:Large Graph的分析。首先探讨Link Analysis方法,例如PageRank或者SimRank;其次也会探讨Community Detection,希望找出网络中节点的集群;然后我们也会研究Spam Detection。

Web也可以表示为一个有向图,每一个Webpage作为节点;超链接作为图的边。整个Web是一个巨大的有向图,那应该如何去Organize整个Web的内容呢?一种早期的方式就是人工地分类目录整理;另一种方式就是Web Search。但是,Web是庞大的,充满着大量的不可信文档,spam,不相关的信息等等。所以,Web search的两大挑战就是:一方面,Web上面的信息如何分辨哪些是可信的,一种trick就是可信的页面可能会指向彼此;另一方面,对于一个query(例如“newspaper”)哪一个结果才会是最好的结果,不会有单一的正确答案,一种trick认为知道newspaper的页面可能会指向很多newspaper。
还有一点,Web页面并不是同等重要的。我们希望计算出web graph中每个节点的重要性分数,依据就是link structure。link越多的节点,分数就越高。有很多方法来计算web graph中节点的重要性,它们统称为Link analysis。例如,PageRank,Hubs and Authorities(HITS)。另外,也会来看一些它们的扩展算法:Topic-Specific (Personalized) PageRank,Web Spam Detection Algorithms等。
六、 PageRank:The "Flow" Formulation
我们首先从直观上来感受下PageRank,也就是被称为The Flow Formulation,进一步地给出数学上的推导,然后具体地探讨它是如何计算重要性分数的。
直观上来说,它的核心思想就是Links as votes. 一个页面如果拥有越多的links,它就显得更重要。显然这里的links指的是in-coming links。与此同时,并不是所有的in-link都是同等重要,来自于重要性分数越高page的in-link更重要。对于一个page的所有out-link来说,它们平分这个page的importance score,如下图所示。


如上图所示的简单例子,利用高斯消元法就能够计算出每个page的重要性分数。但是对于大量的Web Graph,我们需要一个更好的方法。
七、 PageRank:The Matrix Formulation
为了利用线性几何来解决上节中提到的方程组解问题,我们需要重新从矩阵的角度重新来定义这个问题。引入邻接矩阵M,如下图所示,如果page i指向page j,那么M(j, i) = 1/d_i。这样的话,矩阵M中的每一列和都为1。同时定义向量r为所有page的重要性分数向量。

如何形象地理解这个Matrix Formulation?矩阵M中的第j行表示所有指向page j的in-link,矩阵M的第j行与向量r的内积即得到r_j。也即如上图的加和等式。然则,这个Matrix Formulation又解决了什么问题呢。
回忆一下线性代数中特征向量eigenvector与特征值eigenvalue的概念。对应任意一个square matrix A,如果满足下面等式:A * V = lambda * V(这里A是矩阵,V是向量,lamda是常数),我们就说V是A的eigenvector,lambda是A的eigenvalue。举个例子,如下图所示。对于一个矩阵可能有多个对应的eigenvector和eigenvalue。
简单对比即可发现,之前的Matrix Formulation的求解即是针对矩阵M在特征值为1时的特征矩阵r的求解。那么如果被给予一个矩阵M,要如何求解当eigenvalue=1时他的eigenvector呢?The Method is called Power Iteration.
八、 PageRank:Power Iteration
接下来,我们来看一下Power Iteration这个算法。假设整个Web Graph拥有N个节点,节点即网页page,边即为page之间的hyper link。如下图所示,这就是PageRank算法最简单的版本,我们从一个猜想的初始值开始,迭代大概50~100次,直到r收敛才认为得到了PageRank的重要性分数。

进一步地,我们来看看page rank score究竟代表着什么意思?这被称为Ramdom Walk Interpretation。我们将会看到page rank score将会等同于随机游走者ramdom web surfer在整个graph中行走的概率分布。在时刻t,surfer在节点i上;那么在时刻t + 1,surfer则会随机选择节点i的out-link走出下一步到达节点j,如此循环。
定义向量p(t),第i个元素代表surfer在时刻t时处于节点i的概率。也就是说,p(t)是一个各个页面节点之间的概率分布。那么,在时刻t+1时,the surfer又在哪里?

如上图所示,当the random walk达到平稳分布时p(t)是等同于p(t+1)的,也就是说我们之前要求解的特征向量r即为the random walk的平稳分布。所以,page rank score代表着random surfer随机游走中在给定的时刻t时位于特定节点的概率分布。随机游走在随机过程中也被称为马尔科夫过程。对于满足特定条件的graph来说,平稳分布是唯一的。也就说不管初始概率分布如何,最终都会到达同一个平稳分布的状态。
九、 The Google Formulation
上节我们讲到:对于满足特定条件的graph来说,平稳分布是唯一的。那么,究竟需要满足什么特定的条件?接下来我们讲探讨PageRank算法真正的Google Formulation版本。对于之前的Matrix Formulation等式,有几个遗留问题:
(1) 是否能收敛。考虑如下的“Spider trap”问题——所有的out-links都在一个group的内部,就会发现永远不会收敛。
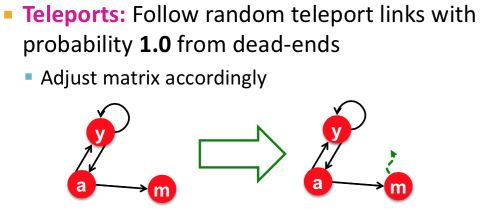
(2)是否能收敛到我们想要的程度。考虑如下的“Dead end”问题——某些page节点没有out-links,就会发现虽然收敛了但是不是我们想要的结果,Dead end节点会导致importance score“泄露”。
(3)结果是否是合理的。我们会发现以上的两大类问题得到的结果都是不合理的。
十、 Why Teleports Solve the Problem
这一节我们探讨一下为什么Teleports就能够解决之前PageRank算法的问题。回到之前马尔科夫链的理论,P(i, j)代表从节点j到节点i的概率。马尔科夫链的理论是说,对于任意的开始向量,Power Method使用马尔科夫变换P将会收敛到一个唯一的正稳态向量的充要条件是矩阵P是stochastic,irreducible以及aperiodic的。

接下来我们将会看到,加入Random Teleports的方案实际上某种程度上确保了变换矩阵P的这三种属性。
首先是Stochastic。矩阵是Stochastic的也就是说矩阵每列和加起来是1。对于“Dead Ends”的情况因为没有out-links,所以这一列的和加起来不是1而是0。但是当我们加入random teleportation的时候,我们就会发现加入了如下图所示的绿色箭头,这样的话就确保了矩阵M是Stochastic的。

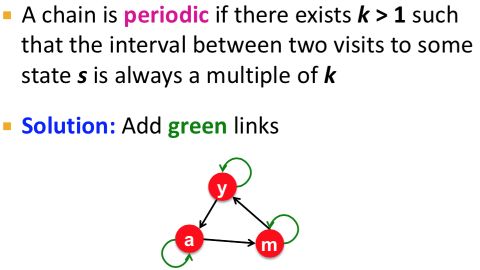
其次是Aperiodic。非周期性,如下图所示的循环链,random teleportation的加入相当于绿色links,保证了每两次访问某个节点的时间间隔是非周期性的。
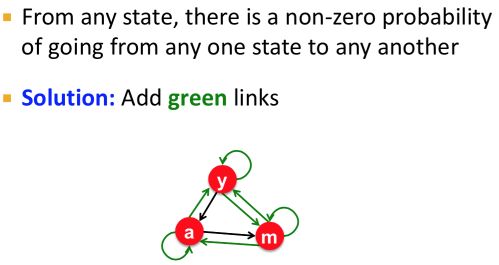
最后是Irreducible。对于任意的状态,从任一状态转换到另外任一状态的概率不能为0。
Google‘s 的解决方案解决了所有的这三个问题。也就是说,PageRank算法的Google Formulation如下图所示。

举个例子,这个时候的PageRank算法如何计算importance score的。
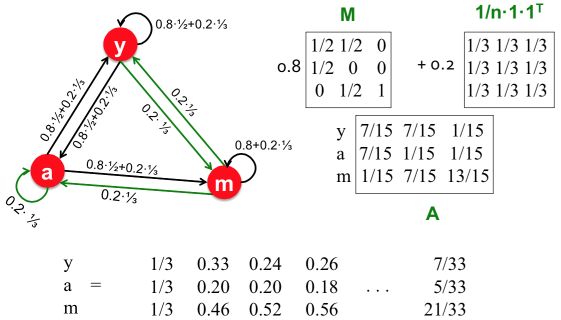
十一、 How we Really Compute PageRank
对于大规模的Web Graph,我们如何来计算PageRank score?当Web Graph大到内存不足以存下整个矩阵A的时候,该怎么办?

关于Mining Massive Datasets更多的学习资料将继续更新,敬请关注本博客和新浪微博Sheridan。
原创文章如转载,请注明本文链接: http://imsheridan.com/mmd_1st_lecture.html