poj 3565 Ants(几何调整思想)
|
Ants
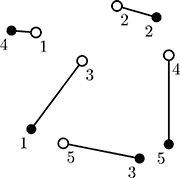
Description Young naturalist Bill studies ants in school. His ants feed on plant-louses that live on apple trees. Each ant colony needs its own apple tree to feed itself. Bill has a map with coordinates of n ant colonies and n apple trees. He knows that ants travel from their colony to their feeding places and back using chemically tagged routes. The routes cannot intersect each other or ants will get confused and get to the wrong colony or tree, thus spurring a war between colonies. Bill would like to connect each ant colony to a single apple tree so that all n routes are non-intersecting straight lines. In this problem such connection is always possible. Your task is to write a program that finds such connection. On this picture ant colonies are denoted by empty circles and apple trees are denoted by filled circles. One possible connection is denoted by lines. Input The first line of the input file contains a single integer number n (1 ≤ n ≤ 100) — the number of ant colonies and apple trees. It is followed by n lines describing n ant colonies, followed by n lines describing n apple trees. Each ant colony and apple tree is described by a pair of integer coordinates x and y (− 10 000 ≤ x, y ≤ 10 000 ) on a Cartesian plane. All ant colonies and apple trees occupy distinct points on a plane. No three points are on the same line. Output Write to the output file n lines with one integer number on each line. The number written on i-th line denotes the number (from 1 to n) of the apple tree that is connected to the i-th ant colony. Sample Input 5 -42 58 44 86 7 28 99 34 -13 -59 -47 -44 86 74 68 -75 -68 60 99 -60 Sample Output 4 2 1 5 3 Source
Northeastern Europe 2007
|
||||||||||
题目:http://poj.org/problem?id=3565
题意:给你n只蚂蚁和n棵树,每只蚂蚁和每棵树都有其自己的坐标,求每只蚂蚁对应一棵树,且路线不能相交
分析:首先初始化一个解,然后枚举两条边是否相交,相交就对调两棵树即可
代码:
#include<cstdio>
#include<iostream>
using namespace std;
const int mm=111;
typedef double diy;
struct point
{
diy x,y;
point(){}
point(diy _x,diy _y):x(_x),y(_y){}
}g[mm],h[mm];
struct segment
{
point s,t;
segment(){}
segment(point _s,point _t):s(_s),t(_t){}
};
point Vector(point s,point t)
{
return point(t.x-s.x,t.y-s.y);
}
diy CrossProduct(point P,point Q)
{
return P.x*Q.y-P.y*Q.x;
}
diy MultiCross(point P,point Q,point R)
{
return CrossProduct(Vector(Q,P),Vector(Q,R));
}
bool IsIntersect(segment P,segment Q)
{
if(max(P.s.x,P.t.x)<min(Q.s.x,Q.t.x)||max(P.s.y,P.t.y)<min(Q.s.y,Q.t.y)||
max(Q.s.x,Q.t.x)<min(P.s.x,P.t.x)||max(Q.s.y,Q.t.y)<min(P.s.y,P.t.y))return 0;
return (MultiCross(P.t,P.s,Q.s)*MultiCross(P.t,P.s,Q.t)<=0&&
MultiCross(Q.t,Q.s,P.s)*MultiCross(Q.t,Q.s,P.t)<=0);
}
int a[mm];
int main()
{
int i,j,n,ok;
while(~scanf("%d",&n))
{
for(i=1;i<=n;++i)
scanf("%lf%lf",&g[i].x,&g[i].y);
for(i=1;i<=n;++i)
scanf("%lf%lf",&h[i].x,&h[i].y);
for(i=1;i<=n;++i)a[i]=i;
while(1)
{
ok=1;
for(i=1;i<=n;++i)
for(j=1;j<=n;++j)
if(i!=j&&IsIntersect(segment(g[i],h[a[i]]),segment(g[j],h[a[j]])))
{
swap(a[i],a[j]);
ok=0;
}
if(ok)break;
}
for(i=1;i<=n;++i)
printf("%d\n",a[i]);
}
return 0;
}