Heterogeneous Parallel Programming(异构并行编程)学习笔记(六)
这里主要介绍CUDA的Overlapping计算。
1. Pinned Memory
所谓的Pinned Memory,是一种锁定内存物理地址的方法,对应于操作系统的分页技术。众所周知,操作系统的虚拟地址空间大于物理地址,通过分页(paging)技术来实现其转换与管理。如果在cudaMemcpy()过程中,正在发出或者接收数据的内存被paged out了,则对程序的性能肯定有影响。使用Pinned Memory能够避免这一问题。实际上,在调用cudaMemcpy(dest, src, ...)时,程序会自动检测dest或者src是否为Pinned Memory,若不是,则会自动将其内容拷入一不可见的Pinned Memory中,然后再进行传输。可以手动指定Pinned Memory,对应的API为:cudaHostAlloc(address, size, option)分配地址,cudaFreeHost(pointer)释放地址。注意,所谓的Pinned Memory都是在Host端的,而不是Device端。
2. Overlapping
部分的CUDA设备支持Overlap特性,使I/O和计算能够并行处理。这种特性能够更加优化程序性能。
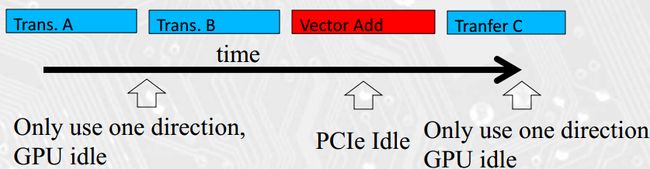
何为Overlapping?以向量相加为例,一个简单的向量加法的处理过程可能如下所示:
从上图中可以很清楚地看到,在同一设备的同一时间,只有一种操作在进行,而其它资源处于闲置状态。
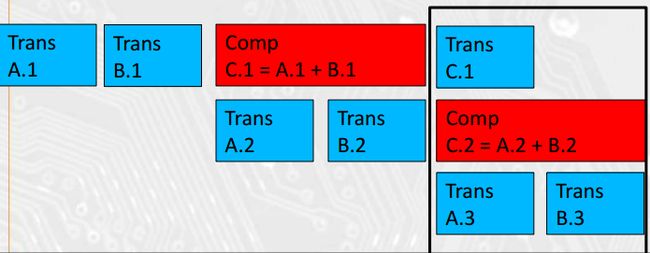
让设备在I/O的同时计算,就是一个Overlapping的例子。注意到计算过程对I/O存在依赖,我们可以把I/O拆分为很多块,一个理想的Overlapping计算模型应该如下所示:
从第三个输入块开始,设备就是以一种理想的Overlapping方式在运行。可以把设备处理的方式想象为三个流:输入流,计算流,输出流。输入流首先开始执行;在执行完第一分块后,计算流开始执行;在计算流执行完第一分块的计算后,输出流开始执行。在最理想情况下,如果计算一个分块的时间与输入一个分块的时间相等,且不大于输出一个分块的时间,则三个流可以不受阻隔地运行下去。但事实肯定不会如此,所以流之间的同步是必须的,每一个分块的执行时间取决与该分块执行最慢的流。
3. Overlapping实现
CUDA也是用流的概念来实现Overlapping,不过编程实现时和上述内容有一些不一致。以向量相加为例:
// create two streams
cudaStream_t stream0, stream1;
cudaStreamCreate( &stream0);
cudaStreamCreate( &stream1);
// device memory for both streams
float *d_A0, *d_B0, *d_C0;
float *d_A1, *d_B1, *d_C1;
// do calculation
for (int i=0; i<n; i+=SegSize*2) {
cudaMemCpyAsync(d_A0, h_A+i; SegSize*sizeof(float),.., stream0);
cudaMemCpyAsync(d_B0, h_B+i; SegSize*sizeof(float),.., stream0);
cudaMemCpyAsync(d_A1, h_A+i+SegSize; SegSize*sizeof(float),.., stream1);
cudaMemCpyAsync(d_B1, h_B+i+SegSize; SegSize*sizeof(float),.., stream1);
vecAdd<<<SegSize/256, 256, 0, stream0)(d_A0, d_B0, …);
vecAdd<<<SegSize/256, 256, 0, stream1>>>(d_A1, d_B1, …);
cudaMemCpyAsync(d_C0, h_C+I; SegSize*sizeof(float),.., stream0);
cudaMemCpyAsync(d_C1, h_C+i+SegSize; SegSize*sizeof(float),.., stream1);
}
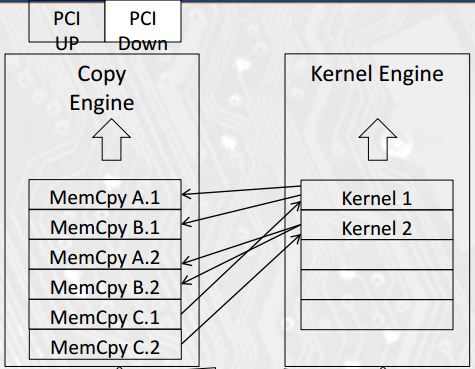
上面通过cudaStreamCreate()建立了两个流,并在for循环中给每个流分配了任务。其中的cudaMemcpyAsync()是cudaMemcpy()用于Overlapping的版本,意味着在传输内存内容时不需要停止内存上的计算。上述代码的执行情况如下图所示:
CUDA用两个队列来维护操作,也就是图中的两个Engine。在MemcpyA.1和MemcpyA.2执行后,MemcpyA.2和Kernel1会同时开始执行,从而达到了Overlap的效果。但需要注意的是,上述的代码并没有完整地实现Overlapping,而仅在每一次循环内部实现了Overlapping。完整地实现需要三个流和更为复杂的控制。