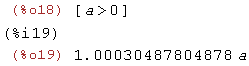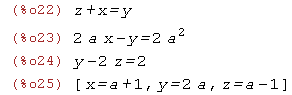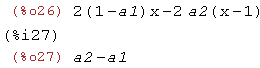maxima 代数方程求解

本文最初写于 2010-07-21 于 sohu 博客，这次博客搬家一起搬到这里来。

版权所有，转载请注明出处。

一般的代数方程

solve (expr, x)
solve (expr)
solve ([eqn_1, ..., eqn_n], [x_1, ..., x_n])

几个例子：

solve (asin (cos (3*x))*(f(x) - 1), x);

[4*x^2 - y^2 = 12, x*y - x = 2];
solve (%, [x, y]);

多项式方程

realroots 计算多项式方程的数值解.

realroots (expr, bound)
realroots (eqn, bound)

realroots (expr)
realroots (eqn)

几个例子：

realroots (-1 - x + x^5, 5e-6);
realroots (expand ((1 - x)^5 * (2 - x)^3 * (3 - x)), 1e-20);

allroots 计算多项式方程的全部解.

allroots (expr)

allroots (eqn)

几个例子：

eqn: (1 + 2*x)^3 = 13.5*(1 + x^5);
soln: allroots (eqn);

二分法求数值解

find_root (expr, x, a, b)
find_root (f, a, b)

几个例子：

find_root (sin(x) - x/2, x, 0.1, %pi);

find_root (sin(x) = x/2, x, 0.1, %pi);

f(x) := sin(x) - x/2;
find_root (f(x), x, 0.1, %pi);

牛顿迭代法

newton (expr, x, x_0, eps)

mnewton (FuncList,VarList,GuessList)

newton 用来解方程，mnewton 用来解方程组

几个例子：

load (newton1)$
newton (cos (u), u, 1, 1/100);

assume (a > 0);

newton (x^2 - a^2, x, a/2, a^2/100);

load("mnewton")$
mnewton([x1+3*log(x1)-x2^2, 2*x1^2-x1*x2-5*x1+1], [x1, x2], [5, 5]);

 

线性代数方程组

linsolve ([expr_1, ..., expr_m], [x_1, ..., x_n])

几个例子：

e1: x + z = y;
e2: 2*a*x - y = 2*a^2;
e3: y - 2*z = 2;
linsolve ([e1, e2, e3], [x, y, z]);

多项式方程组

algsys ([expr_1, ..., expr_m], [x_1, ..., x_n])
algsys ([eqn_1, ..., eqn_m], [x_1, ..., x_n])

几个例子：

e1: 2*x*(1 - a1) - 2*(x - 1)*a2;
e2: a2 - a1;

e3: a1*(-y - x^2 + 1);
e4: a2*(y - (x - 1)^2);
algsys ([e1, e2, e3, e4], [x, y, a1, a2]);