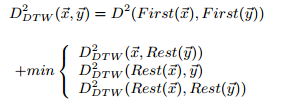动态时间规整DTW简述
动态时间规整是一种用于对齐向量,并计算最小距离的算法,个人感觉其思想和LCS十分类似。
同样,设两个向量为x,y,First(x)表示x的第一个元素,Rest(x)表示除第一个元素以外的x的剩余元素组成的向量
采用欧氏距离作为距离度量,即向量间的距离用对应元素的平方和再开根号表示,即:
D(A,B) = sqrt [ ∑( ( a[i] - b[i] )^2 ) ] (i = 1,2,…,n)
用D(x,y)表示x,y的DTW距离
定义:两个向量x,y的DTW距离为:
思路:设x长度为n,y长度为m,搜索过程就是在n*m的网格中寻找一条路径,使路径所经过的点对应的x[i],y[j]的距离的平方和最小。
每次搜索时,先计算当前网格中的x[i],y[j]的距离的平方,然后向网格x轴,y轴和对角线三个方向递归搜索,寻找距离最小的路径。
类似LCS,DTW也可以用动态规划方便的实现,搜索空间为n*m
设dp[i][j]表示以x[i]和y[j]开始的子序列的DTW距离,则递归方程为:
dp[i][j] = (x[i]-y[j])^2 + MIN(dtw(i+1,j+1),dtw(i+1,j),dtw(i,j+1))
注意递归边界,先将搜索终点dp[n-1][m-1]赋值。
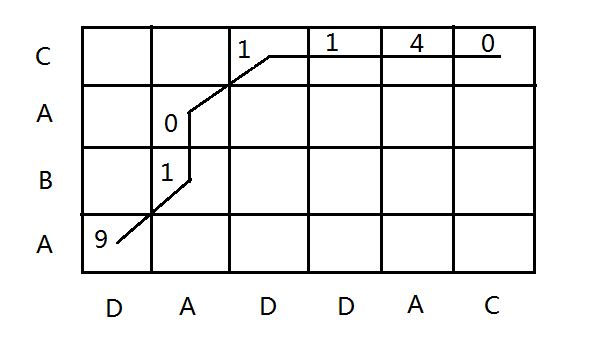
例:给定x="ABAC",y="DADDAC"
匹配路径如下图所示:
每个网格的数字表示路径在该点增加的距离的平方,由图所示,D^2(x,y)=16
代码如下:
#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
using namespace std;
const int maxn = 100;
const int maxv = 1000000;
string a,b;
int n,m;
int dp[maxn][maxn];
int MAX(int x,int y)
{
return x>y?x:y;
}
int MIN(int x,int y)
{
return x<y?x:y;
}
int dtw(int i, int j)
{
if(i>=n || j>=m)
return maxv;
if(dp[i][j]>=0)
return dp[i][j];
dp[i][j] = (a[i]-b[j])*(a[i]-b[j]) + MIN(dtw(i+1,j+1),MIN(dtw(i+1,j),dtw(i,j+1)));
return dp[i][j];
}
int main()
{
a = "ABAC";
b = "DADDAC";
n = a.length();
m = b.length();
memset(dp,-1,sizeof(dp));
dp[n-1][m-1] = (a[n-1]-b[m-1]) * (a[n-1]-b[m-1]);
cout<< dtw(0,0) << endl;
for(int i=0; i<n; i++)
{
for(int j=0; j<m; j++)
cout<<dp[i][j]<<" ";
cout<<endl;
}
}