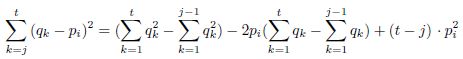A Top-down Approach to Melody Match in Pitch Contour for Query by Humming

原文下载：http://www.mirlab.org/conference_papers/International_Conference/ISCSLP%202006/pdfs/B66.pdf

翻译论文1,2,3,5章，主要介绍的递归对齐RA算法及其变形，不得不说中科院的文章把挺简单的一个算法整的复杂冗长……有时间会单写一个RA简单版

翻译中标注了一些不明白的地方，也欢迎高手指正~

 

一种自顶向下的用于哼唱检索的音高曲线旋律匹配方法

——递归对齐（RA）

 

 

摘要：本文提出一种新的基于帧的算法——递归对齐（RA），用于哼唱检索（QBH）系统。相比于其他方法，RA用自顶向下的方式优化了旋律对齐的问题，能更有效的捕捉人哼唱时的长距离信息。三种RA的变形模式能够在损失一定精度的情况下大幅提高速度，能够用作QBH系统的滤波器。本文简要描述了一个基于RA和其变形的QBH系统。实验结果表明，该算法与其他已经实现的算法相媲美。

 

1背景介绍

 

目前的哼唱检索系统分为两种：基于音符和基于帧的。大多数研究都关注基于音符的QBH系统。基于音符的系统中，先将音高序列切分为音符，然后用某种方法在数据库中找到最相似的匹配。定义一种距离度量后，近似串匹配方法通常被用来计算候选对于查询的得分。另一种对齐序列的方法是HMM的维特比解码算法。Meek and Brimingham的用HMM框架对QBH的错误建模，能抵消很多类型的切分错误和哼唱错误。换句话讲，就是一些研究人员认为不可靠的音符切分是限制基于音符的QBH系统性能的主要因素，而数据库中歌曲的装饰音也会使匹配结果变差，所以研究集中于在帧的层面将查询和候选直接对齐。该领域的先驱者J.Jang用两级DTW在800首歌的曲库上实现了78%的top-1准确率，是当时同类研究中最高的。Mazzoni and Dannenberg指出了基于音符方法的缺陷。也有研究人员对比了三种最常用的旋律匹配算法的性能，分别是基于音符的串匹配，基于音符的HMM下的维特比解码和基于帧的DTW。

 

上述所有提到的研究中，查询与候选间的匹配得分的计算用的都是自底向上的方法。由于在数学上要保证全局最优解，几乎所有QBH系统，无论基于音符还是基于帧的，都选用基于基于DP的方法作为最后一级的匹配算法，如最长公用子串LCS，维特比解码和DTW。DP是一种典型的自底向上最优化解法，通过利用子问题的解得到全局的解。但是在音乐检索中，查询和候选的相似度不仅依赖于局部匹配得分的累计，也依赖于全局曲线的匹配。像持续时间和节奏这种长距离信息，用自底向上的方法很难捕获到。J.Jang用线性缩放（LS）方法的结果就比维特比解码要好。他们的工作是首次在最后一级计算得分时抛弃了自底向上方法。然而，LS比较粗糙，只在用大量数据训练后的模型上才能有良好的性能。

 

本文提出一种新的基于帧的旋律匹配算法——递归对齐（RA）。RA由LS启发得到，并且消除了LS的限制。RA是一种自顶向下的算法，首先在全局层面尝试匹配查询和候选，然后再进行局部调整。RA通过递归方式优化对齐问题，直接计算出音高曲线的匹配得分，而不需要进行训练。此外，本文提出三种RA的变形，能够在损失一定精度的情况下大幅提高速度，能够用作QBH系统的滤波器，来高效的滤除大部分不可靠候选。本文还描述了基于RA及其变形的QBH系统。该系统使用8级滤波，从百万量级的旋律中选取600个最有可能的旋律片段。虽然一些滤波器用到一些基于音符切分的原理，但是整个系统并不依赖于此。设计滤波器时，以自顶向下为原则，系统倾向于选取全局特征而非局部的。最终的实验结果显示，系统能实现83.77%的top1检索正确率，每个查询的处理时间为3.3秒。

 

第2章描述了现有技术和RA算法，第3章讲述了3种RA变形，第4章描述了基于RA的QBH系统，给出系统实验结果。

 

2帧层面的旋律匹配

 

这一章主要介绍基于帧的音乐检索系统的额匹配方法。2.1定义问题，2.2简要介绍了现有的基于帧的匹配算法，如DTW和LS，2.3详细阐述本文提出的方法。

 

2.1问题定义

 

在基于帧的QBH系统中，首先将哼唱按帧处理，输出音高序列，并转换为半音音阶。本文中，半音音阶的音高序列标记为(q1,q2,…,qn)。然后开始搜索候选得到候选集，考虑到匹配的效率，建立索引和滤波，用来减少候选。上述过程完成后，得到候选集(C1,C2,…,CN)，每一个候选都由一些音符组成，表示为((p1,d1),(p2,d2),...,(pm,dm))，其中，pi和di分别表示第i个音符的音高和持续时间。

 

有了上述符号，旋律匹配的问题定义为：给定查询的帧序列Q=(q1,q2,…,qn)，音符序列N=((p1,d1),(p2,d2),…,(pm,dm))和距离函数dist(q,(p,d))，如何计算两个序列之间的匹配得分S。一般情况下，最优的或次优的对齐得分作为匹配得分。只要这样一个旋律匹配算法可以实现，那么就能通过对所有候选的得分排序，找到top-N候选。

 

2.2现有的基于帧的匹配算法

 

2.2.1 DTW

 

DP常用做QBH系统的最终排序算法。其中，DTW就是一种基于帧的算法，寻找最优的对齐路径。DTW中，根据音符的持续时间，候选N被扩展为帧序列N’=(p1’,p2’,…,pl’)。Dij表示查询的第i帧和候选的第j帧的最小累计距离，用下式计算：

时间复杂度O(nl)。

 

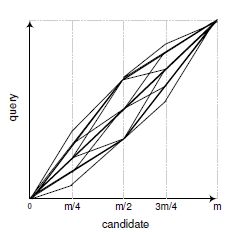
然而，DTW在找最优解时可能会忽略全局结构。例如，图1中，每条线代表一条对齐路径，l1和l2明显比l3和l4更合理，这是以哼唱者不会频繁变化节奏为前提。这种信息通常很难，或者需要花费很大代价才能被DP捕捉到。即使很多DTW变形已经在捕捉长距离结构上有更好的表现，但是自底向上框架的本质限制了DTW的性能。

图1查询和候选对齐路劲示例

 

 

2.2.2 LS

 

LS是另一种旋律匹配方法，只需O(n)时间。不像DTW通过局部解得到全局解，LS只选择l1（见图1）作为对齐路径。虽然LS看上去很粗糙，但是J.Jang的研究表明，它的性能比基于HMM的维特比解码方法还要好。LS的缺陷很明显：局部的节奏不匹配会影响全局匹配结果，并且需要训练才能捕捉哼唱的习惯。算法过程如下：

算法实现的是把Q线性映射到N对应位置，并计算距离

Dura：N的总帧数

Dist：计算距离

Scale：N的一帧对应Q的多少帧

每次循环遍历一个N的音符pi，找到pi对应Q的帧范围[j,t]，计算这个范围内的qk与pi的距离，累计计入Dist

返回距离Dist的负值

 

2.3新的自顶向下的匹配算法

 

本文提出的新算法递归对齐（RA）描述如下图，RA来源于LS，并消除了LS的限制。该算法不同于DP之处在于从全局角度求最优解。不同于LS之处在于递归调整局部匹配，以优化对齐。

Q：查询，qi为每帧的音符，n为帧数

N：候选，(pi,di)为音符和持续时间，m为音符数

S：缩放因子对，(sxi,syi)为两部分的缩放因子

D：递归深度

J：音符数的一半

Sc：前一半音符持续时间的比例（若前半段音符持续时间短，那么音符中点j不是时间中点）

N1,N2：以音符数切分的N的两半

每次循环遍历S中的一个缩放因子对(sx,sy)

K：N1在缩放因子sx下对应的Q的前半段帧数

Q1,Q2：缩放因子sx,sy下Q的两半

Score：Q1，N1和Q2，N2的LS距离和

MaxScore：记录最大距离值，由于LS返回距离的负值，实际上记录的是最小距离

i：距离最大距离时的切分点，即Q前半段帧数

若D=0，返回距离，否则，递归计算Q1，Q2的距离

 

RA的基本思想来源于查询和候选相似当且仅当它们整体形状大致相同时。通常从查询到候选的最优对齐时一个非线性的变换。这个变换可以近似为，将候选分钟两部分，每部分进行线性缩放。两部分近似最优的缩放因子能通过暴力搜索得到，也就是说，给定一组可能缩放因子对{(sx1,sy1),(sx2,sy2),…,(sxn,syn)}，计算每对缩放因子，找出计算距离最小的一对作为结果。高层的缩放因子对选好后，整体对齐问题就变成两个子串的对齐问题，可以同样用上述方法求解。注意，在RA优化过程中，先计算高层再计算底层，这样对齐问题就能用自顶向下递归的方式求最优解。图2给出了优化过程的例子。

RA实际上是用分段折线去近似DTW所算出的最佳曲线路径，其时间复杂度大大低于DTW，但是用折线近似曲线得到的不是最优解，只是近似最优。换句话说，就是用损失一定精度的代价加快算法速度。

图2 RA示例（|S|=3,D=1）。粗线，细线和虚线分别表示当前层的实际路径，最佳路径和舍弃路径

 

如在算法2中所示，RA将LS作为子程序。需要注意的一点是LS中用到的函数dist(q,p)是：

Dist(q,p) = min{(q-p)^2,floor}

 

Floor是一个预定义常数，用来限制任一对齐对(q,p)的贡献度。研究显示floor的引入大幅提升了算法的性能。其原因可能是，用式y=∑(x^2)计算欧氏距离时，不匹配的对的比重比匹配的比重要大很多，引入floor减小了单个对的影响。

 

从图搜索的角度分析RA。虽然RA是根据之前的切分点动态扩展搜索空间，但是在Q,N,S,D已知的情况下，整体搜索图是确定的。如图3所示，每个路径都是2^(N+1)分支的折线，N即候选长度。只要S合适，图1中的l3,l4路径不会出现，先置定高层切分点将局部的调整限制在一个合理的范围内。在搜索图中，RA可以看做一个带有全局剪枝策略的启发式搜索。一个更吸引人的步骤是用经典的自左至右的算法如DP去搜索RA生成的搜索图，结合了找到最佳路径的优点，并用人哼唱的习惯限制了搜索。然后，下文的实验结果显示，纯RA性能稍好于混合算法，表明了RA剪枝策略的十分有效。

图3 RA搜索空间（|S|=3,D=1）

 

3 RA变形

 

介绍3种RA的变形，目的是用一些精度损失使算法更快。QBH系统中，将这些变形用于滤波，高效的滤除大部分伪候选。由于RA的瓶颈是LS的帧间距离计算，所以前两个变形是将LS用于音符间距离的计算，而第三个变形是并行计算若干帧的距离。

 

3.1 变形1

 

这个变形在音符层面计算LS距离。算法1中帧层面的距离和计算了所有和第i个音符对齐的查询片的帧，这个式子可以改写为：

注意：pi为候选N的第i个音符，pi对应查询Q的帧范围为[j,t]，上式即把(qk-pi)^2展开，再把qk^2和2qk分别展开成两项，把pi单独提出来。

 

此时忽略了floor参数。如果已经预先计算了对所有l的，那么上式的结果可以很快解出。这个方法由Viola在人脸检测中用到的一个类似的避免重复计算的方法启发而来。该方法将时间复杂度从O(kn)降到O(km)，其中n为查询的帧数，m为候选的音符数，且m<<n。该方法的缺点就是，因为忽略的距离上界参数floor，上文提到的单个点问题可能会降低系统性能。（该式为何不引入floor？）

 

3.2 变形2

 

第二个变形同样在音符层面计算LS，不同的是用了音符分隔的信息。虽然音符切分容易错误，但是这种变形对切分错误不敏感。设查询Q被切分为r个音符((p1’,d1’),(p2’,d2’),…,(pr’,dr’))，用音符间RA算法计算匹配的得分。要计算查询(p’,d’)和候选(p,d)之间的距离，时间复杂度为O(m+r)。上面的距离上街参数floor也可以被考虑进来。该方法的缺点是，将实数值的帧量化为音符时，信息有丢失，造成精度下降。

 

3.3 变形3

 

第三个变形不同于前两个。首先将频率划分为b个子带，将每帧在每个子带量化为0或1，如图4所示。计算每个子带的RA距离，最终得分是所有子带得分的和。这个变形的目的在于避免大量的浮点数计算，并使得分能够在一般32位计算机上并行计算。时间复杂度为O(kbn/32)，b为子带数，n为音符数。该方法的缺点是，在二值化时丢失了大量信息。

图4 RA变形3

 

5 结论

本文提出了一种新的基于帧的音乐检索算法——递归对齐（RA）。与现有方法相比，RA用自顶向下的方式优化了旋律对齐问题，捕捉到了哼唱中的长距离信息。本文也提出了三种RA变形，在损失少量精度的情况下大幅提高速度，用作QBH系统的滤波器。从哇哦，本文简要描述了基于RA和其变形的QBH系统。本文认为旋律匹配应从全局角度开始，我们的实验也支持了这个观点。