改进的模拟退火求TSP问题(二)
上篇已经写一段基于matlab模拟退火求解TSP问题,对其中的原理基础有一定的解释,该篇是对上次的问题进行一定的改进与优化。
上篇算法核心中,只是用到了模拟退火中最简单的方式对问题进行求解。然而改进的方式很多,对模拟退火算法的改进,可通过增加某些环节而实现。主要的改进方式包括(可参考具体文献解释:一种改进的模拟退火算法,朱颢东、钟勇):
(1)增加升温或重升温过程。在算法进程的适当时机,将温度适当提高,从而可激活各状态的接受概率,以调整搜索进程中的当前状态,避免算法在局部极小解处停滞不前。
(2)增加记忆功能。为避免搜索过程中由于执行概率接受环节而遗失当前遇到的最优解,可通过增加存储环节,将“Best So Far”的状态记忆下来。
(3)增加补充搜索过程。即在退火过程结束后,以搜索到的最优解为初始状态,再次执行模拟退火过程或局部趋化性搜索。
(4)对每一当前状态,采用多次搜索策略,以概率接受区域内的最优状态,而非标准SA的单次比较方式。
(5)结合其他搜索机制的算法,如遗传算法、混沌搜索等。
而在该篇中,主要是通过重升温、控制交换点数目、记录最优解这几种方式来进行的。主要也是修改上篇中的simulatedannealing函数来实现。在这个过程中,搜到了一篇比较好的文献(SIMULATED ANNEALING FOR TRAVELING SALESMAN PROBLEM),该篇也借鉴了其中的部分程序编写方式。具体修改后的程序如下所示:
%-------------函数说明----------------
% 模拟退火函数
% 输入变量:
% inputcities:原来的地点顺序和位置
% initial_temperature:初始温度
% cooling_rate: 降温比例系数
% threshold : 一个循环次数
% numberofcitiestoswap : 每次交换地点的对数
%---------------------------------------
function simulatedannealing(inputcities,initial_temperature,...
cooling_rate,threshold,numberofcitiestoswap) %退火算法
global iterations; %全局变量--迭代次数--作为循环条件
iterations = 1;
number_interations = 0; %定义一个迭代次数用于降温操作
best_cities = inputcities ; %用于记录已经找到的最好解
best_distance = distance(best_cities);
num2swap_change = 0; %定义一个变量--交换城市数目
tempeature = initial_temperature; %初始温度
input_cities = inputcities; %城市坐标
%while tempeature > 0.01 %循环条件,把降温底线作为条件
while iterations < threshold %新的循环条件--迭代次数
num2swap_change = num2swap_change + 1;
previous_distance = distance(input_cities); %旧距离和
temp_cities = swapcities(input_cities,numberofcitiestoswap); %随机n次交换
current_distance = distance(temp_cities); %新距离和
diff = abs(current_distance - previous_distance); %产生误差
%-------------------------解变好的情况---------------------------
if current_distance < previous_distance %距离变少了,直接接受,不用考虑
num2swap_change = 0; %进入循环后该变量清0
input_cities = temp_cities; %接受
%---------记录最好的解--------------
if best_distance > current_distance
best_cities = input_cities;
best_distance = distance(best_cities);
end
%----------------------------------
if number_interations >= 5
tempeature = tempeature*cooling_rate; %降温过程
number_interations = 0;
end
numberofcitiestoswap = round(numberofcitiestoswap*exp(-diff/(iterations*tempeature)));
if numberofcitiestoswap == 0
numberofcitiestoswap = 1;
end
iterations = iterations +1 ;
number_interations = number_interations + 1;
%---------------------解不好的情况---------------------------
else
if rand(1) < exp(-diff/(tempeature)) %否则,以一定的概率接受
num2swap_change = 0;
input_cities = temp_cities; %概率符合了,进来接受
numberofcitiestoswap = round(numberofcitiestoswap*exp(-diff/(iterations*tempeature)));
if numberofcitiestoswap == 0
numberofcitiestoswap = 1;
end
iterations = iterations +1 ;
number_interations = number_interations + 1;
end
end
%--如果一直循环着没有进入if中,就得改变条件让其进入if中-----
if num2swap_change > 100
input_cities = best_cities; %--把最好解转到input_cities中
tempeature = tempeature/0.951; %升温--使其进入循环概率变大
if numberofcitiestoswap > 1 %交换城市数降到1对时停止
numberofcitiestoswap = numberofcitiestoswap - 1;
if numberofcitiestoswap == 0
numberofcitiestoswap = 1;
end
num2swap_change = 0;
end
end
end
fprintf('\t\t\tTempeature = %3.8f\n',tempeature); %输出结果
current_distance = distance(input_cities);
fprintf('\t\t\tFinal_istance = % 3.8f best_dis = % 3.8f\n',current_distance,best_distance);
plot(best_cities(1,:),best_cities(2,:),'*');
hold on,plot(best_cities(1,:),best_cities(2,:));
可以看到,相对上篇,还是添加了一些内容。改变了循环条件,以迭代次数作为结束的条件,同时增加了较多的中间变量。对于中途中升温的方式以及后面的重升温来跳出局部最优解的方式也改变了下。这个过程中也存储了所有的整个过程中的最优解。程序的模式没有太大的改变,只是加了一些改变元素在其中,详细的标注在程序中,应该不难理解。
当然,这个改进还是对结果有一些优化作用的。由于模拟退火算法的随机性,每次的结果是不一样的,而且深受参数的影响。这里我在不断改变参数的基础上得出了其中几次的较好解如下:
simulatedannealing(cities1,1,0.9,1000,20),得到的结果如下:Final_istance = 5.02695718

>> simulatedannealing(cities1,1,0.94,3500,15)
best_dis = 5.00124640
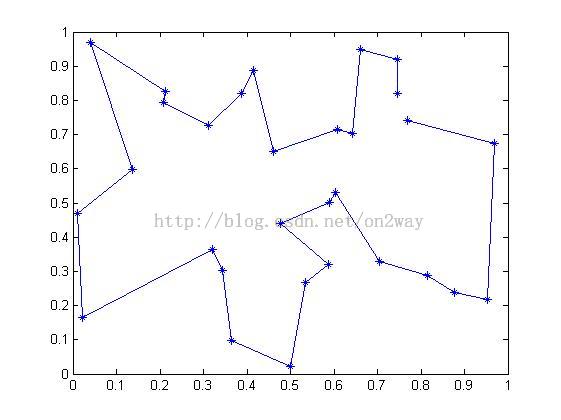
当然,这还不是最好解,有一次结果达到了4.997左右,图没有记录上,遗憾了。再运行的话解也始终在5左右了。
总的看来,改进的算法还是有一点用的,起码每次都能把结果优化到一个较好的水平了。当然,感觉模拟退火还是有比较多的缺陷,受参数影响大,更适用于局部搜索,如果能和其他算法结合着使用相信能有更好的结果吧,想多了解,去看文献吧。