Hermite多项式
http://blog.csdn.net/pipisorry/article/details/49366047
Hermite埃尔米特多项式
在数学中，埃尔米特多项式是一种经典的正交多项式族，得名于法国数学家夏尔·埃尔米特。概率论里的埃奇沃斯级数的表达式中就要用到埃尔米特多项式。在组合数学中，埃尔米特多项式是阿佩尔方程的解。物理学中，埃尔米特多项式给出了量子谐振子的本征态。
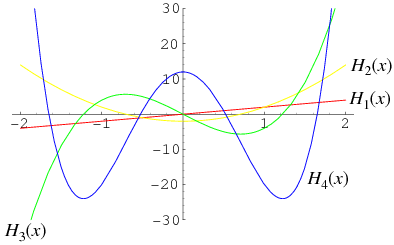
前4个（概率论中的）埃尔米特多项式的图像
The Hermite polynomials 
are set of orthogonal polynomials over the domain
with weighting function
, illustrated above for
, 2, 3, and 4. Hermite polynomials are implemented in the Wolfram Language asHermiteH[n,x].
The Hermite polynomial 
can be defined by the contour integral
 |
(1)
|
where the contour encloses the origin and is traversed in a counterclockwise direction (Arfken 1985, p. 416).
Hermite多项式，其正交域为(-∞, +∞)，其一维形式是
前10个Hermite多项式
H_0(x) = 1
H_1(x) = 2x
H_2(x) = 4x^2-2
H_3(x) = 8x^3-12x
H_4(x) = 16x^4-48x^2+12
H_5(x) = 32x^5-160x^3+120x
H_6(x) = 64x^6-480x^4+720x^2-120
H_7(x) = 128x^7-1344x^5+3360x^3-1680x
H_8(x) = 256x^8-3584x^6+13440x^4-13440x^2+1680
H_9(x) = 512x^9-9216x^7+48384x^5-80640x^3+30240x
H_(10)(x) = 1024x^(10)-23040x^8+161280x^6-403200x^4+302400x^2-30240
The values 
may be called Hermite numbers.When ordered from smallest to largest powers, the triangle of nonzero coefficientsis 1; 2; -2, 4; -12, 8; 12, -48, 16; 120, -160, 32; ... (OEISA059343).
Hermite多项式的性质
多项式Hn 是一个n次的多项式。概率论的埃尔米特多项式是首一多项式（最高次项系数等于1），而物理学的埃尔米特多项式的最高次项系数等于2n。
正交性
多项式Hn 的次数与序号n 相同，所以不同的埃尔米特多项式的次数不一样。对于给定的权函数w，埃尔米特多项式的序列将会是正交序列。
- （概率论）
- （物理学）
也就是说，当m ≠ n 时：
除此之外，还有：
- （概率论）
- （物理学）
其中是克罗内克函数。
从上式可以看到，概率论中的埃尔米特多项式与标准正态分布正交。
完备性
在所有满足
的函数所构成的完备空间中，埃尔米特多项式序列构成一组基。其中的内积定义如下：
埃尔米特微分方程
概率论中的埃尔米特多项式是以下微分方程的解:
方程的的边界条件为：应在无穷远处有界。
其中是这个方程的本征值，是一个常数。要满足上述边界条件，应取∈。对于一个特定的本征值，对应着一个特定的本征函数解，即。
而物理学中的埃尔米特多项式则是以下微分方程的解:
其本征值同样为∈，对应的本征函数解为。
以上两个微分方程都称为埃尔米特方程。
from: http://blog.csdn.net/pipisorry/article/details/49366047ref:mathworld Hermite Polynomial
wikipedia 埃尔米特多项式