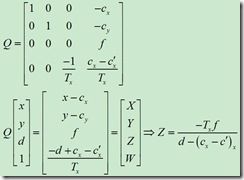Matlab摄像机标定和立体标定
1. 摄像头
我用的摄像头是淘宝上买的三维摄像头,两个USB Camera加一个可调节的支架。实物照片如下
1.1 三维摄像头实物图
双USB摄像头的OpenCV驱动可以参考以下链接
http://www.opencv.org.cn/index.php/使用DirectShow采集图像
将上面代码复制到自己的工程之后还需要对工程或者编译环境做一下设置
VC6下的详尽设置可以见代码的注释(修改工程的属性)
VS2008中的设置也可以参照代码注释中VC++2005的设置(修改编译环境)
2. 标定
由于OpenCV中cvStereoCalibrate总是会得到很夸张的结果(见下文5.1问题描述),所以最后还是决定用Bouguet的Matlab标定工具箱立体标定,再将标定的结果读入OpenCV,来进行后续图像校准和匹配。
Matlab标定工具箱的参考链接如下:
http://www.vision.caltech.edu/bouguetj/calib_doc/
上面有详细的使用步骤,用起来相当的方便。
以下是我个人用Matlab工具箱进行立体标定的步骤,供参考,如果需要更详细步骤的话还是参照上面的链接
把Matlab工具箱的文件copy到对应目录下,把所要标定的棋盘图也放到.m文件所在的目录下,然后在Matlab命令行窗口中打入calib_gui,选择Standard之后便出现以下窗口
2.1. calilb_gui面板
我们先对右摄像头的标定,所以先把从右摄像头上采集到的棋盘图复制到工具箱目录下。
点击Image names, 命令行窗口会提示你输入图片的basename以及图片的格式(比如你图片文件名是right1, right2, …, right10,basename就是right),然后Matlab会自动帮你读入这些图片,如下图所示,可以看到,读入了10幅右摄像头的棋盘图。
采集棋盘图的时候要注意,尽量让棋盘占据尽可能多的画面,这样可以得到更多有关摄像头畸变方面的信息
2.2. 图像basename读入
2.3. 读入的棋盘图
然后再回到主控制界面,点击Extract grid corners,提取每幅图的角点
2.4. calib_gui面板
点击完后,命令行会出现如下提示,主要是让你输入棋盘角点搜索窗口的大小。窗口定的大一点的话提取角点会比较方便点(即便点得偏离了也能找到),但也要注意不能大过一个方格的大小。剩下的两个选项,只要回车选用默认设置就可以了
2.5. 选择窗口大小
然后就开始了角点的提取工作,按一定顺序分别提取棋盘的最边上的角点,程序会自动帮你找到所有对应的角点
2.6. 提取角点
2.7. 提取角点2
在提取第一幅图的时候命令行窗口可能会提示你输入方格大小,这里输入你方格的实际大小就行,比如我方格是27mm,就输入27。这步事实上相当关键,它定义了空间的尺度,如果要对物体进行测量的话,这步是必须的。
按相同的方法提取完10幅图后,点击Calibration,开始摄像头标定
2.8. calib_gui面板
经过多次迭代后,程序会最终得到摄像头的内外参数,如下图所示(图中符号由于字体关系没有完全显示,中间的问号是表示误差的加减号)
2.9. Calibration迭代过程及结果
可以通过面板上的Show Extrinsic查看一下标定结果,可以验证一下标定外参数的结果
2.10. 外部参数图示
验证标定结果无误之后,就点击面板上的Save按钮,程序会把标定结果放在一个叫Calib_Result.mat中,为了方便后续立体标定,把这个文件名改为Calib_Result_right.mat。
左摄像头标定的方法与右摄像头相同,生成的Calib_Result.mat之后,将其改名为Calib_Result_left.mat就可以了
左右摄像头都标定完成之后,就可以开始立体标定了。
在Matlab命令行中键入stereo_gui启动立体标定面板,如下图所示
2.11. stereo_gui面板
点击Load left and right calibration files并在命令行中选择默认的文件名(Calib_Result_left.mat和Calib_Result_right.mat)之后就可以开始Run stereo calibration了,run之后的结果如下图所示,左右摄像头的参数都做了修正,并且也求出了两个摄像头之间的旋转和平移关系向量(om和T)
2.12. 立体标定结果
在面板上点击Show Extrinsics of stereo rig,可以看到如下图所示的双摄像头关系图,可以看到,两个摄像头基本是前向平行的
2.13. 双摄像头与定标棋盘间的位置关系
得到了立体标定参数之后,就可以把参数放入xml文件,然后用cvLoad读入OpenCV了。具体的方法可以参照Learning OpenCV第11章的例子,上面就是用cvSave保存标定结果,然后再用cvLoad把之前的标定结果读入矩阵的
2.14. xml文件示例
这里需要注意的是Matlab标定结果中的om向量,这个向量是旋转矩阵通过Rodrigues变换之后得出的结果,如果要在cvStereoRectify中使用的话,需要首先将这个向量用cvRodrigues转换成旋转矩阵。关于Rodrigues变换,Learning OpenCV的第11章也有说明。
2.15. 旋转矩阵的Rodrigues形式表示
3. 立体校准和匹配
有了标定参数,校准的过程就很简单了。
我使用的是OpenCV中的cvStereoRectify,得出校准参数之后用cvRemap来校准输入的左右图像。这部分的代码参考的是Learning OpenCV 十二章的例子。
校准之后,就可以立体匹配了。立体匹配OpenCV里面有两种方法,一种是Block Matching,一种是Graph Cut。Block Matching用的是SAD方法,速度比较快,但效果一般。Graph Cut可以参考Kolmogrov03的那篇博士论文,效果不错,但是运行速度实在是慢到不能忍。所以还是选择BM。
以下是我用BM进行立体匹配的参数设置
- BMState = cvCreateStereoBMState(CV_STEREO_BM_BASIC,0);
- assert(BMState != 0);
- BMState->preFilterSize=13;
- BMState->preFilterCap=13;
- BMState->SADWindowSize=19;
- BMState->minDisparity=0;
- BMState->numberOfDisparities=unitDisparity*16;
- BMState->textureThreshold=10;
- BMState->uniquenessRatio=20;
- BMState->speckleWindowSize=13;
其中minDisparity这个参数我设置为0是由于我的两个摄像头是前向平行放置,相同的物体在左图中一定比在右图中偏右,如下图3.1所示。所以没有必要设置回搜的参数。
如果为了追求更大的双目重合区域而将两个摄像头向内偏转的话,这个参数是需要考虑的。
3.1. 校正后的左右视图
另外需要提的参数是uniquenessRatio,实验下来,我感觉这个参数对于最后的匹配结果是有很大的影响。uniquenessRatio主要可以防止误匹配,其主要作用从下面三幅图的disparity效果比对就可以看出。在立体匹配中,我们宁愿区域无法匹配,也不要误匹配。如果有误匹配的话,碰到障碍检测这种应用,就会很麻烦。
3.2. UniquenessRatio为0时的匹配图,可以看到大片的误匹配区域
3.3. UniquenessRatio为10时的disparity map, 可以看到误匹配被大量减少了, 但还是有噪点
3.4. UniquenessRatio为20时的disparity map, 可以看到误匹配基本被去除了, 点云干净了很多
关于cvFindStereoCorrespondenceBM这个函数的源代码,曾经做过比较详细的研究,过一段时间也会把之前写的代码注释整理一下,发篇博文。
4. 实际距离的测量
在用cvFindStereoCorrespondenceBM得出disparity map之后,还需要通过cvReprojectImageTo3D这个函数将单通道Disparity Map转换成三通道的实际坐标矩阵。
具体的数学原理可以参考下面这个公式(from chenyusiyuan http://blog.csdn.net/chenyusiyuan/archive/2009/12/25/5072597.aspx,实际深度的一些问题这篇博文中也有提到)
4.1 距离转换公式
但是在实际操作过程中,用cvReprojectImageTo3D得到的数据并未如实际所想,生成深度矩阵所定义的世界坐标系我就一直没弄清楚。这在下面的例子中会详细说明,希望这方面的专家能帮忙解答一下:
图4.2是测量时的实际场景图,场景中主要测量的三个物体就是最前面的利乐包装盒、中间的纸杯、和最远的塑料瓶。
4.2. 实际场景中三个待测物体的位置
图4.3是校准后的左右图和匹配出来的disparity map,disparity窗口中是实际的点云,object窗口是给disparity map加了个阈值之后得到的二值图,主要是为了分割前景和背景。可以看到要测的三个物体基本被正确地分割出来了
4.3. 双目摄像头得到的disparity map
图4.4是在disparity窗口中选取一个点后然后在实际坐标矩阵中得到的对应三维信息,在这里,我在三个物体的点云上各选一个点来代表一个物体实际的坐标信息。(这里通过鼠标获取一点坐标信息的方法参考的是opencv sample里的watershed.cpp)
4.4. 对应点的三维坐标
在这里可以看到,(265, 156)也就是利乐包装盒的坐标是(13, 12, -157),(137, 142)纸杯的坐标是(77, 30, -312),(95, 115)塑料瓶的坐标是(144, 63, -482)。
补充一下:为了方便显示,所以视差图出来之后进行了一个0-255的normalize,所以value值的前一个是normalize之后点的灰度值,后一个是normalize之前点的实际视差图。
由cvFindStereoCorrespondenceBM算法的源代码:
目前我还是不是很清楚立体坐标系原点和尺度,但是从这三个点的z坐标可以大致看出这三个物体的距离差大概是1:2:3,基本与实际场景中物体的位置一致。因此,可以通过这种方法确定出物体的大致距离信息。
但是,如果就从摄像头参数本身来测量距离的话,就不是很明白了,还求这方面的大牛解答。
5. 一些问题
5.1 关于StereoCalibrate
OpenCV自带的cvStereoCalibrate感觉不怎么好用,用这个函数求出的内参外参和旋转平移矩阵进行校准,往往无法达到行对准,有时甚至会出现比较可怕的畸变。在看了piao的http://www.opencv.org.cn/forum/viewtopic.php?f=1&t=4603帖子之后,也曾经尝试过现用cvCalibrateCamera2单独标定(左右各20幅图),得出的结果基本和Matlab单独标定的相同,然后再在cvStereoCalibrate中将参数设成CV_CALIB_USE_INTRINSIC_GUESS,用来细化内参数和畸变参数,结果得出的标定结果就又走样了。
不知道有谁在这方面有过成功经验的,可以出来分享一下。毕竟用Matlab工具箱还是麻烦了些。
5.2 Translation向量以及立体匹配得出的世界坐标系
Learning OpenCV中对于Translation和Rotation的图示是这样的
5.1. Learning OpenCV中的图示
可是在实验过程中发现,如果将Translation向量按尺度缩放,对于StereoRectify之后的左右视图不会有变化,比如将T = [ -226.73817 -0.62302 8.93984 ] ,变成T = [ -22.673817 -0.062302 0.893984 ],在OpenCV中显示的结果不会有任何变化。而且我如果修改其中的一个参量的话,左右视图发生的变化也不是图5.1中所示的那种变化(比如把x缩小,那么视图发生的变化不是往x轴方向的平移)。
因此又回到了老问题,这里这些坐标的尺度究竟是什么?通过ReprojectTo3D那个函数得到的三维坐标又是以哪个点为原点,那三个方向为x,y,z轴的?
补充: 对这个问题的解答来自于和maxwellsdemon的讨论
他的解释如下:rotation是两者的旋转角度的关系,但是你要把它矫正平行,也是需要translation matrix的。你可以设想,两个看似已经平行了的摄像头,但是深度上放置的有差距,那么在矫正的时候会议translation matrix所对应的角度或者直线为基准,二者旋转一个小角度,使得完全平行。