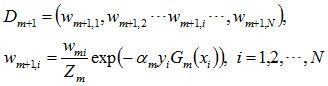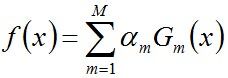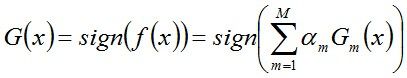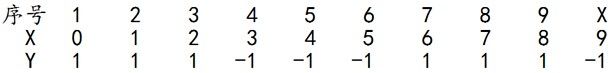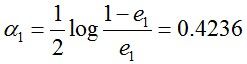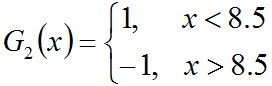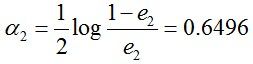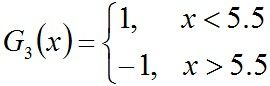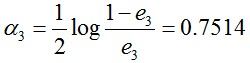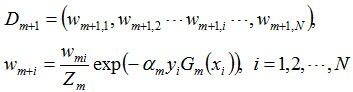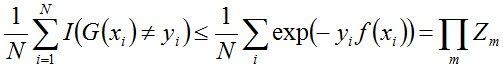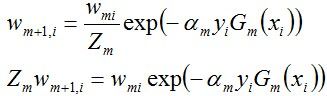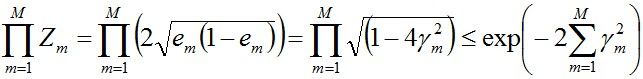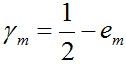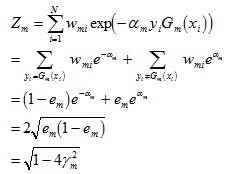Adaboost 算法实例解析

 Adaboost 算法实例解析

1 Adaboost的原理

1.1 Adaboost基本介绍   

    AdaBoost，是英文"Adaptive Boosting"（自适应增强）的缩写，由Yoav Freund和Robert Schapire在1995年提出。Adaboost是一种迭代算法，其核心思想是针对同一个训练集训练不同的分类器(弱分类器)，然后把这 Adaboost 些弱分类器集合起来，构成一个更强的最终分类器(强分类器)。其算法本身是通过改变数据分布来实现的，它根据每次训练集之中每个样本的分类是否正确，以及上次的总体分类的准确率，来确定每个样本的权值。将修改过权值的新数据集送给下层分类器进行训练，最后将每次训练得到的分类器最后融合起来，作为最后的决策分类器。使用adaboost分类器可以排除一些不必要的训练数据特徵，并将关键放在关键的训练数据上面。

主要解决的问题
　　目前，对adaBoost算法的研究以及应用大多集中于分类问题，同时近年也出现了一些在回归问题上的应用。就其应用adaBoost系列主要解决了: 两类问题、多类单标签问题、多类多标签问题、大类单标签问题，回归问题。它用全部的训练样本进行学习。

1.2 Adaboost算法介绍

算法分析　

　该算法其实是一个简单的弱分类算法提升过程，这个过程通过不断的训练，可以提高对数据的分类能   Adaboost
力。整个过程如下所示： 　　

       1. 先通过对N个训练样本的学习得到第一个弱分类器； 　　

       2. 将分错的样本和其他的新数据一起构成一个新的N个的训练样本，通过对这个样本的学习得到第二个弱分类器 ； 　　
       3. 将1和2都分错了的样本加上其他的新样本构成另一个新的N个的训练样本，通过对这个样本的学习得到第三个弱分类器；

　　4. 最终经过提升的强分类器 。即某个数据被分为哪一类要通过 ， ……的多数表决。

    Adaboost的自适应在于：前一个基本分类器分错的样本会得到加强，加权后的全体样本再次被用来训练下一个基本分类器。同时，在每一轮中加入一个新的弱分类器，直到达到某个预定的足够小的错误率或达到预先指定的最大迭代次数。

     具体说来，整个Adaboost 迭代算法就3步：

1. 初始化训练数据的权值分布。如果有N个样本，则每一个训练样本最开始时都被赋予相同的权重：1/N。
   
2. 训练弱分类器。具体训练过程中，如果某个样本点已经被准确地分类，那么在构造下一个训练集中，它的权重就被降低；相反，如果某个样本点没有被准确地分类，那么它的权重就得到提高。然后，权重更新过的样本集被用于训练下一个分类器，整个训练过程如此迭代地进行下去。
3. 将各个训练得到的弱分类器组合成强分类器。各个弱分类器的训练过程结束后，加大分类误差率小的弱分类器的权重，使其在最终的分类函数中起着较大的决定作用，而降低分类误差率大的弱分类器的权重，使其在最终的分类函数中起着较小的决定作用。换言之，误差率低的弱分类器在最终分类器中占的权重较大，否则较小。

 Adaboost算法流程

    给定一个训练数据集T={(x1,y1), (x2,y2)…(xN,yN)}，其中实例，而实例空间，yi属于标记集合{-1,+1}，Adaboost的目的就是从训练数据中学习一系列弱分类器或基本分类器，然后将这些弱分类器组合成一个强分类器。

    Adaboost的算法流程如下：

• 步骤1. 首先，初始化训练数据的权值分布。每一个训练样本最开始时都被赋予相同的权重：1/N。

• 步骤2. 进行多轮迭代，用m = 1,2, ..., M表示迭代的第多少轮

a. 使用具有权值分布Dm的训练数据集学习，得到基本分类器：

b. 计算Gm(x)在训练数据集上的分类误差率

由上述式子可知，Gm(x)在训练数据集上的误差率em就是被Gm(x)误分类样本的权值之和。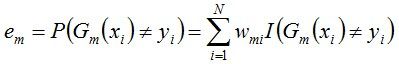

c. 计算Gm(x)的系数，am表示Gm(x)在最终分类器中的重要程度（目的：得到基本分类器在最终分类器中所占的权重）：

由上述式子可知，em <= 1/2时，am >= 0，且am随着em的减小而增大，意味着分类误差率越小的基本分类器在最终分类器中的作用越大。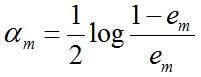

d. 更新训练数据集的权值分布（目的：得到样本的新的权值分布），用于下一轮迭代

使得被基本分类器Gm(x)误分类样本的权值增大，而被正确分类样本的权值减小。就这样，通过这样的方式，AdaBoost方法能“聚焦于”那些较难分的样本上。

    其中，Zm是规范化因子，使得Dm+1成为一个概率分布：

• 步骤3. 组合各个弱分类器

从而得到最终分类器，如下：

对于这个算法需要介绍的是：

1.         算法开始前，需要将每个样本的权重初始化为1/m,这样一开始每个样本都是等概率的分布，每个分类器都会公正对待。

2.         开始迭代后，需要计算每个弱分类器的分类错误的误差，误差等于各个分错样本的权重和，这里就体现了样本权重的作用。如果一个分类器正确分类了一个权重大的样本，那么这个分类器的误差就会小，否则就会大。这样就对分类错误的样本更大的关注。

3.         获取最优分类器后，需要计算这个分类器的权重，然后再更新各个样本的权重，然后再归一化

4.         算法迭代的次数一般不超过弱分类器的个数，如果弱分类器的个数非常之多，那么可以权衡自己性价比来折中选择。

5.         迭代完成后，最后的分类器是由迭代过程中选择的弱分类器线性加权得到的。

1.3 Adaboost实例解析

   例1. 下面，给定下列训练样本，请用AdaBoost算法学习一个强分类器。

    

    求解过程：初始化训练数据的权值分布，令每个权值W1i = 1/N = 0.1，其中，N = 10，i = 1,2, ..., 10，然后分别对于m = 1,2,3, ...等值进行迭代。

    拿到这10个数据的训练样本后，根据 X 和 Y 的对应关系，要把这10个数据分为两类，一类是“1”，一类是“-1”，根据数据的特点发现：“0 1 2”这3个数据对应的类是“1”，“3 4 5”这3个数据对应的类是“-1”，“6 7 8”这3个数据对应的类是“1”，9是比较孤独的，对应类“-1”。抛开孤独的9不讲，“0 1 2”、“3 4 5”、“6 7 8”这是3类不同的数据，分别对应的类是1、-1、1，直观上推测可知，可以找到对应的数据分界点，比如2.5、5.5、8.5 将那几类数据分成两类。当然，这只是主观臆测，下面实际计算下这个过程。

迭代过程1

对于m=1，在权值分布为D1（10个数据，每个数据的权值皆初始化为0.1）的训练数据上，经过计算可得：

1. 阈值v取2.5时误差率为0.3（x < 2.5时取1，x > 2.5时取-1，则6 7 8分错，误差率为0.3），
2. 阈值v取5.5时误差率最低为0.4（x < 5.5时取1，x > 5.5时取-1，则3 4 5 6 7 8皆分错，误差率0.6大于0.5，不可取。故令x > 5.5时取1，x < 5.5时取-1，则0 1 2 9分错，误差率为0.4），
3. 阈值v取8.5时误差率为0.3（x < 8.5时取1，x > 8.5时取-1，则3 4 5分错，误差率为0.3）。

所以无论阈值v取2.5，还是8.5，总得分错3个样本，故可任取其中任意一个如2.5，弄成第一个基本分类器为：

上面说阈值v取2.5时则6 7 8分错，所以误差率为0.3，更加详细的解释是：因为样本集中

1. 0 1 2对应的类（Y）是1，因它们本身都小于2.5，所以被G1(x)分在了相应的类“1”中，分对了。
2. 3 4 5本身对应的类（Y）是-1，因它们本身都大于2.5，所以被G1(x)分在了相应的类“-1”中，分对了。
3. 但6 7 8本身对应类（Y）是1，却因它们本身大于2.5而被G1(x)分在了类"-1"中，所以这3个样本被分错了。
4. 9本身对应的类（Y）是-1，因它本身大于2.5，所以被G1(x)分在了相应的类“-1”中，分对了。
   

从而得到G1(x)在训练数据集上的误差率（被G1(x)误分类样本“6 7 8”的权值之和）e1=P(G1(xi)≠yi) = 3*0.1 = 0.3。

然后根据误差率e1计算G1的系数：

这个a1代表G1(x)在最终的分类函数中所占的权重，为0.4236。
接着更新训练数据的权值分布，用于下一轮迭代：

值得一提的是，由权值更新的公式可知，每个样本的新权值是变大还是变小，取决于它是被分错还是被分正确。

即如果某个样本被分错了，则yi * Gm(xi)为负，负负等正，结果使得整个式子变大（样本权值变大），否则变小。

第一轮迭代后，最后得到各个数据新的权值分布D2 = (0.0715, 0.0715, 0.0715, 0.0715, 0.0715,  0.0715, 0.1666, 0.1666, 0.1666, 0.0715)。由此可以看出，因为样本中是数据“6 7 8”被G1(x)分错了，所以它们的权值由之前的0.1增大到0.1666，反之，其它数据皆被分正确，所以它们的权值皆由之前的0.1减小到0.0715。

分类函数f1(x)= a1*G1(x) = 0.4236G1(x)。

此时，得到的第一个基本分类器sign(f1(x))在训练数据集上有3个误分类点（即6 7 8）。

    从上述第一轮的整个迭代过程可以看出：被误分类样本的权值之和影响误差率，误差率影响基本分类器在最终分类器中所占的权重。

 迭代过程2

对于m=2，在权值分布为D2 = (0.0715, 0.0715, 0.0715, 0.0715, 0.0715,  0.0715, 0.1666, 0.1666, 0.1666, 0.0715)的训练数据上，经过计算可得：

1. 阈值v取2.5时误差率为0.1666*3（x < 2.5时取1，x > 2.5时取-1，则6 7 8分错，误差率为0.1666*3），
2. 阈值v取5.5时误差率最低为0.0715*4（x > 5.5时取1，x < 5.5时取-1，则0 1 2 9分错，误差率为0.0715*3 + 0.0715），
3. 阈值v取8.5时误差率为0.0715*3（x < 8.5时取1，x > 8.5时取-1，则3 4 5分错，误差率为0.0715*3）。

所以，阈值v取8.5时误差率最低，故第二个基本分类器为：

面对的还是下述样本：

很明显，G2(x)把样本“3 4 5”分错了，根据D2可知它们的权值为0.0715, 0.0715,  0.0715，所以G2(x)在训练数据集上的误差率e2=P(G2(xi)≠yi) = 0.0715 * 3 = 0.2143。

计算G2的系数：

更新训练数据的权值分布：

D3 = (0.0455, 0.0455, 0.0455, 0.1667, 0.1667,  0.01667, 0.1060, 0.1060, 0.1060, 0.0455)。被分错的样本“3 4 5”的权值变大，其它被分对的样本的权值变小。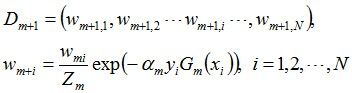
f2(x)=0.4236G1(x) + 0.6496G2(x)

此时，得到的第二个基本分类器sign(f2(x))在训练数据集上有3个误分类点（即3 4 5）。

 迭代过程3

对于m=3，在权值分布为D3 = (0.0455, 0.0455, 0.0455, 0.1667, 0.1667,  0.01667, 0.1060, 0.1060, 0.1060, 0.0455)的训练数据上，经过计算可得：

1. 阈值v取2.5时误差率为0.1060*3（x < 2.5时取1，x > 2.5时取-1，则6 7 8分错，误差率为0.1060*3），
2. 阈值v取5.5时误差率最低为0.0455*4（x > 5.5时取1，x < 5.5时取-1，则0 1 2 9分错，误差率为0.0455*3 + 0.0715），
3. 阈值v取8.5时误差率为0.1667*3（x < 8.5时取1，x > 8.5时取-1，则3 4 5分错，误差率为0.1667*3）。

所以阈值v取5.5时误差率最低，故第三个基本分类器为（下图画反了，待后续修正）：

依然还是原样本：

此时，被误分类的样本是：0 1 2 9，这4个样本所对应的权值皆为0.0455，

所以G3(x)在训练数据集上的误差率e3= P(G3(xi)≠yi) = 0.0455*4 = 0.1820。

计算G3的系数：

更新训练数据的权值分布：

D4 = (0.125, 0.125, 0.125, 0.102, 0.102,  0.102, 0.065, 0.065, 0.065, 0.125)。被分错的样本“0 1 2 9”的权值变大，其它被分对的样本的权值变小。

f3(x)=0.4236G1(x) + 0.6496G2(x)+0.7514G3(x)

此时，得到的第三个基本分类器sign(f3(x))在训练数据集上有0个误分类点。至此，整个训练过程结束。

    G(x) = sign[f3(x)] = sign[ a1 * G1(x) + a2 * G2(x) + a3 * G3(x) ]，将上面计算得到的a1、a2、a3各值代入G(x)中，得到最终的分类器为：G(x) = sign[f3(x)] = sign[ 0.4236G1(x) + 0.6496G2(x)+0.7514G3(x) ]。

图文解释可以参考：http://blog.csdn.net/haidao2009/article/details/7514787

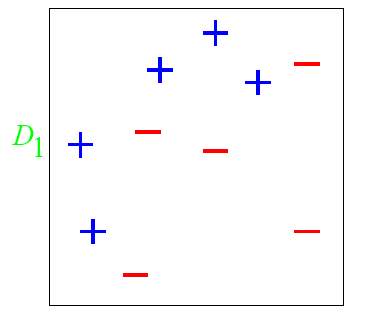
下面用图示说明adaboost的实现过程：

　　图中，“+”和“-”分别表示两种类别，在这个过程中，我们使用水平或者垂直的直线作为分类器，来进行分类。

　　第一步：

　　根据分类的正确率，得到一个新的样本分布D_2­，一个子分类器h₁

　　其中划圈的样本表示被分错的。在右边的途中，比较大的“+”表示对该样本做了加权。

也许你对上面的ɛ1，ɑ1怎么算的也不是很理解。下面我们算一下，不要嫌我啰嗦，我最开始就是这样思考的，只有自己把算法演算一遍，你才会真正的懂这个算法的核心，后面我会再次提到这个。

算法最开始给了一个均匀分布 D 。所以h1 里的每个点的值是0.1。ok，当划分后，有三个点划分错了，根据算法误差表达式得到 误差为分错了的三个点的值之和，所以ɛ1=(0.1+0.1+0.1)=0.3，而ɑ1 根据表达式 的可以算出来为0.42. 然后就根据算法 把分错的点权值变大。如此迭代，最终完成adaboost算法。

　　第二步：

　　根据分类的正确率，得到一个新的样本分布D₃，一个子分类器h₂

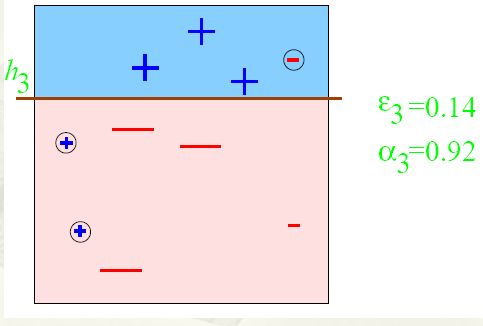
　　第三步：

　　得到一个子分类器h₃

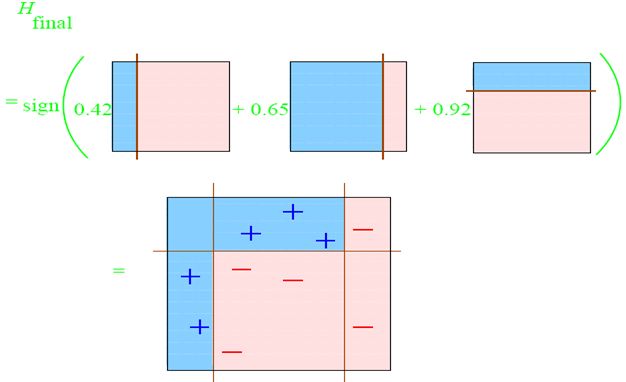
　　整合所有子分类器：

　　因此可以得到整合的结果，从结果中看，及时简单的分类器，组合起来也能获得很好的分类效果，在例子中所有的。

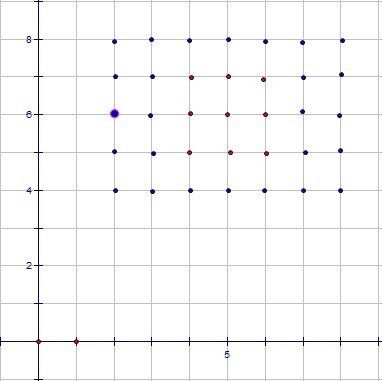
例2. 如下图在二维平面上分布了如下两种颜色的点，不同颜色的点代表了不同类别的数据，一般来讲用线性分类器是不可分的，因为没有明显的分界线，但是现在需要用adaboost算法将他们分开。

                                                     

 

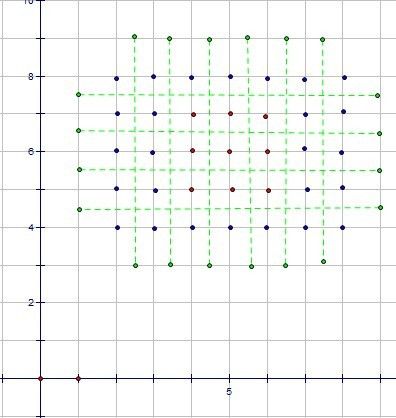
         用adaboost算法进行分类，那么首先需要定义的就是弱分类器，如下图，我们可以定义如下图虚线所示的弱分类器。

 

        初始化各个样本的权重后就可以开始迭代了，依照wiki上的算法框架下面给出了算法进行20次迭代后，选择的分类器的情况如下：

iteration 0 [ (-inf, 8.5) y ] -0.530435980343

iteration 1 [ (6.5, inf) x ] -0.405465108108

iteration 2 [ (-inf, 3.5) x ] -0.362281688397

iteration 3 [ (-inf, 8.5) y ] -0.50229166951

iteration 4 [ (7.5, inf) y ] -0.329115179032

iteration 5 [ (8.5, inf) y ] 0.245959304836

iteration 6 [ (4.5, inf) y ] 0.394479043549

iteration 7 [ (-inf, 8.5) y ] -0.279930813609

iteration 8 [ (3.5, inf) x ] 0.392890051159

iteration 9 [ (-inf, 6.5) x ] 0.282848009329

iteration 10 [ (8.5, inf) y ] 0.45910361684

iteration 11 [ (-inf, 7.5) y ] 0.316216082219

iteration 12 [ (-inf, 8.5) y ] -0.238788369567

iteration 13 [ (6.5, inf) x ] -0.342006845132

iteration 14 [ (8.5, inf) y ] 0.25296754864

iteration 15 [ (-inf, 4.5) y ] -0.36650324231

iteration 16 [ (-inf, 8.5) y ] -0.265860506761

iteration 17 [ (-inf, 3.5) x ] -0.416892893363

iteration 18 [ (-inf, 8.5) y ] -0.290721983964

iteration 19 [ (7.5, inf) y ] -0.322597760403

         将这二十个弱分类器线性组合起来得到的分类完全正确。当然这个完全正确是因为构造的数据的原因。但是从这个例子可以看出adaboost确实是一个非常不错的分类算法。

代码实现：https://github.com/zengkui/machine-learning/blob/master/Adaboost/adaboost.py

此代码就是针对上例给出的可执行的python代码

2 Adaboost的误差界

  通过上面的例子可知，Adaboost在学习的过程中不断减少训练误差e，直到各个弱分类器组合成最终分类器，那这个最终分类器的误差界到底是多少呢？

事实上，Adaboost 最终分类器的训练误差的上界为：

下面，咱们来通过推导来证明下上述式子。

当G(xi)≠yi时，yi*f(xi)<0，因而exp(-yi*f(xi))≥1，因此前半部分得证。

关于后半部分，别忘了：

整个的推导过程如下：

    这个结果说明，可以在每一轮选取适当的Gm使得Zm最小，从而使训练误差下降最快。接着，咱们来继续求上述结果的上界。

    对于二分类而言，有如下结果：

    其中，。

    继续证明下这个结论。

    由之前Zm的定义式跟本节最开始得到的结论可知：

    而这个不等式可先由e^x和1-x的开根号，在点x的泰勒展开式推出。

    值得一提的是，如果取γ1, γ2… 的最小值，记做γ（显然，γ≥γi>0，i=1,2,...m），则对于所有m，有：

    这个结论表明，AdaBoost的训练误差是以指数速率下降的。另外，AdaBoost算法不需要事先知道下界γ，AdaBoost具有自适应性，它能适应弱分类器各自的训练误差率 。

    最后，Adaboost 还有另外一种理解，即可以认为其模型是加法模型、损失函数为指数函数、学习算法为前向分步算法的二类分类学习方法，有机会再推导下，然后更新此文。而在此之前，有兴趣的可以参看《统计学习方法》第8.3节或其它相关资料。

3 模型的优缺点

毫无疑问这个模型的最大的一个优点是可以自动的组合弱分类器，这在实际应用中的便利之处十分明显。 人类大脑很擅长于总结各种规律，从而制定规则来进行数据处理，但是当规则变多后，怎么组织这些规则在一起共同发挥作用，这时候人的大脑的局限性就非常明显了，而adaboost算法正好弥补了这一点。此外算法本身简单，高效，易于编写而且训练过程是没有参数需要调节的。

但是adaboost也是有确点的，并不是所有问题都能搞定，从wiki上介绍的来看，adaboost对于噪音数据和异常数据是十分敏感的。

4 补充：boosting与AdaBoost

对于boosting算法，存在两个问题： 　
　
       1. 如何调整训练集，使得在训练集上训练的弱分类器得以进行； 　　

       2. 如何将训练得到的各个弱分类器联合起来形成强分类器。
　　
       针对以上两个问题，adaBoost算法进行了调整： 　
　
       1. 使用加权后选取的训练数据代替随机选取的训练样本，这样将训练的焦点集中在比较难分的训练数
据样本上； 　　

      2. 将弱分类器联合起来，使用加权的投票机制代替平均投票机制。让分类效果好的弱分类器具有较大的权重，而分类效果差的分类器具有较小的权重。　　

       AdaBoost算法是Freund和Schapire根据在线分配算法提出的，他们详细分析了AdaBoost算法错误率的上界，以及为了使强分类器达到错误率，算法所需要的最多迭代次数等相关问题。与Boosting算法不同的是，adaBoost算法不需要预先知道弱学习算法学习正确率的下限即弱分类器的误差，并且最后得到的强分类器的分类精度依赖于所有弱分类器的分类精度，这样可以深入挖掘弱分类器算法的能力。　

       AdaBoost算法中不同的训练集是通过调整每个样本对应的权重来实现的。开始时，每个样本对应的权重是相同的，即其中 n 为样本个数，在此样本分布下训练出一弱分类器。对于分类错误的样本，加大其对应的权重；而对于分类正确的样本，降低其权重，这样分错的样本就被突出出来，从而得到一个新的样本分布。在新的样本分布下，再次对弱分类器进行训练，得到弱分类器。依次类推，经过 T 次循环，得到 T 个弱分类器，把这 T 个弱分类器按一定的权重叠加（boost）起来，得到最终想要的强分类器。 

5 参考文献与推荐阅读

1. wikipedia上关于Adaboost的介绍：http://zh.wikipedia.org/zh-cn/AdaBoost；
2. 邹博之决策树与Adaboost PPT：http://pan.baidu.com/s/1hqePkdY；
3. 《统计学习方法 李航著》第8章；
4. 关于adaboost的一些浅见：http://blog.sina.com.cn/s/blog_6ae183910101chcg.html；
5. A Short Introduction to Boosting：http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.93.5148&rep=rep1&type=pdf；
   
6. 南大周志华教授做的关于boosting 25年的报告PPT：http://vdisk.weibo.com/s/FcILTUAi9m111；
7. 《数据挖掘十大算法》第7章 Adaboost；
8. http://summerbell.iteye.com/blog/532376；
   
9. 统计学习那些事：http://cos.name/2011/12/stories-about-statistical-learning/；
10. 统计学习基础学习笔记：http://www.loyhome.com/%E2%89%AA%E7%BB%9F%E8%AE%A1%E5%AD%A6%E4%B9%A0%E7%B2%BE%E8%A6%81the-elements-of-statistical-learning%E2%89%AB%E8%AF%BE%E5%A0%82%E7%AC%94%E8%AE%B0%EF%BC%88%E5%8D%81%E5%9B%9B%EF%BC%89/；