开源分词框架分析
本文将带你一起了解搜索引擎神秘面纱中的一个重要部分---中文分词技术:主要讲述中文分词的实现原理和现今比较热门的几种搜索分词java版开源框架。
任何一个全文搜索引擎都必须要在对索引处理之前进行一项重要的数据预处理工作:分词。分词的作用在于让机器能够更加容易的"学会"人类语言,搜索引擎才能展示出我们真正想要找的东西。当然,如果仅仅只是针对搜索这个应用场景,对外文(英文,俄文)的分词工作似乎轻而易举,因为一段e文中每一个有意义的词语都是以空格或者符号隔开的,我们只需要根据空格就可以完成最基本的分词工作。但是中文(其实还有日文,韩文,或许你会想到CJK)就没有这么简单了,正如我现在写的一般,词间是没有空格的,加上中国汉字"博大精深",一般的办法是解决不了中文分词的。
假如现在要你设计一个算法,实现中文分词,"二分法"似乎是最容易想到,却也是最不给力的一种算法,虽然简单,但是结果精确性却不高(大概的思路就是把"淘宝被拆了"分成"淘宝","宝被","被拆","拆了",然后将这些词到词库里去筛选)。这种分词思想的优点在于简单容易实现,缺点是词库量大,而且二义性问题似乎是个老大难。比如"淘宝贝"最后被分成了"淘宝"和"贝",但是正确的切分应该是"淘"和"宝贝";它和单字法一样,都需要基于"辞典"这个数据结构来完成分词工作。基于辞典的中文分词算法是北航教授梁南元最早提出来的,这种算法的思想后来衍生成了很多种算法:比如最少词数分词技术,即一句话应该分隔成词数最少个数的词语串,也就是我们经常提及的正向最大匹配算法fmm:这个算法的流程图如下所示:
当然,以上实现只是最简单的实现,因为L的大小是固定的,所以其精确性和二义性还存在很大的问题;我们还可以在此基础之上对算法进行改造处理,有兴趣的同学可以网上搜索相关的优化算法;
除此之外,还有反向最大匹配算法RMMS,它和正向最大匹配算法的唯一的区别在于它是从一个句子的结尾处开始扫描的;但是这两种算法都有一个比较严重的问题:就是在遇到二义性的情况下,分词结果可能不是十分精确(实践证明,逆向最大匹配分词出来的结果往往二义性的错误比正向匹配的少很多,但是依旧存在),所以为了减少因为岐义造成的不准确性,有些人就尝试使用两次扫描:即正向最大匹配和逆向最大匹配各一次,两次匹配出来的结果再做二次处理分析,我们称为双向匹配,并且收到了很好的效果,提高了分词的准确率,但是性能很明显要下降很多。顺便说一下,有相关SEO人员研究谷歌和百度的中文分词都采用的是正向最大匹配算法来实现分词的,只是百度在辞典上做了更多的文章(把辞典分为专业辞典和普通辞典),所以在分词上比谷歌做的稍微好一些,因为无法得到证实,所以只能姑且这般相信了。
说完了算法流程,再来介绍一个实现最大匹配算法的数据结构-Tire树:
如下两图显示,其实它就是一棵字典树,它用于存储大量的字符串以便支持快速模式匹配,所以是实现最大匹配算法的不二选择。它的特点是所有含有公共前缀的字符串将挂在书中同一个节点下,且每个字符串不能称为另外一个字符串的前缀(可用通过添加特殊字符到字符串末尾的方式解决这个问题),它的查询时间复杂度为O(n×d),n为树的高度,d为辞典的大小。
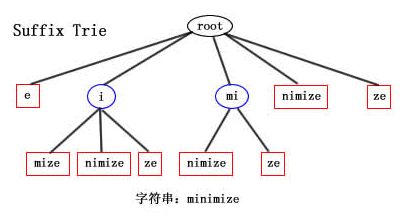
以上是最标准的Tire树的结构,其实Tire树还有压缩tire和后缀式tire.先来看看suffix Tire树:
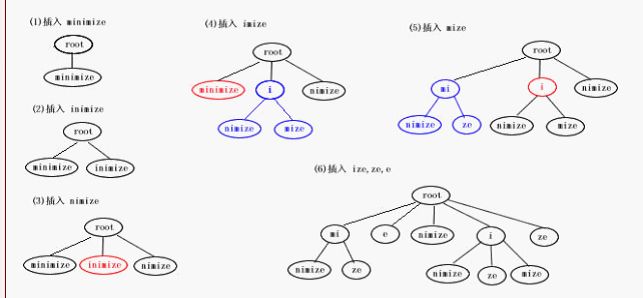
suffix Tire树是由指定字符串的后缀子串构成的一棵树;假如要构建"minimize"的suffix tire tree的话,首先它的后缀集合是{minimize,inimize,nimize,imize,mize,ize,ze,e},minimize suffix tire tree的构建过程是这样的:
构建后缀式tire树的一个原则是:当插入新的字串时,如果新字串和已有叶子节点的字串有共同的前缀,需要将已有叶子节点拆分成两个叶子节点。
按照后缀式tire tree查找P子串的算法是:
从root根节点开始遍历其所有的孩子节点;
如果没有一个孩子节点的第一个字符和P的第一个字符相等,匹配失败,结束;
如果节点N的关键字第一个字符与p第一个字符相等;
a. N.length>=P.length;如果N.sub(0,P.len-1)=P,匹配成功;
b. N.length<=P.length;如果P.sub(0,N.len-1)=N,那么p1=p.subString(N.length);root=N continue 1;
如果使用hash直接定位的话,该查找算法的时间复杂度O(P.length),查询效率可见一斑;
压缩Tire树:
压缩Trie类似于标准Trie,一样可以快速查找前缀串,但它能保证trie中的每个内部结点至少有两个子节点(根结点除外),通过把单子结点链压缩进叶子节点来执行这个规则。如果T的一个非根内部结点v只有一个子结点,那么我们称v是冗余的,相连的两个冗余节点会构成一个冗余链,这个时候我们就可以用单边来代替冗余节点,如下图所示:
这种压缩表示的一个巨大的优点就是:无论结点需要存储多长的字串,全部都可以用一个三元组表示,而且三元组所占的空间是固定有限的。如下图所示:
上面我们提到了正向最大匹配算法,逆向最大匹配算法,双向最大匹配算法的原理,算法流程,优劣和算法的性能,好的数据结构实现etc。但是不得不说明,解决二义性分词问题的成功解决方案是对语料库进行语言建模---使用统计语言模型来处理分词,它的准确性比基于辞典的分词算法整整提高了一个数量级,网上有相关资料介绍谷歌如何基于统计的思想来建模生成它的词库。
说到统计,大概不得不提一下伟大的数学家香浓,正是他的朴素贝叶斯算法理论给我们的分词技术提供了很好的理论基础。谷歌的很多应用也是基于这个模型进行设计的,比如我们常用的"谷歌翻译"。这个统计语言模型大概是这样的:
假若一句话可以被拆分成N中分词方式:
(1)分词方式1:A1,A2,A3,......Aj;
(2)分词方式2:B1,B2,B3,......Bj;
......
(n)分词方式N:N1,N2,N3,......Nj;这N种分词方式中出现概率最大的分词方式,准确率就高。我们用数学方式来表达就是:P(Y|X) ∝ P(Y)*P(X|Y) ,基于统计的分词中:X 为字串(句子),Y 为词串(一种特定的分词假设) ,我们就是需要寻找使得 P(Y|X) 最大的 Y
联合概率的公式展开:
P(Y) = P(W1, W2, W3, ..) = P(W1) * P(W2|W1) * P(W3|W2, W1) * P(....)
我们假设句子中一个词的出现概率只依赖于它前面的有限的 k 个词 ,如果只依赖于前面的一个词,就是2元语言模型(2-gram),同理有 3-gram etc。当然,穷举所有的分词方式并计算其概率,其计算量也是很大的。这个时候就需要借助一些比较实用和高效的算法,比如"动态规划"算法来完善。
当然,如果你希望你的分词结果更加精确,你还可以在基于统计概率的基础上再做优化:对分词出来的结果进行查询,根据查询结果反馈是否这样的分词是合理/常见的。
回到我们说的搜索引擎之分词技术这个主题,要说明一点的是,分词的过程不仅仅是切割的过程,还有很多其他的工作。
预处理:在预处理阶段我们还要对句子进行编码转换 ,删除空格 ,标准化 ,数字识别 ,英文识别, 人名识别,地名识别等等一系列转换操作,包括百度,淘宝等在内的一些搜索引擎必不可少的需要经过这一步处理,这样处理出来的结果才能更好的进行分词工作。
后处理:在分词之后,我们还需要进行 单字合成 ,后缀处理 ,两字处理复合词 ,短语纠错 , 多输出 词性标注,恢复空格 ,编码转换等等工作。
以上主要介绍一些理论性的知识,下面我们来看看一些实际例子吧。其实在java开源社区,因为lucene搜索工具包的不断更新,性能越来越高,对lucene和Solr的企业级应用也越来越多,随之产生的java版分词工具包也如雨后春笋般冒出来。大家比较有印象的应该是IK和Paoding中文分词器,IK在iteye上介绍很多,对于lucene的常用用户,paoding获取你是最熟悉不过的了。
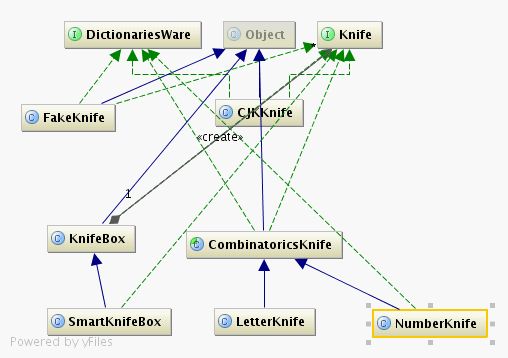
我们先来看看paoding分词。性能:在PIII 1G内存个人机器上,1秒可准确分词100万汉字。它主要采用基于"不限制个数"的词典文件对文章进行有效切分。看一下paoding的代码:它有一个Beef类即为"牛",然后可以用很多的Knife去切,谓之"庖丁解牛":
然后在使用的时候只要配置文件中指定好使用哪种knife来进行切割分词就好了。当然你也可以使用多个knife来进行切割,我们的knifeBox和SmartKnifeBox类就是支持多个knife切割的,box承担的主要工作则是对遇到的某个词进行决策,到底使用哪种具体的knife来进行切割。我们以CJKKnife为例:它的算法实现是正向最大匹配算法:从字符串的开始查找辞典中是否存在最大匹配的值;
paoding中定义了一堆的dictionary用于查找,其中有一个DictionaryDelegate类提供我们扩展实现自己的Dictionary;
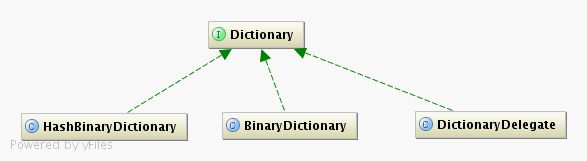
我们先来看一下HashBinaryDictionary这个类:
private Word[] ascWords;这个属性说明所有的词都是被加载到内存中的,
/**
* 首字符到分词典的映射
*/
private Map/* <Object, SubDictionaryWrap> */subs;这个属性保存的是首字符到分词典的映射关系,也就是说当字典长度很小的时候可以直接用一个BinaryDictionary来保存字典的值,但是如果辞典的量很大的时候,就有必要将一个词典以首字符拆分成多个词典,这样每次查找的时候可以先马上hash到分词典,然后在集合较小的分辞典上再查询,这样就极大的提高了分词查找的效率。
如果找到了需要切割的词,它会调用 Collector类中的collect方法保存分词的结果:

除此之外,paoding还支持添加过滤词典:如果待分析词在过滤列表中,那将不会被分词。
paoding分词器现在使用非常广泛,包括淘宝的终搜java搜索服务端应用也是采用了paoding分词框架。而IKAnalyzer则是一个以开源项目Luence为应用主体的,结合词典分词和文法分析算法的中文分词组件。它使用了"正向迭代最细粒度切分算法",支持细粒度和最大词长两种切分模式;具有83万字/秒(1600KB/S)的高速处理能力,采用了多子处理器分析模式,支持:英文字母、数字、中文词汇等分词处理,兼容韩文、日文字符优化的词典存储,更小的内存占用。支持用户词典扩展定。它的IKQueryParser实现了对分词歧义结果的非冲突排列组合,对lucene3.0的查询做了很好的支持和升级工作,推荐可以尝试用用,至于具体实现这里不再多说,请参看相关资料。
当然,除此之外,还有一个java的中文分词框架不得不提:MMSeg4j,它是MMSeg的java实现,支持中文分词。而MMSeg 算法有两种分词方法:Simple和Complex,原始版本是c实现的,都是基于正向最大匹配算法实现的。Complex 加了四个规则过虑。官方给出的正确识别率达到了 98.41%,mmseg4j 已经实现了这两种分词算法。1.5~1.6版本内存消耗在10M左右,simple算法的分词速度是1.1M/s,complex算法的分词速度是700kb/s。而1.7版本内存占用50M,complex速度1.2M/s,simple速度1.9M/s。毋庸置疑,MMseg4J也很好的支持Lucene和Solr。当然它也有对应的C++版本:LibMMSeg,,在基于SphinxSearch开发的coreseek开源搜索引擎也是使用了 LibMMSeg进行中分分词。不过其实sphinxsearch本身就已经支持mmseg分词算法。接下来我们看看mmseg的算法实现吧。
前面已经说过,mmseg算法也是基于正向最大匹配来完成的,但是它能有很高的准确性的原因是因为它在此基础上,添加了4条规则。这些规则中涉及一个概念:chunk,一个chunk就是对于句子的一种分词可能(一种候选分词结果),对于句子,每个chunk定义以下几个属性,长度(Length)、平均长度(Average Length)、标准差的平方(Variance)和自由语素度(Degree Of Morphemic Freedom):
属性 含义
长度(Length) chuck中各个词的长度之和
平均长度(Average Length) 长度(Length)/词数
标准差的平方(Variance) 同数学中的定义
自由语素度(Degree Of Morphemic Freedom) 各单字词词频的对数之和
主要的规则如下:
规则1:取最大匹配的chunks (Rule 1: Maximum matching) ,即取chunk长度最长的几个。
规则2:取平均词长最大的chunks(Rule 2: Largest average word length) ,即取chunk平均长度最长的几个。
规则3:取词长标准差最小的chunks (Rule 3: Smallest variance of word lengths) ,取词长标准差最小的几个。
规则4:取单字词自由语素度之和最大的chunk (Rule 4: Largest sum of degree of morphemic freedom of one-character words),这里要利用一个单字的词频词典,比如说"的"字的出现频率很高,那么我们倾向于认为"的"是一个词,比如说出现了"的确"这类的句子就不一定分得出来了。
经过以上分词规则过滤后的chunk就是最后分词的结果(从规则1开始,直到只有一个chunk时截止)。最后原本想介绍一下mmseg c实现中最核心部分的代码,因为实现代码太过复杂,不得不放弃之。想挑战的同学可以去看看,鉴于目前流行的中分分词算法都是基于词典来实现的,所以这里不再介绍基于统计概率算法的相关知识。