大数阶乘的实现
当提到计算一个数的阶乘时,也许很多人都能够轻易的解决,但很多人可能会发现,当计算100或200甚至更大的数的阶乘时,发现一般的方法无法实现,因为就拿200来说,200的阶乘的最后结果的位数达375位,一般的数据类型(如int)根本无法存储,那就得采用其他的方法来解决。
说到这里,可能有人已经想到了,没错,这与求任意位数Pi值及大整数运算的思想都是相似的,即:采用数组来存储。
关于计算任意位数Pi值及大整数运算的方法,可参见我的博客:
计算任意位数Pi值 、大整数运算
好,我们先来看一看一般的方法求阶乘:
(1)递归实现(常用)
代码:
/************************************************************************/
/* function: 计算阶乘(递归实现)
auther: ZhangYachao
blog:http://blog.csdn.net/u012027907 */
/************************************************************************/
int factorial(int n)
{
if(n <= 1)
return 1;
else
return n*factorial(n-1);
}
(2)非递归实现
代码:
/************************************************************************/
/* function: 计算阶乘(非递归实现)
auther: ZhangYachao
blog:http://blog.csdn.net/u012027907 */
/************************************************************************/
int Factorial(int n)
{
int result = 1;
for(int i = 1; i <= n; i++)
{
result *= i;
}
return result;
}
以上两种方法只能求12以内的阶乘,因为为int型,当然是用long int能够求再大点的,但仍然无法求200或更大的数。接下来我们来看看大数的阶乘实现思想:
当计算结果超出了变量值的范围,我门就采用数组来存储。
例如5的阶乘:
5
* 4
------------------------
2 0
我们用数组result[5]来存储,则result[3] = 2, result[4] = 0;
2 0
* 3
-------------------------
6 0
此时result[4] = 0;result[3] = 6 ;
6 0
* 2
-----------------
1 2 0
result[4] = 0; result[3] = 12;此时需要进位,即本位为result[3] % 10 = 2; 进位数为:pos = result[3] /10;
result[2] = pos = 1;
照此方法即可求得大数的阶乘!
代码:
/************************************************************************/
/* function: 计算大数阶乘
auther: ZhangYachao
blog:http://blog.csdn.net/u012027907 */
/************************************************************************/
void carry(int bit[],int pos) //计算进位
{
int i,carray = 0;
for(i = 0; i <= pos; i++) //从0-pos逐位检查是否需要进位
{
bit[i] += carray; //累加进位
if(bit[i] <= 9) //小于9不进位
carray = 0;
else if(bit[i] > 9 && i < pos) //大于9但不是最高位
{
carray = bit[i]/10; //保存进位值
bit[i] = bit[i]%10; //得到改位的一位数
}
else if(bit[i] > 9 && i >= pos) //大于9且是最高位
{
while(bit[i] > 9) //循环向前进位
{
carray = bit[i]/10; //计算进位值
bit[i] = bit[i]%10; //当前的一位数
i++;
bit[i] = carray;
}
}
}
}
int BigDataFactorial()
{
int num,pos,digit,i,j,m,n;
double sum = 0; //计算阶乘结果的位数
int *fact; //保存阶乘结果的指针
printf(" 请输入计算阶乘的数:Num = ");
scanf("%d",&num); //输入计算阶乘的数
for(i = 1; i <= num; i++) //计算阶乘结果的位数
sum += log10(i);
digit = (int)sum + 1; //数据长度
if(!(fact = (int*)malloc((digit+1)*sizeof(int)))) //分配保存位数的内存
{
printf("分配内存失败!\n");
return 0;
}
for(i = 0; i <= digit; i++) //初始化数组
fact[i] = 0;
fact[0] = 1;
for(i = 2; i <= num; i++) //将2-num逐个与原来的数相乘
{
for(j = digit; j >= 0; j--) //查找最高位
{
if(fact[j] != 0)
{
pos = j;
break;
}
}
for(j = 0; j <= pos; j++)
fact[j] *= i; //每一位与i相乘
carry(fact,pos); //进位处理
}
for(j = digit; j >= 0; j--) //查找最高位
if(fact[j] != 0)
{
pos = j;
break;
}
m = 0;
n = 0;
for(i = pos; i >= 0; i--) //输出计算结果
{
printf("%d",fact[i]);
m++;
if(m % 5 == 0) //每5个数字空一格
printf(" ");
if(40 == m) //每行输出40个数字
{
printf("\n");
m = 0;
n = 0;
/* n++;
if(10 == n) //每输出10行暂停
{
getch(); //按任意键继续
printf("\n");
n = 0;
}
*/
}
}
printf("\n\n");
printf("%d的阶乘共有%d位。\n",num,pos+1);
return 1;
}
void main()
{
int n = 5;
int result;
result = factorial(n);
printf("递归计算%d的阶乘:%d\n",n,result);
result = Factorial(n);
printf("非递归计算%d的阶乘:%d\n\n",n,result);
BigDataFactorial();
}
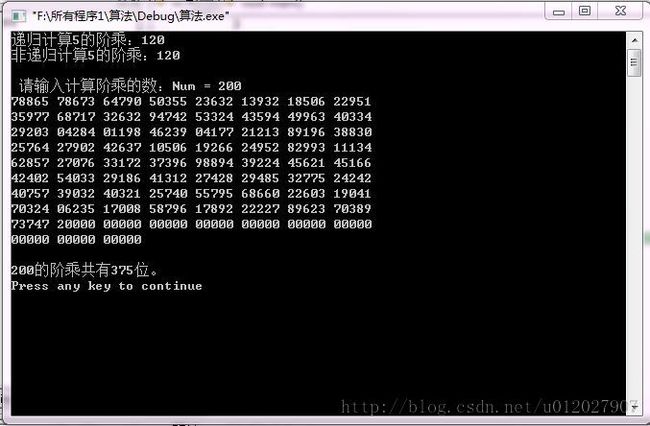
运行截图:
参考《零基础学算法》
转载请标明出处:http://blog.csdn.net/u012027907