计算任意位数的Pi

    当用程序实现求pi的值时，也许你能够很快写出算法（利用求pi的几个公式），但是由于使用单变量保存结果，限于计算机硬件对变量的表示范围有限，因此，最多只能计算出pi值小数点后十多位。但需要得到一个更大位数的pi值时，就得考虑其他的算法。

   我们采用这个公式计算pi： pi/2 = 1+1/3+1/3*2/5 + 1/3*2/5*3/7 + 1/3*2/5*3/7*4/9+......

   在计算上述公式的个分式值时，由于1/3这类的分数是无限循环小数，而使用单变量时，由于变量能表示的范围有限，因此，多余的部分将被舍去。为了提高精度，这时可以定义数组来逐位保存无限循环小数，例如：定义有20个元素的数组temp,每个元素保存一位数，则2/3的结果讲师如下效果：

位0                              位19

    6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6

则

  2/3 * 2/5

可按以下方式计算：

（1）由于2/3的结果以保存在数组temp中，用分数2/5的分子2去与数组temp的各个元素相乘，并将结果保存到temp个元素中。

（2）对数组temp个元素进行进位处理。

（3）用数组temp个元素除以分母5，并将结果保存到对应的数组元素中。在使用数组temp中的元素进行除法运算时，将从数组的低位（序号0）开始。首先用temp[0]的值除以5，列出其除法竖式如下：

            1

        5 [  6

            5

            1

   得到的商为1，则将商保存在数组temp[0]中，接着将余数1乘以10累加到下一个元素temp[1]中，使temp[1]的值变为16.用temp[1]的值16除以5，得到商为3，将商保存到temp[1]中，余数为1，将其乘以10累加到下一个元素temp[1]中，......,这样不断地重复，最后使temp数组变为如下形式：

位0                                            位19

    1  3  3  3  3  3  3  3  3  3  3   3 3 3  3  3  3  3

（4）通过上面的操作，完成了一个数列的计算，并按位保存到数组temp中，再将temp数组中的值累加到pi数组中。

不断重复上述过程，即可得到指定位数的pi值。

提示：由于数列可以不断重复，什么时候终止循环哪？当数组temp中的值全为0,则表示已经没有余数需要处理；如果数组中的元素一直不为0,就需要设置另外的条件来终止循环，如规定循环处理的次数。

计算任意位数Pi值的程序代码：

#include <stdio.h>
/* function: 计算任意位数pi值
   auther: ZhangYachao
   blog:http://blog.csdn.net/u012027907
 */
void CaculatePi()
{
	int len,i;                   //len为小数长度
	int numberator = 1,denominator = 3,result,carry;
	int flag = 1,count = 0;      //继续循环的标志及循环的次数
	char *pi,*temp;              //指向保存pi值和临时计算结果的数据
	printf("请输入小数位数：");
	scanf("%d",&len);
	
	len += 2;   //增加两位
	if(!(pi = (char*)malloc(sizeof(char)*len)))   //分配保存pi值的内存
	{
		printf("分配内存失败！\n");
		exit(0);
	}
	if(!(temp = (char*)malloc(sizeof(char)*len))) //分配保存呢临时值的内存
	{
		printf("分配内存失败！\n");
		exit(0);
	}

	for(i = 0; i < len; i++)  //初始化数组
	{
		pi[i] = temp[i] = 0;
	}
	pi[1] = 2;         //置初值
	temp[1] = 2; 

	while(flag && (++count < 2147483647))  //int的最大值 2147483647
	{
		carry = 0;
		for(i = len-1; i > 0; i--)     //从低位到高位相乘
		{
			result = temp[i] * numberator+carry; //用每一位去乘，再加上进位
			temp[i] = result % 10;               //保存个数
			carry = result / 10;                 //进位
		}

		carry = 0;
		for(i = 0; i < len; i++)                 //有高位到低位进行除法运算
		{
			result = temp[i] + carry*10;         //当前位加上前一位的余数
			temp[i] = result / denominator;      //当前位的整数部分
			carry = result % denominator;        //当前位的余数，累加到下一位的运算
		}
		flag = 0; //清除标志

		for(i = len-1; i > 0; i--)               
		{   
			result = pi[i] + temp[i];            //将计算结果累加到result中
			pi[i] = result % 10;                 //保留一位
			pi[i-1] += result / 10;              //向高位进位
			flag |= temp[i];                     //若temp中的数全为0,退出循环
		} 
		numberator++;       //累加分子
		denominator += 2;   //累加分母
	}
	printf("\n计算了%d次\n",count);              //输出循环次数
	printf("\t--- 第1-1000为小数----\n");
	printf("PI = \n");
	printf("%d.",pi[1]);
	for(i = 2; i < len; i++)
	{
		if((i>2) && (i-2)%10 == 0)        //每10位小数间加一个空格
			printf(" ");
		if((i>2) && (i-2)%50 == 0)       //每50位小数换行
			printf("\n"); 

		printf("%d",(int)pi[i]);         //输出一位小数
	}
	printf("\n");

}
void main()
{
	CaculatePi();
}

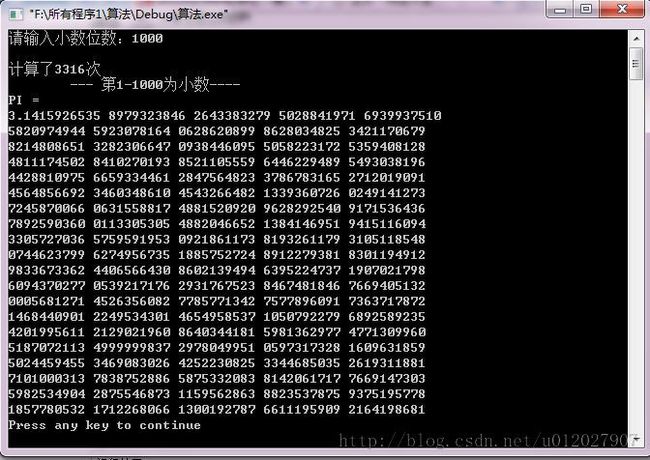
运行结果:

参考《零基础学算法》

转载请标明出处：http://blog.csdn.net/u012027907