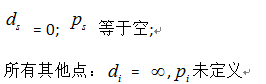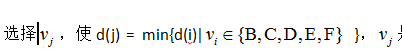最短路径之迪杰斯特拉算法（Dijkstra）

1.迪杰斯特拉（dijkstra）算法简介

Dijkstra算法是由E.W.Dijkstra于1959年提出，又叫迪杰斯特拉算法，它应用了贪心算法模式，

是目前公认的最好的求解最短路径的方法。算法解决的是有向图中单个源点到其他顶点的最短

路径问题，其主要特点是每次迭代时选择的下一个顶点是标记点之外距离源点最近的顶点。但

由于dijkstra算法主要计算从源点到其他所有点的最短路径，所以算法的效率较低。

2.dijkstra算法基本过程

假设路网中每一个节点都有标号 是从出发点s到点t的最短路径长度；表示从s到t的最短路径中t点的前一个点。求解从出发点s到点t的最短路径算法的基本过程为：

1.      初始化。出发点设置为：

 

标记起源点s，记k = s,其他所有点设为未标记。

2.      检验从所有已标记的点k到其他直接连接的未标记的点j的距离，并设置:

3.      选取下一个点。从所有未标记的点中选取 最小的点i，点i被选为最短路径中的一点，并设为已标记的。

4.      找到点i的前一点。从已经标记的点集合中找到直接连接到点i的点,并标记为 。

5.      标记点i。如果所有的点已标记，则算法结束。否则，记k = i，转到2继续。

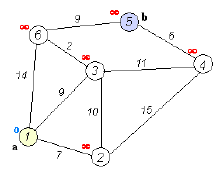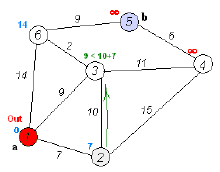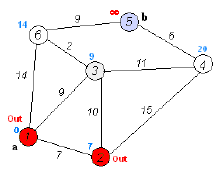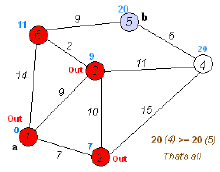
如下图：

从以上算法的步骤中可以看出 ：dijkstra算法的关键部分是从未标记的点中不断地找出距离源点距离最近的点，并把改点加入到标记的点集合中，同时更新未标记的点集合中其余点到起始点的最短估计距离[z1] 。

以一个带有权值的无向图为例，用dijkstra算法分析从源点A到目标点F的最短路径。

1. 用带有权值的一个矩阵w表示含有n各节点的带权无向图， 代表弧段 的权值，如果从节点 到节点 不连通，那么 ，带权值图邻接矩阵如下图所示.设置A为源点,G为目的点, 代表从节点A到有向图中其他节点 的最短路径长度。设置初始值代表标记的节点集合。

2. 是从A点出发求出的一条最短路径上的终止节点，令 ；

3.  修改起始节点A到集合之间的最短路径的长度值，如果d(j)+w(j,k) < d(k)，那么d(k) = d(j) + w(j,k)；

4. 重复步骤2、3的操作N-1次，最终得到从起始节点A到其他节点的最短路径，按照递增的顺序排列路径的长度。

3.dijkstra算法的流程图如下所示：

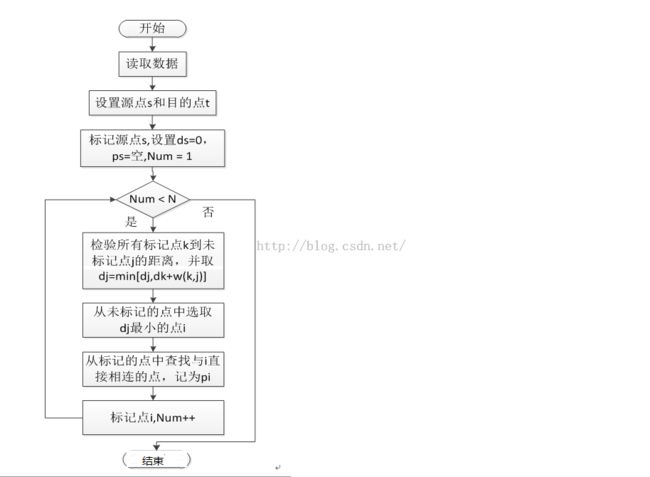
4.代码段如下：

//dijkstra(迪杰斯特拉)算法
//杨鑫
#define MAXVEX 9
#define INFINITY 65535
typedef int Patharc[MAXVEX];				//用于存储最短路径下的数组
typedef int ShortPathTable[MAXVEX];			//用于存储到各点最短路径的权值和
/*Dijkstra算法，求有向图G的V0顶点到其余顶点V最短路径P[v]及带权长度D[V]
 *P[V]的值为前驱顶点下标，D[V]表示V0到V的最短路径长度和
 * */
void Dijkstra(MGraph G, int V0, Patharc *P, ShortPathTable *D)
{
	int v, w, k, min;
	int final[MAXVEX];			//用于标记
	/*初始化*/
	for(v = 0; v < G.numVertexts; v++)
	{
		final[v] = 0;
		(*D)[v] = 0;
		(*P)[v] = 0;
	}
	(*D)[v0] = 0;
	final[v0] = 1;				//把v0标记为1后就不再搜索v0，下一行的循环从v1开始
	/*循环，每次求得v0到某个v顶点的最短路径*/
	for(v = 1; v < G.numVertexts; v++)
	{
		min = INFINITY;
		for(w = 0; w < G.numVertexes; v++)
		{
				if(!final[w] && (*D)[w] < min)
				{
					k = w;
					min = (*D)[w];							//w顶点离v0顶点更近
				}
		}
		final[k] = 1;							//找到一个顶点，就把标记为一，下次就不搜索该顶点
		for(w = 0; w < G.numVertexes; w++)
		{
			if(!final[w] && (min + G.arc[k][w] < (*D)[w]))
			{
				(*D)[w] = min + G.arc[k][w];
				(*p)[w] = k;
			}
		}
	}
}