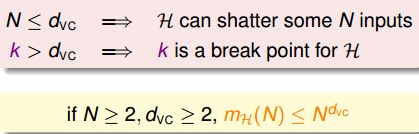机器学习基石——第7-8讲.The VC dimension

本栏目（机器学习）下机器学习基石专题是个人对Coursera公开课机器学习基石（2014）的学习心得与笔记。所有内容均来自Coursera公开课Machine Learning Foundations中Hsuan-Tien Lin林轩田老师的讲解。（https://class.coursera.org/ntumlone-002/lecture）

第7讲-------The VC dimension

一、VC dimension的定义

VC dimension是什么呢？大家可能猜到了，这是和我们上次讲的VC bound是有些关系的。我们试图给我们之前一直围绕着讲的break point一个正式的名称：the formal name of maximum non-break point。所以可以认为d_vc = 'minimum k' - 1。 

想象一下，如果N<=d_vc，则存在某个D会被hypothesis shatter。表示训练数据有可能被hypothesis shatter到，但是不一定；如果N>d_vc，则可以肯定的是它一定不能被shatter到。

所以，我们之前说，拥有break point露出一线曙光的是好的hypothesis。现在有了VC dimension的新概念之后，则变成了d_vc是finite有限的时候。Ok，接下来做一个题目巩固一下：

参考答案是我们不知道。我们只有看到N笔数据没办法被shatter住，如果有另外N笔数据可以被shatter，那么VC dimension就会>=N了；如果其他的N笔数据通通都不能被shatter，那么VC dimension就要比N来的小。

二、Perceptron的VC dimension

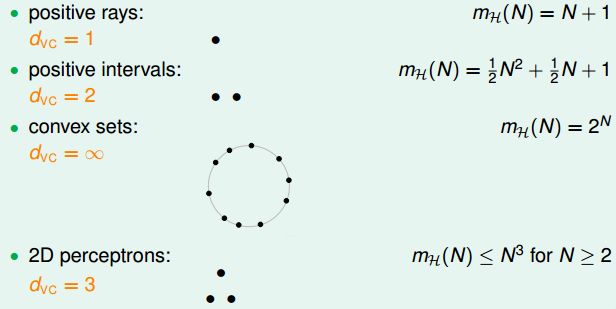
那么，对于多维的数据时，感知机到底又会如何呢？我们回想一下，1维感知机d_vc = 2；2维感知机d_vc = 3。那是否多维感知机d_vc = d + 1呢？要证明这个假设，需要分d_vc >= d+1以及d_vc <= d+1两步。

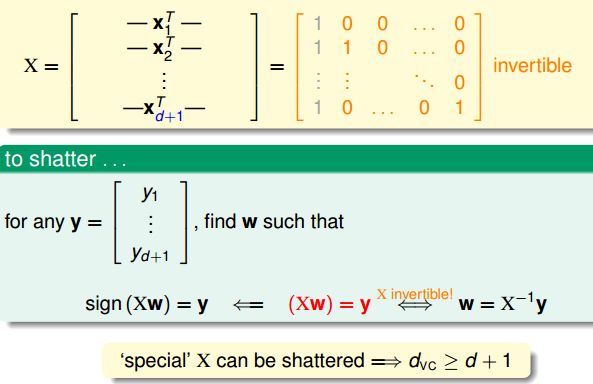
第一步：d_vc >= d+1。也就是说，存在某个d+1维的数据能够shatter住。选择如下一个特殊的数据X，可以认为是单位矩阵加上原点共d+1维，左侧第一列灰色的1则是加入的x0常数，我们接下来想证明这个d+1维的数据是可以shatter的。

我们说的shatter在数学上表示则为，我们给出任何一种圈圈叉叉的排列组合y，都存在w满足sign(Xw) = y。因为X的逆矩阵存在，这样的w是可以求解的，总共有2^(d+1)这么多种y的可能性。这样就证明了这个d+1维的数据时可以shatter的，所以d_vc >= d+1。

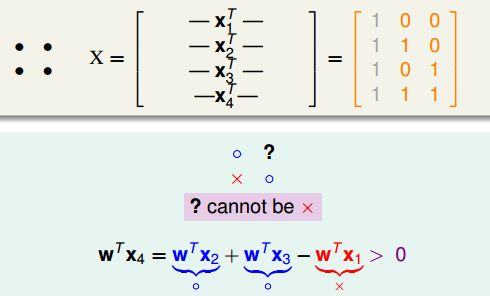
第二步：d_vc <= d+1。也就是说，任何d+2维的数据都不能被shatter住。先回到2维特殊的例子，不能shatter的情形就是4个点。原来说过，如果左上角和右下角的点如果是圈圈、左下角的点是叉叉，我们会发现？位置的点是无法为叉叉的，这样的dichotomy是没有办法产生。从数学上来讲，向量x4可以通过x1、x2、x3的线性组合来表示，即x4 = x2 + x3 - x1，如果左右两边同时乘以w如下图所示，那么w^Tx4一定>0，也就是一定为圈圈，不能为叉叉。由此可见，线性依赖的关系会限制可以产生dichotomy的数量。

更一般的情况来说，如果有d+2维的数据，由于列数是d+1，所以根据线性代数的知识x_d+2可以表示为前d+1个x的线性组合。那么一定无法产生这样的一个dichotomy：(sign(a1), sign(a2), ... , 叉叉)。也就是说，d+2个点是不能够shatter的。所以d_vc >= d+1。

三、VC dimension的物理意义

我们发现，d+1实际上就是perceptron的维度，所以VC dimension就和perceptron的维度联系起来了。hypothesis set是由d+1维的w来表示的，而这些w可以代表着hypothesis的自由度degrees of freedom。所以VC dimension的物理意义就是effective ‘binary’ degrees of freedom，hypothesis set在作二元分类的状况下到底有多少的自由度。同时也就象征着powerfulness of H，到底能够产生多少的dichotomies。

也就是说，VC dimension大体上代表着我们有多少可以调的参数。这个假设大致是对的，不过不是总是对的。不过实际应用中，如果要大致估计VC dimension是多少的话，通常可以看看有多少可以调节的参数。看看如下的训练题，经过原点的超平面的d_vc应该是多少。使用刚刚上面讲到的一模一样的证明可以得到d_vc就是d，不过我们其实可以直观地想一下，我们共有d+1个参数，不过w0是没法调节的，也就是说实际上只有d个有效的参数。

d_vc很小的时候，发生坏事情的概率就小，但是limited power；而d_vc很大的时候，拥有lots of power，但是发生坏事情的概率就大。因此，实际应用中选择合适的d_vc的hypothesis set就变得很重要了。

四、深入了解VC dimension的意义

VC dimension的一种意义是表征着model complexity。为了更深刻的了解VC dimension的意义，我们将的VC bound更换一种表达形式：坏事情发生的机会会很小为δ。那么，反过来我们描述好事情发生的概率则应该很大，>= 1 - δ。那么可以一路代换得到ε，也就是说有很大的机会E_in(g)和E_out(g)会被限制在ε内。那么就可以得到E_out(g)的confidence区间就是E_in(g) ± ε。

ε通常称为penalty of model complexity Ω(N, H, δ)。model当然指的就是hypothesis set，它所要付出的代价，样本数量、d_vc是多少、坏事发生的小概率δ。也就是说，我们可以把Learning发生的事情大概画成如下的图。in-sample error为E_in(h)，out-of-sample error则为E_out(h)它们随着VC dimension的变化。d_vc变大，可以shatter的点就变多了通常E_in(h)会变小，E_out会是一个先下降后上升的过程，受到model complexity上升的影响。所以，最好的d_vc是在中间的位置，powerful H not always good!

其实，VC bound还有另外的一种含义：Sample Complexity样本复杂度。在给定其他指标在一定期望范围内的时候，想知道到底需要多少的训练数据。通过计算会发现，理论上需要的训练数据量会是1w倍的d_vc那么多；不过实战中，一般只需要10倍d_vc的数据量就能达到还不错的效果。

这样看来VC bound是非常宽松的，那么宽松的来源是什么？首先，Hoeffding确保我们对任何的distribution和target不需要知道P和f都可以用这个bound来确保；其次，用Growth Function代替hypothesis set的dichotomy真正的数量，确保可以使用任何的训练数据而不只是某一个抓在手上的数据；再次，用d_vc的一个多项式代替Growth Function，也就是上限的上限，确保了有相同vc dimension任何的hypothesis set都可以使用；还有，在最坏的情况下进行union bound，确保在最坏情况下也能有效。

第8讲-------The Noise and Error

上一届介绍了机器学习中很重要的一个概念，VC dimension，本节的主题是在有噪声的情况下我们如何衡量这些错误。

一、Noise and Probabilistic target

噪声是容易出现的，人工标记错误；同一个数据不同人工标记不同；训练数据收集可能不精准等等原因。那么在有噪声的时候，我们之前推导的VC bound是否仍然能作用的很好？

回想一下，VC bound的核心：我们不知道一个罐子里有多少橘色的弹珠，不过我们抓一把出来就可以估计橘色的弹珠有多少，这些橘色的弹珠就是我们犯错误的地方。噪声的影响就是特别的弹珠，弹珠的颜色不是固定的，譬如弹珠40%是橘色的，60%的时候是绿色的。那这时候我们如何知道罐子大致的橘色的比例是多少呢。

也就是说，只要我们的每个训练数据y来自某一个joint distribution P(y|x)，我们在训练的时候和测试的时候都符合P(y|x)，那么这个VC bound的大架构还是有效的。P(y|x)通常叫做target distribution，对于每一个x可以做一个它最理想的预测‘mini-target’是什么。它告诉我们最理想的预测'ideal mini-target'是什么，另外不理想的就是noise。例如P(o|x) = 0.7, P(x|x) = 0.3，也就是说现在拿了一颗弹珠它是圈圈概率是0.7，请问你是要猜圈圈还是要猜叉叉。当然最好猜它是圈圈，那么错误率就是0.3。那么之前固定的target f可以认为是目前target distribution的一种特例，这时候P(y|x) = 1 for y = f(x)也就是完全没有噪声。使用target distribution的时候和之前是用target function的时候基本上没有什么太大的不一样，所以回头来看，我们Learning的目标分为两个部分了predict ideal mini-target(w.r.t. P(y|x)) on often-seen inputs(w.r.t. P(x))，一个是原先的P(x)，它告诉我们哪些点是重要的常常会被抽样到也就是在E_in(h)里经常出现；另外一个是P(y|x)，它告诉我们最理想的mini-target是什么。在常见的点上的预测要做的表现好，这就是machine learning做的事情。

二、错误衡量

如何衡量g跟f是长的很像的呢？之前使用的是E_out(g)，有三个特性：out of sample衡量的是还没有看过或者是未来抽样出来的x，point-wise可以在每一个x上个别衡量，最后做抽样的平均就可以了，classification二元分类考虑的就是对或者不对。实际上有很多的错误衡量的方式，不过为了简单起见大部分的主要集中在point-wise的方式。

那有哪些Point-wise的错误衡量方式呢？0/1 error通常用在分类上，分对还是分错；平方的error通常用在回归分析，计算错误的距离。未来会讲更多不同错误衡量方式。不同的错误衡量方式，会影响到最理想的mini-target，也就是最好的f会长什么样。

VC理论对于很多不同的hypothesis set还有很多不同的错误衡量方式来说都会work。也就是说，不管是classification还是regression，不只是0/1的错误衡量，都能得到类似的VC bound。详细的数学推导太过于繁复，大家没有必要都走过一遍。

三、算法中错误衡量的选择

这些错误的衡量到底哪里来的呢？想象一个指纹分类系统，分类器可能会犯两种错误：false accept，应该要说不可以用，但是分类器说可以用；false reject，明明应该可以用，但是分类器说不可以用。其实也就是我们在分类中常说的 false positive 和 false negative，只是台湾和大陆的叫法不同而已。对于这两种错误的类型，之前的0/1 error penalizes both types equally。然而，在实际应用中，两种错误带来的影响可能很不一样。

例如，一个商场对顾客进行分类，老顾客可以拿到折扣，新顾客没有折扣。这时，如果发生false reject（将老顾客错分为新顾客）而不给其打折，那么会严重影响用户体验，对商家口碑造成损失，影响较坏；而如果发生false accept （将新顾客错分为老顾客)而给其打折，也没什么大不了的。另一个例子，CIA 的安全系统身份验证，如果发生false accept（将入侵者错分为合法雇员），后果非常严重。

通过上述两个例子，我们知道，对于不同application，两类错误的影响是完全不同的，因此在学习时应该通过赋予不同的权重来区分二者。比如对于第二个例子，当发生false accept时对E_in 加一个很大的权重。因此，error is application/user-dependent.

但是很多时候错误衡量的具体权重是不太能确定的，所以在设计算法的时候常常要采用替代的方式。一种替代方式是找一些有意义的错误衡量，例如之前Pocket PLA在进行0/1分类时如果分不对就认为是噪声，想办法让噪声最小也就是0/1 error最小（NP hard问题之前有提到）。以及以后会讲到的距离平方的方式，想办法高斯噪声最小；另外一种替代方式会更friendly，例如很容易求出解，或者凸优化的目标函数等。

 四、带权重的分类

借助上面的CIA 身份验证的例子来说明什么是weighted classification。

通过感知机模型解决CIA 分类问题。如果数据时线性可分的，那么带权重与否对结果没有影响，我们总能得到理想结果。如果输入数据有噪音（线性不可分），像前面学习感知机时一样，采用Pocket 方法的修改版本，每一次迭代尝试去找比当前加权的E_in(h)更小的超平面，计算错误时对待两种错误(false reject/false accept) 不再一视同仁，false acceot 比false reject 严重1000倍。这个Pocket的修改版本真的有理论上的保证吗？

一种比较机械的方式就是，在训练开始前，我们将{(x,y) | y=-1} 的数据复制1000倍之后再开始学习，后面的步骤与传统的pocket 方法一模一样。然而，从效率、计算资源的角度考虑，通常不会真的将y=-1 的数据拷贝1000倍，实际中一般采用"virtual copying"。只要保证：randomly check -1 example mistakes with 1000 times more probability。也就是说，随机访问-1错误点的几率在概率上要比非权重PLA算法时访问-1错误点的几率高了1000倍。

总之，我们选择好适合特定应用的error measure: err，然后在训练时力求最小化err，即，我们要让最后的预测发生错误的可能性最小（错误测量值最小），这样的学习是有效的。

 

关于Machine Learning Foundations更多的学习资料将继续更新，敬请关注本博客和新浪微博Sheridan。

原创文章如转载，请注明本文链接: http://imsheridan.com/mlf_7th_lecture.html