二叉树的遍历

知识点扼要回顾：
所谓二叉树的遍历，是指按一定的顺序对二叉树中的每个结点均访问一次，且仅访问一。按照根结点访问位置的不同，通常把二叉树的遍历分为六种：
TLR（根左右）, TRL（根右左）, LTR（左根右）
RTL（右根左）, LRT（左右根）, RLT（右左根）

其中，TRL、RTL和RLT三种顺序在左右子树之间均是先右子树后左子树，这与人们先左后右的习惯不同，因此，往往不予采用。余下的三种顺序TLR、LTR和LRT根据根访问的位置不同分别被称为前序遍历、中序遍历和后序遍历。

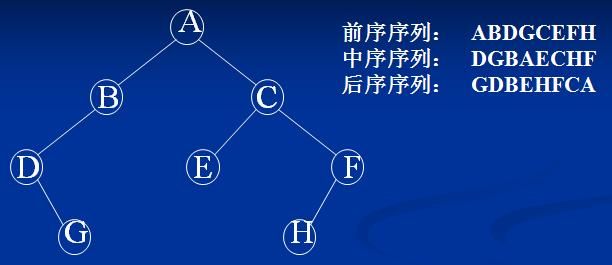
前序遍历的规律是：输出根结点，输出左子树，输出右子树；  
中序遍历的规律是：输出左子树，输出根结点，输出右子树； 
后序遍历的规律是：输出左子树，输出右子树，输出根结点；

举例：

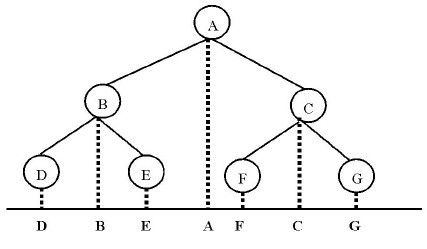
特别的，根据文献 袁宇丽的《数据结构中二叉树中序遍历的教学分析》，讲到中序遍历的另外一种方法，即投影法，如下图所示：

  

所以中序遍历的结果是：DBEAFCG。

我认为也可以根据下面的递归算法来理解3种遍历方式。

以下转自：http://blog.sina.com.cn/s/blog_60281b700100dmg1.html

一、问题需求分析

利用程序建立一个二叉树，并实现各种遍历算法。

一、问题需求分析
利用程序建立一个二叉树，并实现各种遍历算法。
 
二、算法选择
二叉树的建立
二叉树建立的方法有很多种，最常用的是采用递归的先根次序来建立，这次的实验就是采用此算法。
二叉树的遍历
二叉树的遍历有常用的三种方法，分别是：先根次序、中根次序、后根次序。为了验证这几种遍历算法的区别，本次的实验将会实现所有的算法。
遍历的时候，把结点的信息打印出来，为了让结点的信息更容易区别，在每个结点前加上数字标识。如：data[1]=A,data[2]=B.
实现的算法皆为递归算法。
 
三、分情况处理的实现
由于算法需要同时实现出来字符型数据和整形数据，这两种数据处理过程中，对输入和输出的处理会有所不同，为了实现这个功能，采用#ifdef和#else的代码选择方法。
代码示例：
#define CHAR
//为了增强程序的多功能，定义CHAR时，用字符的处理模式
//当CHAR没有被定义时，采用整数处理模式
#ifdef CHAR
//数据类型的定义
typedef char datatype;
#else
typedef int datatype;
#endif
更详细的代码请看后面的代码汇总
 
四、程序代码
//二叉树的实现算法
//**BY 祥泰
//**09-6-6
 
#include<stdio.h>
#include<stdlib.h>
 
#define CHAR
//为了增强程序的多功能，定义CHAR时，用字符的处理模式
//当CHAR没有被定义时，采用整数处理模式
//数据类型的定义
#ifdef CHAR
typedef char datatype;
#else
typedef int datatype;
#endif
 
typedef struct node
{
   datatype data;
   struct node *lchild,*rchild;
}bitree;
bitree *root;
int n;
char c;
 
//创建二叉树
bitree *creat_preorder()
{
   bitree *t;
   datatype x;
 
   #ifdef CHAR
   printf("\n\t\t请输入字符，以0作为每个节点的结束标志:");
   scanf("%c",&x);
// fflush(stdin);//清除缓冲区
   while((c=getchar())!='\n'&&c!=EOF);  //清除缓冲区另外的方法
   if(x=='0')t=NULL;
   #else
   printf("\n\t\t请输入正整数以0作为结束标志:");
   scanf("%d",&x);
   if(x==0)t=NULL;
   #endif
 
   else
   {
      t=(struct node *)malloc(sizeof(bitree));
      t->data=x;
      t->lchild=creat_preorder();
      t->rchild=creat_preorder();
   }
   return(t);
}
 
//先根遍历算法
void preorder(bitree *t)
{
   if(t!=NULL)
   {
      n=n+1;
      #ifdef CHAR
      printf("\tdata[%2d]=%3c",n,t->data);
      #else
      printf("\tdata[%2d]=%3d",n,t->data);
      #endif
      if(n%5==0)printf("\n");
      preorder(t->lchild);
      preorder(t->rchild);
   }
}
 
//中根遍历算法
void  inorder(bitree *t)
{
   if(t!=NULL)
   {
      inorder(t->lchild);
      n=n+1;
      #ifdef CHAR
      printf("\tdata[%2d]=%3c",n,t->data);
      #else
      printf("\tdata[%2d]=%3d",n,t->data);
      #endif  
      if(n%5==0)printf("\n");
      inorder(t->rchild);
   }
}
 
//后根遍历算法
void postorder(bitree *t)
{
   if(t!=NULL)
   {
      postorder(t->lchild);
      postorder(t->rchild);
      n=n+1;
      #ifdef CHAR
      printf("\tdata[%2d]=%3c",n,t->data);
      #else
      printf("\tdata[%2d]=%3d",n,t->data);
      #endif  
      if(n%5==0)printf("\n");
   }
}
 
main()
{
   bitree *bintree=creat_preorder();
   printf("\n先根序列：\n\n");
   preorder(bintree);
   n=0;
   printf("\n中根序列：\n\n");
   inorder(bintree);
   n=0;
   printf("\n后根序列：\n\n");
   postorder(bintree);
   n=0;
   printf("\n\n");
 
}
 
五、测试前的说明
测试之前要简单介绍一下建立二叉树的方法，即怎样把一棵二叉树输入程序当中。
以课本中P124页的图5.6作为例子说明。请看下图：


 
当要输入这个二叉树时，根据先根次序的序列，首先输入A，然后是左子树B，然后以B作为结点，再输入B的左子树D，由于D没有分支了，所以用0作为填充表示后面没有分支了，如右图所示的虚线结点，因此，D后面都是输入0，0。接下来返回，输入B的右子树，也为0。依此类推，则图5.6中的二叉树的数据输入次序为：A B D 0 0 0 C E 0 G 0 0 F H 0 0 I 0 0 。
了解了输入的方法后，下面开始测试啦。(*^__^*)
 
六、程序测试
1、 字符型数据测试
首先在编译程序前，在程序的开通先定义CHAR。生成EXE文件后就可以测试了。
按上面课本中的二叉树作为测试数据。数据输入次序为：A B D 0 0 0 C E 0 G 0 0 F H 0 0 I 0 0 。每输个数按一次回车。 
录入的过程：
 


 
录入完毕后的输出结果：


 
可见，测试的序列和课本给出的序列是相同的，测试通过。
 
2、 整型数据测试
首先把程序中的#define CHAR这句屏蔽掉，重新编译程序，生成EXE文件。
跟字符型的数据类似，只不过输入和输出的数据格式不一样而已。
下面是测试的结果，把上面的二叉树的字符转变为ASCII码输入的。
 
 
程序测试正确。
 
七、有待改进的问题和体会
这个程序的代码较为简单，可以实现了二叉树的三种遍历算法，想要改进的话可以在扩充其功能上下手，例如实现更多遍历算法，建立的时候提示更人性化，对输入的数据进行有效性验证等等。
花了不少心思在代码的复用上，尽管复用的技术还不算高超，不过对于这次的实验要求来说，已经是很完美的实现了。
二叉树这个数据结构几乎在每一本的数据结构的书都作为重点内容讲述，足见其在算法和程序设计界的重要地位。但是，到目前为止，自己还没有真正体验到它的威力，可能是时机未到吧。
二叉树的数据结构很强调的观点是递归的思想，对于递归的思想，计算机处理起来是比较简单的，但对于人来说，只要递归的深度一大的话，思维就会混乱。例如，像遍历的算法，用递归的算法只是简单的几行代码，然后就可以实现输出遍历次序。但是，对于人工分析的话，是相当复杂的。
程序开始时，建立二叉树需要输入数据，而且数据是按照先根次序读取录入，这里要人工来解决，所以相当的麻烦。我是试验了很多次，才把输入的方法摸透。为了减轻别人使用程序的痛苦，我已经把数据录入的方法详细地写出来了，希望对大家有所帮助和启发，体会到开发工程师的感觉了，就是要站在客户挑剔的眼光想问题，把客户可能遇到的问题都帮他解决，就如使用说明书，程序的可复用性等等，这是产品人性化设计的一个部分，也是战胜其他竞争对手的有力法宝。
把每一次的实验当作是一次项目的开发，就会做到完全投入其中，享受开发的每一个过程。