POJ 2082 Terrible Sets
/*
这题的题目比较难读懂,其实就是给定坐标系上一系列相邻的矩形,高度不等,求把这些矩形连起来看
能够得到的最大矩形的面积.这题我一开始想到的是需要用堆栈来往后处理,但是一直想不出来Discuss
里面说的O(N)的算法,再加上昨天又是09年最后一天,实在没心情搞下去了.今天早上睡了个懒觉,起来
状态不错,一下就想出了O(N)的算法,要想达到O(N)必须对矩形进行合并.具体思路如下:
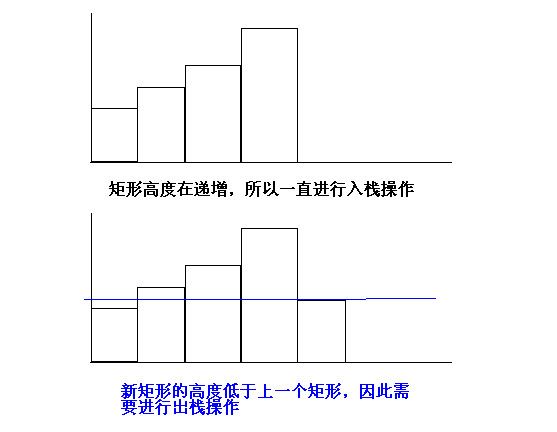
(1)设置一个堆栈用来矩形.遇到比上一个矩形高度高的新矩形就入栈
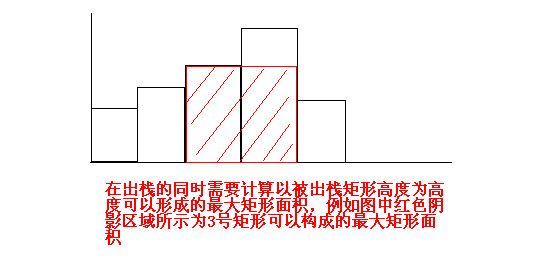
(2)如果遇到比上一个矩形高度低的矩形就要进行出栈合并以及最大矩形面积计算的处理.假设当前新
矩形的高和宽分别为curh, curw, 利用totalw统计出栈的矩形的宽度和,然后一直进行出栈操作,每出
栈一个矩形就将其宽度加到totalw上,统计将其高度乘以totalw与maxsize比较进行更新.出栈矩形的
高度乘以totalw表示的是以这个矩形的高为大矩形的高可以得到的最大矩形面积.出栈操作一直进行
到栈顶矩形的高度小于等于新矩形的高度.
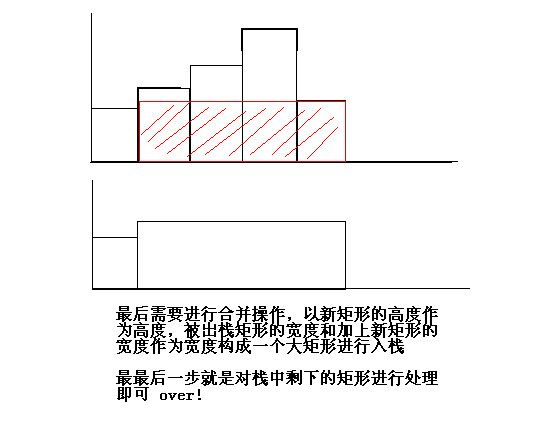
最后将新矩形的高度以及totalw + curw作为一个新的元素压入栈中.这样就完成了这种情况下对新矩形
的操作
(3)最后栈中还有一些列的矩形,这些矩形构成了一个高度非降序的矩形序列.然后再进行一边出栈处理就
可以了.可以参考图示分析.
这题整体并不难,但是确是一道非常好的题,考察对堆栈的应用以及对合并方法达到线性复杂度的理解
*/
图1:
图2:
图3:
#include <iostream>
#define MAX_N 50005
#define maxv(a, b) ((a) >= (b) ? (a) : (b))
using namespace std;
struct elem
{
int h, w;
}stack[MAX_N];
int top, n, maxSize;
int main()
{
int curw, curh, i, lasth;
while(scanf("%d", &n) && n != -1)
{
top = lasth = maxSize = 0;
int totalw , cursize;
for(i = 1; i <= n; i++)
{
scanf("%d%d", &curw, &curh);
if(curh >= lasth)
{
stack[top].h = curh;
stack[top].w = curw;
top++;
}
else
{
totalw = cursize = 0;
while(top != 0)
{
if(stack[top - 1].h > curh)
{
totalw += stack[top - 1].w;
if((cursize = totalw * stack[top - 1].h) > maxSize)
maxSize = cursize;
top -= 1;
}
else break;
}
totalw += curw;
stack[top].h = curh;
stack[top].w = totalw;
top++;
}
lasth = curh;
}
totalw = cursize = 0;
while(top != 0)
{
totalw += stack[top - 1].w;
if((cursize = totalw * stack[top - 1].h) > maxSize)
maxSize = cursize;
top--;
}
printf("%d/n", maxSize);
}
return 0;
}