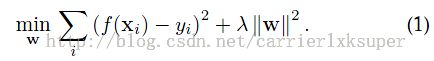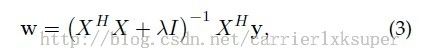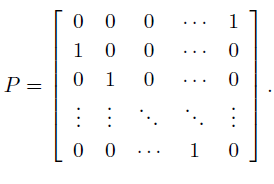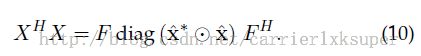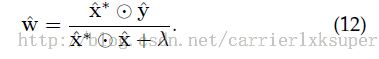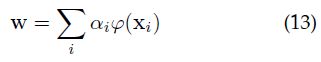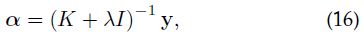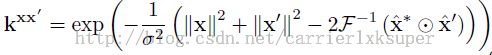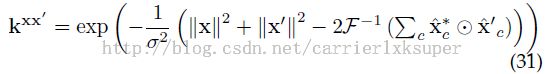High-speed Tracking with Kernelized Correlation filters笔记
最近在阅读tracking的相关文章,作为2015年的最新出的KCF ,引起我的关注,作者的相关paper以及code在此:http://home.isr.uc.pt/~henriques/circulant/
刚开始接触tracking,下面分析的可能有纰漏。在这篇文章中作者提出了一种比correlation filter更加强大的tracking方法。作者的核心思想就是:采用判别式的tracking,需要区分目标和surrounding 环境,需要大量的训练样本,这些样本之间存在着大量的冗余,于是作者采用创新的circulant matrix来生成训练样本,这样的好处就是得到的数据矩阵是circulant,于是可以利用DFT(离散傅里叶变化)对角化,从而减少计算量。 同时,作者发现用这种样本训练的linear regression 等价于correlation filter,大大加快tracking速度。同时作者考虑核regression的情况,提出了Kernelized correlation filter(KCF)以及采用线性核的Dual correlation filter。
下面将针对着上面提到的各个知识点展开。
1 Bridge regression
在tracking中,训练一个好的分类器需要大量的样本,这就意味着大量的时间消耗,作者发现很多样本之间的translation可以通过一定的方法实现,就是circulant matrices。在这里,我们选择的分类器是Bridge regression,而不是复杂的SVM,其实笔者在前几天做过实验,很多情况下,如果输入分类器的特征已经很powerful的话,两者的区别不大。笔者曾经在深度学习网络框架caffe上分别用自带的softmax分类,同时提取出倒数第二层的特征输入到SVM分类,发现精度差别很小。言归正传,在linear regression中训练的目的是找到了一个W,使得函数![]() 能够最小化样本x和目标y之间的最小二乘误差:
能够最小化样本x和目标y之间的最小二乘误差:
复数形式为
2 Cyclic shifts
在这里考虑一个一维的vector表示的是目标的一部分,我们称之为base sample。我们的目标是利用一个正的base sample和多个虚拟的负样本来训练一个分类器,这些负样本是对那个正样本的translate获得的。于是我们可以用下面的matrix实现:
对vector 做shifts的效果如下所示:
二维图像的效果如下:
表示为矩阵叫做circulant matrix就是:
这种矩阵的特性之一就是可以被离散傅里叶变换对角化:
3 替换
将公式7带入到公式3中去,![]() 可以简化为:
可以简化为:
进一步的:
括号里的正好是signal x的自相关。于是公式3可以简化为:
进一步的,
4 非线性回归(Kernel regression)
核技巧
根据表达理论,我们可以将解w表达成关于样本x的线性组合的方式:
我们将特征空间中的点积表达为:
![]()
也就是用核函数k来代表点积的运算。那么所有样本之间的点积可以存储成一个kernel矩阵K,每一个元素的形式就是:![]() .
.
于是在特征空间下,函数f(z)可以写成:
于是桥回归的解就变成了:
在这里K是核矩阵,alpha是系数矢量。如果能证明K对于数据的cyclic shifts是circulant的话那么就可以对角化公式16,因此也就大大简化计算。作者给出了很多核函数下满足上述条件。比如常见的高斯核函数,线性核等。于是上式可以对角化为下面的形式:
注意这个地方已经是频域空间中了,所有的变量都带着个hat,表明是经过DFT的。
在这里,![]() 是kernel matrix
是kernel matrix ![]() 的第一行。在这里定义核相关,指的是:
的第一行。在这里定义核相关,指的是:
5 Fast detection
为了检测感兴趣的图像位置,很多是时候需要检测多个candidate paches,这些patches可以通过cyclic shifts来建模得到。
在这里构建所有的训练样本和所有candidate patches之间的核矩阵![]() 。由于样本和patches分别是对base sample x和base patchz的cyclic shifts得到的,因此
。由于样本和patches分别是对base sample x和base patchz的cyclic shifts得到的,因此![]() 的每一个元素都可以表达成:
的每一个元素都可以表达成:![]() 。
。
在这里还需要计算这个核矩阵的第一行:
![]()
于是我们就可以得到所有 candidate patches下的回归函数:![]() ----------------------------------------21
----------------------------------------21
这里的z是一个vector,包含所有的z的cyclic shifts的输出。转化到频域就是:
直观上,最所有位置上计算f(z)等价于利用![]() 做空间滤波操作。
做空间滤波操作。
6 Fast kernel correlation
点积和多项式核
径向基函数和高斯核
7 Multi-Channel
对于HoG特征可以采用多通道的correlation filter。比如HoG特征的话,每一个patch会产生31个梯度方向bin,于是就需要对所有channel 求和之后,再处理:
最后贴出 tracking pipeline