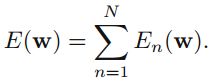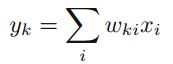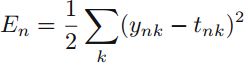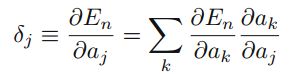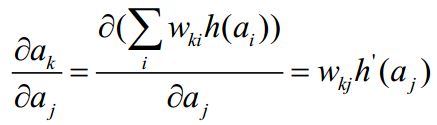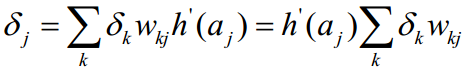神经网络（Neural Networks）

1.简介

一般的回归和分类方式是基于线性模型，也就是固定的非线性的基函数（basis function）的线性组合，形式如下：

其中，如果f（.）是非线性的激活函数（activation function），这就是一个分类模型；如果f（.）是恒等函数（identity），则是回归模型。

根据自己的认识，我认为神经网络就是多层这样的模型的叠加，并引入非线性的activation function，提高模型的整体能力（因为每一个隐藏层可以对上一层的输出进行非线性变换，因此深度神经网络拥有比“浅层”网络拥有更加优异的表达能力）。神经网络的计算量相比于其他的回归和分类模型比较大，在早期并没有受到研究者的重视，随机近几年计算机设备的性能提升从而受到广泛的关注，也诞生了新的领域Deep learning。

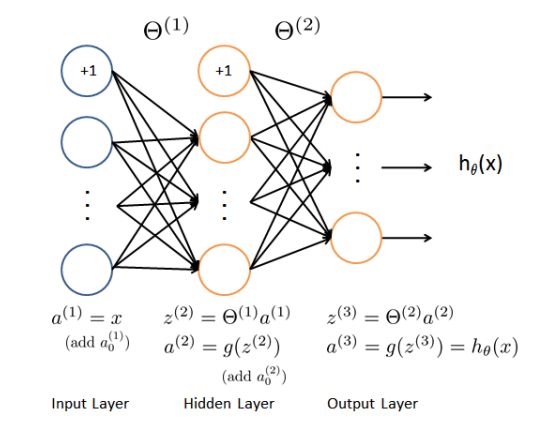
上图是简单的三层神经网络，其中，相邻层之间是全联通的（即下一层的输入是上一层所有结点的线性组合），当然也有不是全联通的网络，典型代表是卷积神经网络（CNN），CNN在计算机视觉领域取得比较的成果，由于图像的维度比较高，如果采用全联通结构会导致模型会有非常多的参数，使得模型变得非常复杂。另外，一般情况下hidden layer 的结点数目会比input layer和output layer的结点多（稀疏自动编码，是一种hidden layer的结点数比其他的小，而input layer 和 output layer的结点数相同）。

此外，神经网络也可以分为监督神经网络和非监督神经网络，我们比较熟悉的是监督神经网络，该模型可以处理分类，回归问题；非监督神经网络最典型的的就是稀疏自编码器（Sparse Autoencoder）。

神经网络主要有三部分构成：正反馈（Feedforward），代价函数（cost function）,反向传播（Backpropagation），下面从这三部分介绍神经网络。

2.正反馈（Feedforward）

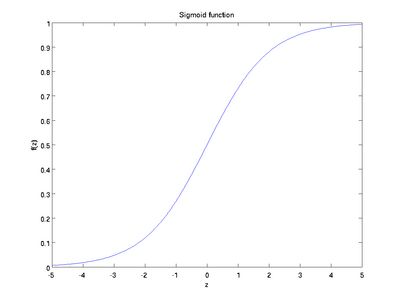
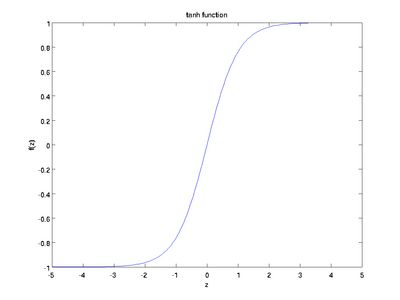
正反馈比较简单，计算过程可见上图。简单介绍下激励函数（activation function），最常用是sigmoid数和tanh函数。

sigmoid函数：

tanh函数：

这个两个函数的特性就是它的导数比较特别，方面后面的计算。Sigmoid函数的导数是，tanh函数的导数是。

3.代价函数（cost function）

在线性回归中，我们使用sum-of-square cost function，在这里我们同样可以使用，代价函数为：

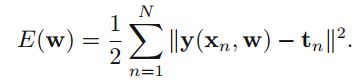
接下来，我们需要找到某个w使得代价函数最小。在回归问题中，我们可以得到参数w的解析解，但在该问题中由于activation function是非线性的，E(w)是一个非凸函数，我们无法得到解析解，但可通过迭代优化方法求解。

我们最熟悉的梯度下降（gradient descent），用梯度信息来更新参数w，每一次迭代按如下公式更新：

这是batch gradient descent，该方法的缺点是比较time-consuming，每更新一次参数需要计算整个数据集的数据。对于这种batch optimization，更高效的方法是共轭梯度（conjugate gradients）和拟牛顿（quasi-newton），这两种方法每次迭代cost function都会减小，除非w已经是局部或者全局最小值，这个和梯度下降不同。

另外一种是on-line 的方法，假设所有的观测值都是独立的，cost function 有每一个数据的cost组成：

我们采用on-line gradient descent，也被称为sequential或者stochasticgradient descent，这个方法每一次迭代都只基于一个数据数据，梯度下降中每一次迭代按如下公式更新：

Tip：为了得到足够好的最小值，我们往往需要运行多次优化算法，每一次都随机的取不同的初始参数，在validation set 上比较性能。

到目前为止，我们已经知道如何求解模型的参数了，但是cost function的梯度未知，如何求解梯度呢，神经网络通过后向传播来求解梯度，大大提高了计算效率。

4.反向传播（Backpropagation）

在这里，我以on-line的方法为例子，主要参照PRML，其中的一些符号与UFLDL 的tutorial有所不同，需要注意的是，其中z和a的意义正好相反。

现在考虑最简单的一层神经网络，也就是输出是输入的线性组合，即

，

对于某一个输入n，cost function为

，

然后我们求cost function关于wji的梯度，得到

。

现在考虑一般的神经网络结构，使用chain rule求解偏导数，得到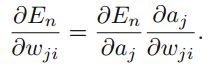，我们记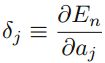，该值经常被称为error。由于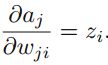，推到可以得到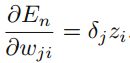。现在，我们只需要知道delta_j和z_j，就可以求解cost function关于wji的偏导数了。

输出层（output layer）

对于输出层（output layer），我们可以得到（这个自己也还没搞定，不知道和上面简单的一层神经网络有没有关系）。

隐藏层（hidden layer）

对于隐藏层（hidden layer），我们同样使用chainrule，得到

其中，a_k是与a_j相连接的所有下一层结点，所以ａ_k可以表示成上一层的线性组合，再通过一个activation函数，得到

然后把该公式带入上式，得到

根据该公式，我们可以发现，计算hidden层的delta需要先计算后一层的delta，delta的计算是从后面往前传递，所以称为backpropagation。

在计算得到所有的delat之后，我可以通过下式计算偏导数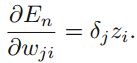：，如果结点是bias结点，z_i = 1，然后通过梯度下降求解参数w。

5.总结：

 

总的来说，训练神经网络的其实就是迭代地寻找到使得E(w)最小化的参数w，一般采用的是Gradient decent的方法，该方法有一个核心就是计算E(w)的梯度，而在神经网络中使用BP求解梯度，下面列出计算的流程：

1．  给定一个输入向量x，通过forward propagation计算所以hidden结点和output结点的activation。

2．  计算output结点的delta。

3．  根据output结点的delta，通过back propagation计算所有hidden结点的delat。

4．  然后通过计算想要的偏导数。

 

需要注意的是，我们上面是以on-line为列介绍神经网络的BP，如果是batch方法也是类似的，只是在整个数据集上重复上面的过程，然后把偏导数求个和得到。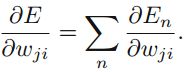

整个神经网络的流程就是训练w，流程如下：

(1)初始化一个参数w；

(2)按当前的w值，用BP计算E(w)的梯度；

(3)按Gradient decent公式更新，得到一个新的参数w；

(4)反复(2)和(3)，直到w收敛。

6.Reference：

《Pattern Recognition and Machine Learning》ChristopherM. Bishop

《Pattern Recognition and Machine Learning》读书笔记

UFLDL Tutorial  http://deeplearning.stanford.edu/wiki/index.php/UFLDL_Tutorial