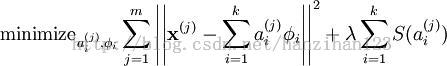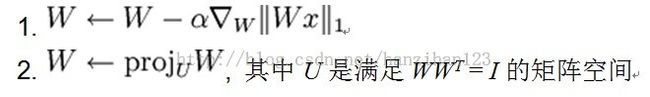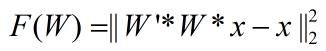Deep Learning 系列（4）：稀疏编码（sparse coding）和主成分分析（ICA）

一直犹豫稀疏编码怎么写，来来回回看了好几遍的UFLDL。因为这不仅是DL深度学习的重要概念，也是我这段时间一直在研究的stacked ISA 深度特征学习的支柱。

这章将主要介绍一下稀疏编码的主要概念，及主成分分析的方法。

一. 稀疏编码（sparse coding）：

稀疏编码算法是一种无监督（unsupervised）学习方法，它用来寻找一组“超完备”基向量来更高效地表示样本数据。（设x的维数为n，则k>n）

超完备基能更有效地找出隐含在输入数据内部的结构与模式。然而，系数a不再由x唯一确定，则，加入“稀疏性”来解决超完备而导致的退化问题。

如：

 

 

“稀疏性”为只有很少的几个非零元素或只有很少的几个远大于0的元素。

这里将m个输入向量的稀疏编码代价函数定义为：

其中，S（.）是稀疏代价函数，对远大于0的a进行“惩罚”。通常选择范式代价函数S(a)=|a|及对数代价函数S(a)=log(1+a^2).  通常，为了防止减少a或增加φ，使稀疏惩罚变小，将限制||φ||^2小于常量C。

 

学习基向量集的方法由1.逐个使用训练样本x来优化系数a，2.一次性处理多个样本来对基向量Φ进行优化。

局限性：即使已经学习得到一组基向量，如果要对新的数据样本进行“编码”，必须再次执行优化过程来得到所需的系数，计算成本增加。

二、 主成分分析（ICA）

 

稀疏编码得到的基向量之间不一定线性独立。独立主成分分析（ICA）学习的基不仅线性独立，而且还标准正交（ΦΦ^T=I）

这里，ICA主要学习一组基向量W，通过W将x映射到特征，特征是稀疏的。（与sparse coding相反）。

标准正交ICA的目标函数是：（两种表达）

 Minimize   J(W)=|(|Wx|)|

      s.t. WW’=I

约束WW’=I 隐含另外两个约束：

1.     基向量的个数须小于输入数据的维度（非超完备），因为要学习一组标准正交基

2.     数据必须无正则ZCA白化。（正则化  值得看！） 

优化目标函数，可以使用梯度下降法，并在每一步增加投影步骤： 

 

然而，在UFLDL的教程Deriving gradientsusing the backpropagation idea 中重建了代价函数为：

套用 BP反向传播求导：（回想UFLDL之反向传导）

求偏导公式：

W的正交性公式为：

关于实现代码，可以参见tornadomeet的博客之ICA模型练习。（有改动）

之后，也会上传相关代码。

 

参考：

1. tornadomeet的博客

2. dark的博客

3. 搜不狐 （正则化和归一化）

4. UFLDL 教程

5. 关于ICA，的文章Natural Image Statistics（Aapo Hyv¨arinen），很长，很经典，值得看！

持续更新中。。。。（PS：CSDN的编辑功能是不是应该升级了呀！不能编辑公式，也不能复制，相当麻烦！）