Cracking the Coding Interview:: 寻找有环链表的环路起始节点

给定一个有环链表，实现一个算法返回环路的开头节点。 这个问题是由经典面试题-检测链表是否存在环路演变而来。这个问题也是编程之美的判断两个链表是否相交的扩展问题。

首先回顾一下编程之美的问题。 由于如果两个链表如果相交，那么交点之后node都是共享（地址相同）的，因此最简单暴力的方法就是两个for循环，判断该链表的node是否属于另外一个链表。但是这个算法复杂度是O(length1 * length2)。如果链表较长，这个复杂度有点高了。

当然也可以遍历其中某个链表，将node的地址存储hash table中；然后接下来遍历另外一个链表，查找node是否在这个hash table中。这样的话时间复杂度就是O(length1 + length2)。但是需要额外的O(length1)的空间。在C++ STL Java等主流语言中，hash table都有很好的实现，因此编程也比较简单。

注意我们这个方法是认定如果两个链表相交，那么肯定交点以后的点都是共享的，包括最后一个点。那么找到链表的最后一个节点，如果节点相同，那么就相交。当然了，以上算法需要处理有环存在的情况。

本文的问题是寻找有环链表的开头节点，那么如何判断一个链表是否有环？

我们可以用快慢游标的方法。具体来说，就是使用两个游标遍历链表，其中快游标（快指针，fastRunner）每次经过两个node，慢游标（慢指针，slowRunner）每次经过一个node。那么如果有环，那么这两个游标肯定会相遇。使用反证法可以推理这个推论是正确的，假如fastRunner正好经过了slowRunner，而没有相遇，那么上一部，就是fastRunner后退两步，slowRunner后退一步，两个runner必定相遇。如果现在slowRunner正好领先一步fastRunner，那么下一步二者相遇。

bool checkLinkRing(const Node *head)
{
  if( head == nullptr )
    return false;

  auto fastRunner = head;
  auto slowRunner = head;
  while( fastRunner->next != nullptr && fastRunner->next->next != nullptr )
  {
    fastRunner = fastRunner->next->next;
    slowRunner = slowRunner->next;
    if( fastRunner == slowRunner )
      return true;
  }

  return false;
}

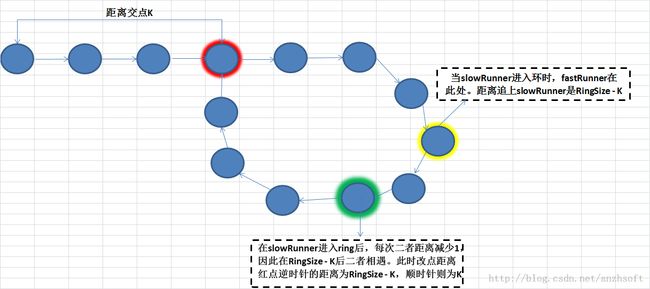
接下来的问题，如何找到环的起始点？看下图，假设交点在K处

那么在slowRunner走了K步到达交点，那么此时fastRunner走了2K步到达黄圈处。那么fastRunner距离追上slowRunner还有RingSize - K步。 注意，只能顺时针前进。fastRunner相对slowRunner的速度是每步经过一个node（fastRunner虽然每次经过2个node，但是slowRunner也向前走了一个node，因此每步二者的距离仅仅减少一个node），因此在走了RingSize - K时相遇。也就是slowRunner在进入环后，再走RingSize - K 步后二者相遇于绿处。此时，绿点顺时针距离交点有RingSize - ( RingSize - K) = K。注意括号内的RingSize - K是slowRunner走的。

关键问题出来了，在二者相遇的点，距离交点也是K： 与head到交点的距离相同。因此，我们可以调整两个游标，使slowRunnder从头开始，fastRunnder从相遇点开始，二者以相同的速度前行，必然在相交点再次相遇！

auto findRingCrossPoint(const Node *head) ->decltype(head)
{
  if( head == nullptr )
    return nullptr;

  auto fastRunner = head;// C++11, fastRunner is const Node *
  auto slowRunner = head;
  while( fastRunner->next != nullptr && fastRunner->next->next != nullptr )
  {
    fastRunner = fastRunner->next->next;
    slowRunner = slowRunner->next;
    if( fastRunner == slowRunner )
      break;
  }
  
  // in case that there is no ring.
  if( fastRunner != slowRunner )
    return nullptr;

  slowRunner = head;
  while( true )
  {
    fastRunner = fastRunner->next;
    slowRunner = slowRunner->next;
    if( fastRunner == slowRunner )
    {
      break;
    }
  }

  return fastRunner;
}