POJ 2352 STARS
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 12897 | Accepted: 5533 |
Description
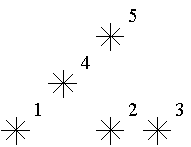
For example, look at the map shown on the figure above. Level of the star number 5 is equal to 3 (it's formed by three stars with a numbers 1, 2 and 4). And the levels of the stars numbered by 2 and 4 are 1. At this map there are only one star of the level 0, two stars of the level 1, one star of the level 2, and one star of the level 3.
You are to write a program that will count the amounts of the stars of each level on a given map.
Input
Output
Sample Input
5 1 1 5 1 7 1 3 3 5 5
Sample Output
1 2 1 1 0
Hint
Source
/*
http://acm.pku.edu.cn/JudgeOnline/problem?id=2352
线段树
线段树的空间设置为 4 * n 就够用了,因为按照这种建树的方法:
build(int l, int r)
{
if(l < r)
{
int mid = (l + r) / 2;
build(l, mid);
build(mid + 1, r);
}
}
树的深度最大为lg(n) + 2, 所以总的结点数最多为 (1 - 2 ^ (lng(n) + 2) / ( 1 - 2) = 4n - 1, 因此空间开4n足以应对
关于为什么深度最大为lg(n) + 2,画个图就明白了
*/
#include <iostream> #define MAX_N 130000 //线段树的容量 #define MAX_S 15005 //星星的最大数量 #define maxv(a, b) ((a) >= (b) ? (a) : (b)) #define minv(a, b) ((a) <= (b) ? (a) : (b)) using namespace std; //线段树结构 struct node { int l, r; //标识当前区段左右坐标的位置 int tsum; //total sum, 当前区域内权值的总和 int csum; // 当前区域被完全覆盖的次数 node() { tsum = csum = 0; } }nodes[MAX_N + 1]; int countv[MAX_S + 1]; int cord[MAX_S + 1][2]; //建树 void buildTree(int left, int right, int root) { nodes[root].l = left, nodes[root].r = right; if(left < right) { int mid = (left + right) / 2; //递归建立左子树 buildTree(left, mid, root * 2); //递归建立右子树 buildTree(mid + 1, right, root * 2 + 1); } } //为[left, right]区间每个元素增加1个值 void modify(int left, int right, int root) { nodes[root].tsum += (right - left + 1) * 1; if(nodes[root].l == left && nodes[root].r == right) nodes[root].csum += 1; else { int mid = (nodes[root].l + nodes[root].r) / 2; if(left <= mid) modify(left, minv(right, mid), root * 2); if(right >= mid + 1) modify(maxv(mid + 1, left), right, root * 2 + 1); } } //统计区间[left, right]内的总数值 int getVal(int left, int right, int root) { int res = 0; if(nodes[root].l == left && nodes[root].r == right) res += nodes[root].tsum; else { res += (right - left + 1) * nodes[root].csum; int mid = (nodes[root].l + nodes[root].r) / 2; if(left <= mid) res += getVal(left, minv(right, mid), root * 2); if(right >= mid + 1) res += getVal(maxv(mid + 1, left), right, root * 2 + 1); } return res; } int main() { int startNum, i, x, level; int maxX = INT_MIN; int minX = INT_MAX; cin>>startNum; for(i = 0; i < startNum; i++) { scanf("%d%d", &cord[i][0], &cord[i][1]); maxX = maxv(maxX, cord[i][0]); minX = minv(minX, cord[i][0]); } buildTree(minX, maxX, 1); for(i = 0; i < startNum; i++) { x = cord[i][0]; level = getVal(minX, x, 1); modify(x, x, 1); countv[level]++; } for(i = 0; i < startNum; i++) printf("%d/n", countv[i]); return 0; }