Some Shading Models in realtime rendering
前段时间有在这里(http://www.fseraph.com/?p=661)看到关于实时渲染中的一些常见渲染模型的总结,最近于是也找了些资料学习了一下,这里简单总结一下。
1. 一些基本概念
- Photon(光子): 波粒二象性;属于粒子;拥有波长;具有能量
- Radiant Energy(辐射能量): 光子集所具有的能量,
 ,单位:
,单位: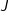 (焦耳)
(焦耳) - Radiant flux(辐射通量) , Radiant power(辐射功率):
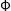 、
、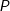 ,单位时间内的辐射能量
,单位时间内的辐射能量 (或光源在单位时间内所发射的光子所具有的能量),单位:
(或光源在单位时间内所发射的光子所具有的能量),单位: (瓦特,焦耳/秒)
(瓦特,焦耳/秒) - Flux density(通量密度), Irradiance(辐射照度):
 ,单位面积上的辐射通量
,单位面积上的辐射通量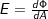 ,即:面积为
,即:面积为 的平表面上通过(进入或离开)的辐射通量;Irradiance则是特化后用来描述单位表面在其法向半球空间内进入该表面的辐射通量;单位:
的平表面上通过(进入或离开)的辐射通量;Irradiance则是特化后用来描述单位表面在其法向半球空间内进入该表面的辐射通量;单位: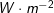
- Radiant intensity(辐射强度):
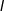 ,单位实体角上的辐射通量
,单位实体角上的辐射通量 ,即:在某个方向上通过(进入,发射或穿过)某一点的辐射通量;Solid angle(实体角):三维空间中的二维角度;在球面度上进行衡量;
,即:在某个方向上通过(进入,发射或穿过)某一点的辐射通量;Solid angle(实体角):三维空间中的二维角度;在球面度上进行衡量;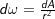 :在半径为
:在半径为 的空间球上,实体角
的空间球上,实体角 所对应的区域的球面表面积为
所对应的区域的球面表面积为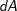 ;单位:
;单位:
- Radiance(辐射亮度):
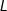 ,单位实体角、单位投影面积的表面元素上在某一方向
,单位实体角、单位投影面积的表面元素上在某一方向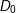 上通过(进入、发射或穿过)的辐射通量
上通过(进入、发射或穿过)的辐射通量 (
(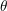 为方向
为方向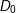 与表面法向之间的夹角);比如,在各个方向上相同的辐射亮度对应着与
与表面法向之间的夹角);比如,在各个方向上相同的辐射亮度对应着与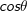 成比例的辐射强度;在某一点上的辐射亮度与距离无关;单位:
成比例的辐射强度;在某一点上的辐射亮度与距离无关;单位: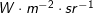
2. Bidirectional Reflectance Distribution function
BRDF(双向反射分布函数)用来描述物体表面入射与反射光线之间的关系,其数学形式上的表示:在物体表面上的点![]() 处,出射方向
处,出射方向![]() 上所反射的辐射亮度的微分与入射方向
上所反射的辐射亮度的微分与入射方向![]() 所进入的辐射照度的微分之间的比率;因而,BRDF是一个关于
所进入的辐射照度的微分之间的比率;因而,BRDF是一个关于![]() 的三元函数,量化公式为:
的三元函数,量化公式为:
将上式变型后即可以得到在![]() 点处的反射方程:
点处的反射方程:
该积分式计算出了物体表面在一定光源条件下特定方向上的辐射亮度,于是也就最终决定了其被人眼感知时所得到的形象。其中的核心就是BRDF所涉及的部分,它也是特化出不同渲染模型所对应的变化关键。
BRDF的一些属性。首先是一些基本的公共属性:
- Wavelength dependency, 波长相关:不同波长的光线在其表面上应有不同的反射结果,因而其是波长相关的。
- Reciprocity, 互反性:变换入射和出射光线的方向并不会影响BRDF的值,数学上的描述为:
。这个属性在一些基于物理的渲染中很重要,比如Bidirectional path tracing等(但在实时渲染模型中可能会被忽略)。
- Energy conservation, 能量守恒: BRDF需要满足能量守恒定律,即要求从一表面点上反射出的总能量不大于进入该点的总能量。对于一表面点
 进行量化后有:
进行量化后有:。大多数BRDF都能一定程度上满足此属性,这样会让渲染结果看起来更自然;但在严格意义上地满足该约束则不太容易,它要求能量不能被无缘由地损失或减少(这些在基于物理的渲染中可能很重要)。
- Anisotropy & Isotropy, 各向异性&各向同性:如果BRDF是关于表面法向量是旋转对称的,它的结果只取决于
 以及所对应的方位角
以及所对应的方位角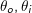 之间的差值
之间的差值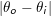 ,那么其为各向同性的;反之则其为各向异性。大多数金属质感材质的BRDF具有各向差异的属性。
,那么其为各向同性的;反之则其为各向异性。大多数金属质感材质的BRDF具有各向差异的属性。
- 直观简单的参数化:BRDF需要若干关键参数来进行调制,直观易用的参数能使美工更方便地对材质的各项属性进行设置,极大地降低使用难度以及提高使用效率。
- 更高的计算效率: 效率是实时渲染中最主要的考虑因素,这也正是各种高效Phong模型很流行,其它有更好表现力的模型并不被广泛使用的重要原因之一。关于BRDF的计算效率包括两方面,即时间和空间;在当前的GPU架构下一般来说对于每个Pixel均需要进行对应的BRDF计算,因而这两个方面的效率同样重要。
3. 菲涅尔反射(Fresnel Reflectance)
当然,在BRDF之中由于只考虑光线的双向反射分布,因而可以只取其中的
- 高近似度的还原需要的计算量过大;
- 几近真实的物理属性参数并不尽可知;
其中的
4. 一些常见的渲染模型
对反射方程的原始积分式直接计算显然不太可行,需要采用离散化的方式进行简化,这里通常结合对于光源的狄拉克脉冲函数建模的方法进行(看这里); 简化后可得:
![]()
这样,对于有限个方向上的光源进行叠加即可得到最终的渲染结果;在分析过程中只需要考虑一个方向上的光线影响,即有:
![]()
转换为另外一种抽象表达的形式以便于后述对于各种渲染模型的分析(注意:此处的I 并非前述的辐射强度):
![]()
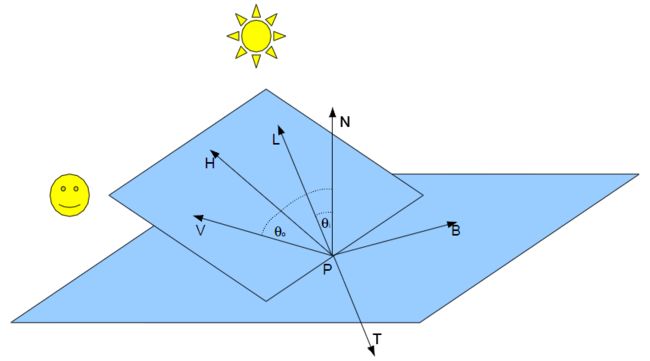
上式中的![]() 为物体表面的法向量,
为物体表面的法向量,![]() 为光线到表面点的向量,而V则为视点到表面点的向量;其中的
为光线到表面点的向量,而V则为视点到表面点的向量;其中的![]() 表示两个单位向量之间的点乘,用来取代
表示两个单位向量之间的点乘,用来取代![]() 分量;原始
分量;原始![]() 的三个参数此时也完全可以由
的三个参数此时也完全可以由![]() 来直接、间接地转换并替代(见下图示):
来直接、间接地转换并替代(见下图示):
通常来说BRDF是关于表面多种属性的反射结果之间的线性组合(在实时渲染中一般只考虑diffuse和specular两种即可),其可以量化表示为:
![]()
其中的![]() 分别表示两种反射的结果,
分别表示两种反射的结果,![]() 表示其对应的权重;如此一来通过调制组合中的四个参数就可以得到不同渲染表现的BRDF。接下来看一下一些常见的模型:
表示其对应的权重;如此一来通过调制组合中的四个参数就可以得到不同渲染表现的BRDF。接下来看一下一些常见的模型:
Lambert
Lambert模型是最简单的一种形式,它主要是用来还原完全的diffuse reflection效果(入射的光线在称为Lambert 的表面上均匀地反射向外部的各个方向),而不考虑specular反射;其BRDF的表述为:而在实时渲染中又通常将上式中的![]() 直接替换为diffuse颜色值
直接替换为diffuse颜色值![]() ,因而其最终的BRDF调制因数就为:
,因而其最终的BRDF调制因数就为:
![]()
单纯的兰伯特模型使用较少,它通常是被合理地融入到其它更复杂的模型之中。
Phong
Phong应该说是当前使用得最多的一种渲染模型,它在diffuse反射的基本上加入了glossy specular反射,其关于该部分的计算使用了光线从表面射出的方向
上式中的![]() 即为glossy specular反射分量:其中的
即为glossy specular反射分量:其中的![]() 为对应的specular color(与
为对应的specular color(与![]() 类似);
类似);![]() 部分可以用来约去反射方程中外部的几何因子;调节其中的
部分可以用来约去反射方程中外部的几何因子;调节其中的![]() 可以控制高光区域的范围:较大的
可以控制高光区域的范围:较大的![]() 对应较小范围的高光区域,反之则相对;关于
对应较小范围的高光区域,反之则相对;关于![]() 的计算为:
的计算为:![]() 。
。
基本Phong模型的BRDF调制因数为:
一般情况下有![]() ,但也可以使其值小于1,只要不大于1其均满足energy consveration的约束。
,但也可以使其值小于1,只要不大于1其均满足energy consveration的约束。
- Blinn-Phong
Blinn-Phong是在原始Phong基础上对计算细节做了改动,其使用halfway vector:
来计算specular反射分量的值:
其与原始Phong在计算效率上还是有所差别:当某些情况下
恒定不变时,可以预计算出
统一使用,因其不依赖于表面法向量
(依赖
则要求在每个Pixel均需计算);其它情况下,计算R则更加节省(至少可以节省出开方操作)。B-P的调制参数为(其余的
均无变化):
- Modified-Phong
P和B-P两种模型中的
中均有关于
的除法操作,这样就会在
(也即光线与法线几近垂直时)处产生数学运算上的问题进而导到BRDF的互反性(Reciprocity)不被满足。在Modified-Phong中就直接去掉了这一操作来避免这个问题,其BRDF如下:
因而这种修改也被称为:reciprocal (Blinn-)Phong。虽然这个简单的修改可以避免0除问题,但同时也会使得在
的周围的渲染效果看起来不太自然。此处的BRDF有:
- Max-Phong
另一种关于基本Phong的变型是Max-Phong,其相对于前几种可以在一定程度上更好地模拟具有光滑金属质感的表面,同时也使用了Modified-Phong的方法来保持BRDF的互反性,其BRDF如下所示:
此时有:
前述几种Phong模型都是实时渲染中最为常用的反射模型,其公共特点是参数都比较容易调节、计算效率也比较高,这也正是其流行的主要原因;它们之间的主要区别均在于其对![]() 部分使用的不同计算方法,但是总体来说Phong模型对于
部分使用的不同计算方法,但是总体来说Phong模型对于![]() 部分的表现力度还是不够,而这也是其它更加复杂的渲染模型所改进的重点之一。
部分的表现力度还是不够,而这也是其它更加复杂的渲染模型所改进的重点之一。
Oren-Nayar
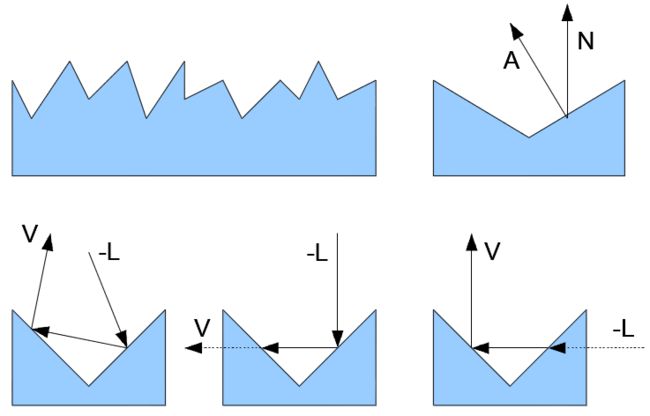
Lambert方法是一种基本的漫射模型,它假定光线在物体的表面朝各个方向上均匀发散,而这显然不太符合物理事实,特别是对于一些表面较为粗糙的材质;Oren-Nayar模型是另外一种基于一定物理事实的漫射模型,它能更好地反映这类材质表面的漫射现象。该模型的分析基于微表面方法,该方法主要建立在以下几个假设的基础上(图示如下):- 物体的表面是由一些微小得对称的V形结构组成;微表面之间有相互反射
- 每个V表面的宽度要远远小于其长度
- 每个微表面的面积要远远大于光线的波长(这点很容易满足)
- 每个Pixel要能够覆盖足够多的微表面
- 每个微表面具有Lambert漫射属性
![]()
其中的![]() 表示
表示![]() 两个向量在
两个向量在![]() 点处的切平面上的投影向量之间的夹角;另有:
点处的切平面上的投影向量之间的夹角;另有:
上式中的![]() 表示材质表面的粗糙度,有效取值范围为
表示材质表面的粗糙度,有效取值范围为![]() ;其值越大则漫射方向的分布越不均匀,当其为0时对应漫射方向的均匀分布,此时退化为Lambert模型。对该模型的BRDF用另外一种形式表述后有:
;其值越大则漫射方向的分布越不均匀,当其为0时对应漫射方向的均匀分布,此时退化为Lambert模型。对该模型的BRDF用另外一种形式表述后有:
![]()
而其中![]() 对应
对应![]() 在
在![]() 点的切平面上的单位投影向量,这样就可以得到其BRDF调制参数:
点的切平面上的单位投影向量,这样就可以得到其BRDF调制参数:
Oren-Nayar相对于Lambert来说对于diffuse反射有更强的表现力,不过其代价就是不菲的计算量,这之中主要涉及:
- 对于
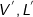 的计算:这个操作对于每个Pixel均要进行,因其与N相关。
的计算:这个操作对于每个Pixel均要进行,因其与N相关。 - 对于
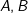 分量的计算:若物体表面使用统一的
分量的计算:若物体表面使用统一的 则可以预计算后直接使用;若物体表面使用不统一的
则可以预计算后直接使用;若物体表面使用不统一的 ,则需要动态计算
,则需要动态计算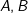 (通常将该信息存储到纹理,这样就有额外的纹理读取开销)。
(通常将该信息存储到纹理,这样就有额外的纹理读取开销)。
Cook-Torrance
其中
Ashikhmin-Shirley
Ashikhmin-Shirley是一种各向异性模型,其BRDF如下:其中:
上述式子中的
Ward
Ward同样是一种各向异性的模型,它在一定程度上也是依赖于微表面理论作为依据,但并不严格,不过其最终还是获得了不错的效果;同时该模型也满足能量守恒和互反性。各向异性的Ward模型的BRDF表述如下:其中的