【工程数学】若干种插值算法

// ConsoleAppLagrangeSolu.cpp : 定义控制台应用程序的入口点。
//
/* 
*函数功能：拉格朗日插值法，数据拟合基础 
*函数原形：double LagrangeSolu(int N,vector<double> &X,vector<double> &Y,double x)
*参数：int N,vector<double> &X,vector<double> &Y,double x
*int N：插值次数
*vector<double> &X：存储插值节点的各个递增值xi
*vector<double> &Y：存储插值节点xi对应的值yi
*double x：待估计的节点
*返回值：通过x这个节点值计算估计函数对应的y值 
*时间复杂度：O(n^2) 
*备注： 本程序尽是在原作者基础上的简单改动与深刻理解
*日期：2014/12/15 
*原创：否 ,原作者:xiaowei_cqu
*作者：<span style="font-family: Arial, Helvetica, sans-serif;">xiaowei_cqu</span>
*Email：<span style="font-family: Arial, Helvetica, sans-serif;">http://blog.csdn.net/xiaowei_cqu</span>
 
*/ 
#include "stdafx.h"
#include <iostream>    
#include <vector>  

using namespace std;  

void LagrangeTest();
double LagrangeSolu(int N, vector<double> &X, vector<double> &Y,double x);  

int _tmain(int argc, _TCHAR* argv[])
{  
	LagrangeTest();
	return EXIT_SUCCESS;  
}  

double LagrangeSolu(int N,vector<double> &X,vector<double> &Y,double x)
{  
	double result=0;  
	for(int i=0;i<N;i++)
	{  
		double temp=Y[i];  
		for(int j=0;j<N;j++)
		{  
			if(i!=j)
			{  
				temp = temp*(x-X[j]);  
				temp = temp/(X[i]-X[j]);  
			}  
		}  
		result += temp;  
	}  
	return result;  
}

void LagrangeTest()
{
	char a='n'; 
	do{  
		int N;
		cout<<"请输入差值次数n的值："<<endl;    
		cin>>N;  

		vector<double>X(N,0);//具有n个int类型元素，且值均为0的vecotr容器X,Y  
		vector<double>Y(N,0); //X存储的是将要插值的递增节点，Y是其对应的函数值
		cout<<"请输入插值点对应的值及函数值(Xi,Yi)："<<endl;  
		for(int i=0;i<N;i++)
		{  
			cin>>X[i]>>Y[i];  
		}  

		double x;
		cout<<"请输入要估计的值x："<<endl;  
		cin>>x;  

		double result=LagrangeSolu(N,X,Y,x);  
		cout<<"由拉格朗日插值法得出结果： "<<result<<endl;  
		cout<<"是否要继续？(y/n)：";  
		cin>>a;  
	}while(a=='y');
}

// ConsoleAppNewtonInterpolationSolu.cpp : 定义控制台应用程序的入口点。
//
/* 
*函数功能：牛顿插值法
*函数原形：double  NewtonInSolu(vector<double> &X,vector<double> &Y,double x)
*参数：int N,vector<double> &X,vector<double> &Y,double x
*vector<double> &X：存储插值节点的各个递增值xi
*vector<double> &Y：存储插值节点xi对应的值yi
*double x：待估计的节点
*返回值：通过x这个节点值计算估计函数对应的y值 
*时间复杂度：O(n^2) 
*备注：
*日期：2014/12/19
*原创：否
*作者： xiaowei_cqu
*Bolg：http://blog.csdn.net/xiaowei_cqu
*/ 

#include "stdafx.h"
#include <iostream>    
#include <vector>  

using namespace std;  

void NewtonInSoluTest();
double ChaShang(int n,vector<double>&X,vector<double>&Y);
double NewtonInSolu(vector<double> &X, vector<double> &Y,double x);  

int _tmain(int argc, _TCHAR* argv[])
{  
	NewtonInSoluTest();
	return EXIT_SUCCESS;  
}  

double NewtonInSolu(vector<double> &X,vector<double> &Y,double x)
{   
		double result=0;  
		for(int i=0;i<X.size();i++)
		{  
			double temp=1;  
			double f=ChaShang(i,X,Y);  //算差商
			for(int j=0;j<i;j++)
				temp = temp*(x-X[j]);  //求Wk（x）
			result += f*temp;  
		}  
		return result;   
}

double ChaShang(int n,vector<double>&X,vector<double>&Y)
{  
	double f=0;  
	double temp=0;  
	for(int i=0;i<=n;i++)
	{  
		temp=Y[i];  
		for(int j=0;j<=n;j++)  
			if(i!=j) 
				temp /= (X[i]-X[j]);  
		f += temp;  
	}  
	return f;  
} 

void NewtonInSoluTest()
{
	char a='n'; 
	do{  
		int N;
		cout<<"请输入差值次数n的值："<<endl;    
		cin>>N;  

		vector<double>X(N,0);//具有n个int类型元素，且值均为0的vecotr容器X,Y，这两个量是vector<double>的对象  
		vector<double>Y(N,0); //X存储的是将要插值的递增节点，Y是其对应的函数值,两者均是数组
		cout<<"请输入插值点对应的值及函数值(Xi,Yi)："<<endl;  
		for(int i=0;i<N;i++)
		{  
			cin>>X[i]>>Y[i];  
		}  

		double x;
		cout<<"请输入要估计的值x："<<endl;  
		cin>>x;  

		double result=NewtonInSolu(X,Y,x);  
		cout<<"由牛顿插值法得出结果： "<<result<<endl;  
		cout<<"是否要继续？(y/n)：";  
		cin>>a;  
	}while(a=='y');
}

结果与拉格朗日一样

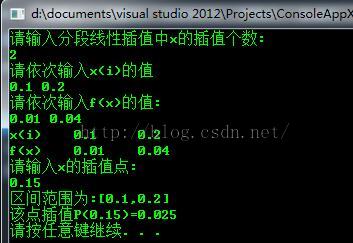
3，线性分段插值：

// ConsoleAppXianchazhi.cpp : 定义控制台应用程序的入口点。
//

#include "stdafx.h"

/****************************************************************************************\
*题目：分段线性插值 									*
*         		  		       					        *
\****************************************************************************************/
#include<iostream>
#define MAX 100
using namespace std;
int main()
{
	system("color 0A");
	int MAX_SIZE,i,j;
	double x[MAX],f[MAX];
	//输入部分
	cout<<"请输入分段线性插值中x的插值个数:"<<endl;
	cin>>MAX_SIZE;
	cout<<"请依次输入x(i)的值"<<endl;
	for(i=1;i<MAX_SIZE+1;i++)
	{
		cin>>x[i];
	}
	cout<<"请依次输入f(x)的值:"<<endl;
	for(i=1;i<MAX_SIZE+1;i++)
	{
		cin>>f[i];
	}
	//输出部分
	cout<<"x(i)";
	for(i=1;i<MAX_SIZE+1;i++)
		cout<<"\t"<<x[i];
	cout<<endl;	
	cout<<"f(x)";
	for(i=1;i<MAX_SIZE+1;i++)
		cout<<"\t"<<f[i];
	cout<<endl;
	//计算部分
	//确定(x1,x2)区间
	double n,p;
	cout<<"请输入x的插值点:"<<endl;
	cin>>n;
	double def=0;
	for(i=1;i<MAX_SIZE+1;i++)
	{
		def=x[i]-n;
		if (def>0) 
		{
			j=i;
			break;
		}
	}
	cout<<"区间范围为:["<<x[j-1]<<","<<x[j]<<"]"<<endl;
	//计算插值点数值
	p=((n-x[j])/(x[j-1]-x[j]))*f[j-1]+((n-x[j-1])/(x[j]-x[j-1]))*f[j];
	cout<<"该点插值P("<<n<<")="<<p<<endl;
	system("pause");
	return 1;
}