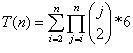《编程之美》笔记之——24点游戏
原著中给出了两种解法:穷举和分治。后来加上去除冗余括号等操作,自己写了四个实现代码,但完全还是用的原著中的算法思想。暂且把自己的实现过程记录下来。
自己的第一种代码实现,完全穷举,没有任何的优化。代码写得极其笨拙。程序穷举了四个数字能组成的所有可能的算式,分别计算它们的值,找到结果是24的那个算式,输出它。一个不带括号的算式总是有形式a op1 b op2 c op3 d,其中a,b,c,d是运算数,op1,op2,op3是运算符。代码中一个三重循环穷举三个运算符的43种组合,然后在每种组合下再穷举四个运算数的所有4!种排列,这样便得到了一个没有括号的算式。然后穷举五种加括号的形式,逐个判断值是否为24。这个过程中唯一值得回忆和感兴趣的是四个运算数五种不同加括号方式的由来。这是一个经典的Catalan数问题。
这个经典Catalan数问题在组合数学教材上都能找到。原题目是:n 个数相乘, 不改变它们的位置, 只用括号表示不同的相乘顺序,令g(n)表示这种条件下构成不同乘积的方法数,令C(n)表示第n个Catalan数。则有g(n)=C(n-1)。前几个Catalan数为:C(0)=1,C(1)=1,C(2)=2,C(3)=5,C(4)=14,C(5)=42。所以g(4)=C(3)=5。根据Catalan数的计算公式,有g(4)=g(1)g(3)+g(2)g(2)+g(3)g(1)。Catalan数的计算公式也同时提供了构造答案的方法。对于4个数,中间有3个位置,可以在任何一个位置一分为二,被分开的两半各自的加括号方案再拼凑起来就得到一种4个数的加括号方案:
只有一个数时:(A),一种
两个数:g(2)=g(1)g(1),所以是(A)(B)=(AB),一种
三个数:g(3)=g(1)g(2)+g(2)g(1)=(A)(BC)+(AB)(C),两种
四个数:g(4)=g(1)g(3)+g(2)g(2)+g(3)g(1)
=(A)[(B)(CD)+(BC)(D)]+(AB)(CD)+[(A)(BC)+(AB)(C)](D)
=A(B(CD)) + A((BC)D) + (AB)(CD) + (A(BC))D + ((AB)C)D
共有五种。于是写代码枚举这五种加括号的方式即可。这种方法只是一种能得到正确答案的方法,扩展性和效率都极差。而且生成的表达式中也有冗余括号。
同样是这种思想,《编程之美》上给出了一种优化的实现方法。一个算术表达式,无论如何复杂,总是按照优先级取出两个运算数进行运算得到一个中间结果,把这个中间结果加入到原表达式中,不断重复这一过程,直到剩下一个数。根据这个思想,可以很快写出实现代码。《编程之美》上即给出了一个完整的代码。
第二种实现的效率和扩展性显然不是第一种能比的。把两个数之间的一次加、减、乘、除看作一次基本运算。那么第一种实现要穷举四种运算符可重复的3组合,有43种,然后4个运算数的全排列,有4!种,之后5种不同的加括号方案,第种括号下要进行3次运算。总共需要做:43*4!*5*3=23040次基本运算。在第二种实现中,假设T(n)表示n个数要进行的基本运算次数,则T(1)=0, T(2) = 6, T(n)=C(n,2)*[6 + 6*T(n-1)]。其中C(n,2)表示n个数中取2个数的组合数。在第二种实现中,对于每一个2-组合,都要做6次基本运算,然后得到6个n-1个数的子问题。所以有上述公式。根据T(n)的公式,T(3)=126, T(4)=4572,所以在第二种实现方法中,穷举4个数的24点问题最多需要做4572次基本运算,这远低于第一种实现的23040次。
第二种实现所需要穷举的基本运算次数公式T(n)写成下面的形式更好看:
例如T(4)=C(4,2)*6+C(4,2)*6*C(3,2)*6+C(4,2)*6*C(3,2)*6*C(2,2)*6,这个形式让人感觉更有规律。那么有个问题:T(n)的最小值是多少?第二种实现有没有冗余计算?对于冗余计算,我觉得应该说,第二种实现可能会产生重复的计算,在4个运算数有重复的时候便会如此,但应该不会重复计算本质上相同的表达式。比如在第一种实现中,当三个运算符都是加的时候,四个数的全排列以及每种全排列下的五种加括号方案所形成的120个表达式都是本质上相同的。
效率的问题由于能力的限制只能止于此了。下面是另一个问题:去除冗余括号。对于去除冗余括号,自己写了两个不同的实现代码。还是像上面一样,不管这个实现的效率有多低,代码有多笨拙,自己只是想验证一下这种想法可以得到正确答案。
自己的第一个去除冗余括号的方法是:先把得到的中缀表达式转化为后缀表达式,这样可以把所有括号都去掉,然后把后缀表达式转化为中缀表达式,判断出必须加括号的情况,加上必要的括号。那么必须加括号的情况是什么呢?对于一个表达式树来说,当子表达式树的优先级严格低于根的优先级时,应该用括号把子表达式保护起来。另外,当根的运算是减号时,右子树为加号或减号的话则应该用括号保护,当根的运算是除法时,右子树如果是乘法或者优先级低于除法的应该保护。初始时运算数的优先级高于所有的优先级,这样可以避免给运算数加上冗余的括号。其实现代码附在最后。
第二个去除冗余括号的方法是:并不是在最后得到结果后才开始统一去除冗余括号,而是在每一步计算中都判断是否应该把子表达式加括号保护。这种方法更简单,效率更高。把《编程之美》原书中解法一的实现代码略做修改即可。完整的实现代码附在最后。
《编程之美》上给出的最后一个解法是用分治的思想。在原著中这个方法讲得非常详细。用一个公式来说就是f(A)=UFork(f(A1), f(A-A1)),其中A1取遍A的所有非空真子集,U表示求集合的并集,f(A)表示集合A中元素进行所有可能的四则混合运算所得到的值(不存在重复)。Fork(A,B)定义为:Fork(A,B)={a+b,a-b,b-a,a*b,a/b(b!=0),b/a(a!=0) | a 属于集合A,b属于集合B}。这个解法另一个值得学习的地方就是代码实现的技巧,从低位起第i个二进制位为1表示第i个数在这个集合中。下面是自己参照《编程之美》最后这种分治法的伪代码写的实现代码:
struct Node { string exp; double value; Node() { value = 0; } Node(const string& str, double v) { exp = str; value = v; } bool operator<(const Node& n) const { return value < n.value; } } cards[CardsNumber]; set<Node> S[1 << CardsNumber]; // f(i)的作用是求出i代表的那个集合中的所有元素进行四则运算的 // 结果,并将结果存放在S[i]中 void f(int i) { if(!S[i].empty()) return; for(int x = 1; x <= (i-x); x++) { if((x & i) == x) { // 找到一个真子集 f(x); //计算集合x,并将结果存放到S[x]中 f(i-x); //计算集合i-x,并将结果存放到S[i-x]中 set<Node>::iterator it1, it2; for(it1 = S[x].begin(); it1 != S[x].end(); it1++) { for(it2 = S[i-x].begin(); it2 != S[i-x].end(); it2++) { const Node& a = *it1, b = *it2; COUNT(); S[i].insert( Node("("+a.exp+"+"+b.exp+")", a.value+b.value)); COUNT(); S[i].insert( Node("("+a.exp+"-"+b.exp+")", a.value-b.value)); COUNT(); S[i].insert( Node("("+b.exp+"-"+a.exp+")", b.value-a.value)); COUNT(); S[i].insert( Node("("+a.exp+"*"+b.exp+")", a.value*b.value)); if(b.value != 0) { COUNT(); S[i].insert( Node("("+a.exp+"/"+b.exp+")", a.value/b.value)); } if(a.value != 0) { COUNT(); S[i].insert( Node("("+b.exp+"/"+a.exp+")", b.value/a.value)); } } } } } }
第二个实现代码(其中使用第二种去除冗余括号的方法):
int pre(const char& ch) { switch(ch) { case '(': case ')': return 0; case '+': case '-': return 1; case '*': case '/': return 2; } return 10; } int f(int n) { // n表示当前有几个数字 if(n == 1) { if(cards[0] == Dest) { cout << exp[0] << endl; return 1; } return 0; } int i, j; for(i = 0; i < n; i++) { for(j = i+1; j < n; j++) { R a = cards[i], b = cards[j]; cards[j] = cards[n-1]; string expa = exp[i], expb = exp[j]; exp[j] = exp[n-1]; int pa = prev[i], pb = prev[j], p; prev[j] = prev[n-1]; // + COUNT(); exp[i] = expa + "+" + expb; cards[i] = a + b; prev[i] = pre('+'); if(f(n-1)) return 1; // a-b COUNT(); exp[i] = expa + "-"; if(pb <= pre('-')) exp[i] += "(" + expb + ")"; else exp[i] += expb; cards[i] = a - b; prev[i] = pre('-'); if(f(n-1)) return 1; // b-a COUNT(); exp[i] = expb + "-"; if(pa <= pre('-')) exp[i] += "(" + expa + ")"; else exp[i] += expa; cards[i] = b - a; prev[i] = pre('-'); if(f(n-1)) return 1; // a*b COUNT(); p = pre('*'); if(pa < p) exp[i] = "(" + expa + ")" + "*"; else exp[i] = expa + "*"; if(pb < p) exp[i] += "(" + expb + ")"; else exp[i] += expb; cards[i] = a*b; prev[i] = p; if(f(n-1)) return 1; // a/b if(b.numerator != 0) { COUNT(); p = pre('/'); if(pa < p) exp[i] = "(" + expa + ")" + "/"; else exp[i] = expa + "/"; if(pb <= p) exp[i] += "(" + expb + ")"; else exp[i] += expb; cards[i] = a/b; prev[i] = p; if(f(n-1)) return 1; } // b/a if(a.numerator != 0) { COUNT(); p = pre('/'); if(pb < p) exp[i] = "(" + expb + ")" + "/"; else exp[i] = expb + "/"; if(pa <= p) exp[i] += "(" + expa + ")"; else exp[i] += expa; cards[i] = b / a; prev[i] = p; if(f(n-1)) return 1; } exp[i] = expa; exp[j] = expb; cards[i] = a; cards[j] = b; prev[i] = pa; prev[j] = pb; } } return 0; }
其中R是自己定义的一个分数类。
上面的代码都只是为了得到结果。其中COUNT()宏是用来统计得到结果所用的基本运算次数。在分治法的实现中,因为集合中不允许有重复元素,所以insert操作不一定总成功,但即使不成功,也进行过一次基本运算,所以计入了总数。自己写程序把以上几种实现代码的输出结果组织成了一个HTML表格,用来对比,如下:
| Cards | Expression 1 | Count 1 | Expression 2 | Count 2 | Expression 3 | Count 3 |
| 5 5 5 1 | (5-(1/5))*5 | 10872 | (5-1/5)*5 | 2057 | (5*(5-(1/5))) | 1253 |
| 3 3 7 7 | (3+(3/7))*7 | 5052 | (3/7+3)*7 | 1216 | (7*(3+(3/7))) | 1844 |
| 3 3 8 8 | 8/(3-(8/3)) | 19998 | 8/(3-8/3) | 1359 | (8/(3-(8/3))) | 1820 |
| 4 4 10 10 | ((10*10)-4)/4 | 14295 | (10*10-4)/4 | 4138 | (((10*10)-4)/4) | 1784 |
| 1 4 5 6 | 4/(1-(5/6)) | 19893 | 6/(5/4-1) | 2930 | (6/((5/4)-1)) | 2122 |
| 3 8 8 10 | ((8*10)-8)/3 | 14220 | (8*10-8)/3 | 3468 | (((8*10)-8)/3) | 2282 |
| 9 9 6 2 | (9+(9-6))*2 | 2172 | (9+9-6)*2 | 55 | (9*((6/9)+2)) | 2180 |
| 12 5 10 11 | Unsolvable | 23040 | Unsolvable | 4572 | Unsolvable | 2736 |
| 3 7 6 5 | (7+(6-5))*3 | 2307 | (7+5)/(3/6) | 1362 | (3*(7-(5-6))) | 2706 |
| 12 9 3 5 | 12+((9-5)*3) | 2181 | (12-9+5)*3 | 133 | (12-(3*(5-9))) | 2681 |
| 10 9 9 4 | 10+(9+(9-4)) | 363 | 10+9-4+9 | 10 | (10-((4-9)-9)) | 2240 |
| 7 12 8 12 | 12+((8-7)*12) | 2286 | 12-(7-8)*12 | 913 | (12-((7-8)*12)) | 2252 |
| 9 4 7 5 | 9+((7-4)*5) | 2196 | 9*4-5-7 | 389 | (9-((4-7)*5)) | 2687 |
| 4 8 12 8 | 8+(12+(8-4)) | 498 | 12-(4-8-8) | 137 | ((8+(12+8))-4) | 2100 |
| 10 2 1 7 | 10+(2*(1*7)) | 3603 | 10*1+2*7 | 1251 | (10+(2/(1/7))) | 2274 |
| 12 4 10 9 | 12*(10/(9-4)) | 16248 | 12*10/(9-4) | 1248 | (12/((9-4)/10)) | 2718 |
| 4 7 12 9 | 7+(12+(9-4)) | 498 | (4+7-9)*12 | 13 | (4/((9-7)/12)) | 2742 |
| 8 9 9 13 | Unsolvable | 23040 | Unsolvable | 4512 | Unsolvable | 2234 |
| 10 11 10 6 | Unsolvable | 23040 | Unsolvable | 4512 | Unsolvable | 2282 |
| 6 4 5 7 | (5+(7-6))*4 | 2412 | (6-4)*(7+5) | 217 | (4*((5+7)-6)) | 2682 |
| 10 7 8 2 | Unsolvable | 23040 | Unsolvable | 4564 | Unsolvable | 2651 |
| 5 5 2 2 | (5+(5+2))*2 | 732 | (5+5+2)*2 | 6 | ((5*5)-(2/2)) | 1677 |
| 11 12 10 4 | 11+(10+(12/4)) | 1113 | 11+10+12/4 | 877 | (11+(10+(12/4))) | 2724 |
| 4 4 5 5 | (5+(5-4))*4 | 2412 | 5*5-4/4 | 560 | (4*((5+5)-4)) | 1712 |
| 6 10 11 6 | Unsolvable | 23040 | Unsolvable | 4512 | Unsolvable | 2324 |
| 7 9 10 10 | Unsolvable | 23040 | Unsolvable | 4512 | Unsolvable | 2282 |
| 2 6 2 12 | (2+2)*(12-6) | 3294 | (6-2)*12/2 | 282 | (2*(6+(12/2))) | 1926 |
| Ave:9810 | Ave:1844 | Ave:2256 |