二路归并排序算法(递归&非递归)
归并(Merge)排序法是将两个(或两个以上)有序表合并成一个新的有序表,即把待排序序列分为若干个子序列,每个子序列是有序的,然后再把有序子序列合并为整体有序序列。
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。
时间复杂度为O(nlogn),空间复杂度为 O(n),归并排序比较占用内存,但却效率高且是稳定的算法。
以下为递归实现的版本:
#include<iostream>
using namespace std;
void Merge(int arr[],int low,int mid,int high)
{//low为第1有序区的第1个元素,i指向第1个元素, mid为第1有序区的最后1个元素
int i=low,j=mid+1,k=0; //mid+1为第2有序区第1个元素,j指向第1个元素
int *temp=new(nothrow) int[high-low+1]; //temp数组暂存合并的有序序列
if(!temp)//内存分配失败
{
cout<<"ERROR!";
return;
}
while(i<=mid && j<=high)//顺序选取两个有序区的较小元素,存储到t数组中
{
if(arr[i]<=arr[j])//较小的先存入temp中
temp[k++]=arr[i++];
else
temp[k++]=arr[j++];
}
while(i<=mid)//若比较完之后,第一个有序区仍有剩余,则直接复制到t数组中
temp[k++]=arr[i++];
while(j<=high)//同上
temp[k++]=arr[j++];
for(i=low,k=0;i<=high;i++,k++)//将排好序的存回arr中low到high这区间
arr[i]=temp[k];
delete []temp;//删除指针,由于指向的是数组,必须用delete []
}
void MergeSort(int arr[],int low,int high)
{//用递归应用二路归并函数实现排序——分治法
if(low<high)//(是if,不是while!,且不含等号!否则死循环!)
{
int mid=(low+high)/2;
MergeSort(arr,low,mid);
MergeSort(arr,mid+1,high);
Merge(arr,low,mid,high);
}
}
int main()
{
int x[]={0,5,-2,1,-8,7,6,-3};
MergeSort(x,0,7);
for(int i=0;i<8;i++)
cout<<x[i]<<" ";
return 0;
}
参考 http://www.cnblogs.com/hackerain/archive/2011/01/07/2130424.html
非递归实现版本:
Merge函数和上面递归实现是完全一样的,MergeSort形参改成了待排序数组和数组大小。
#include<iostream>
using namespace std;
void Merge(int arr[],int low,int mid,int high)//递归和非递归均一样
{//将两个有序区归并为一个有序区
int i=low,j=mid+1,k=0;
int *temp=new(nothrow) int[high-low+1];
while(i<=mid&&j<=high)
{
if(arr[i]<=arr[j])
temp[k++]=arr[i++];
else
temp[k++]=arr[j++];
}
while(i<=mid) temp[k++]=arr[i++];
while(j<=high) temp[k++]=arr[j++];
for(i=low,k=0;i<=high;i++,k++)
arr[i]=temp[k];
delete []temp;
}
//void MergeSort(int arr[],int low,int high)//递归版本的形参表
void MergeSort(int arr[],int n)//参数和递归略不同,n代表数组中元素个数,即数组最大下标是n-1
{//非递归实现
/*
int step = 1;
while(step<n) //当元素个数不是2的幂时可能会出错,未考虑第2个序列个数不足的情况
{
for(int i=0;i<=n-step-1;i+=2*step)
Merge(arr,i,i+step-1,i+2*step-1);
step*=2;
}*/
int size=1,low,mid,high;
while(size<=n-1)
{
low=0;
while(low+size<=n-1)
{
mid=low+size-1;
high=mid+size;
if(high>n-1)//第二个序列个数不足size
high=n-1;
Merge(arr,low,mid,high);//调用归并子函数
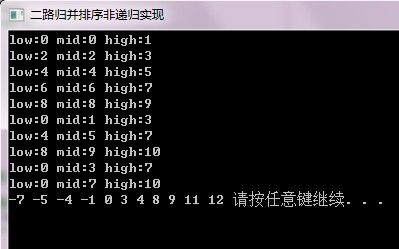
cout<<"low:"<<low<<" mid:"<<mid<<" high:"<<high<<endl;//打印出每次归并的区间
low=high+1;//下一次归并时第一关序列的下界
}
size*=2;//范围扩大一倍
}
}
int main()
{
int x[]={4,-5,0,3,-1,12,9,-7,8,-4,11};
MergeSort(x, 11);
for(int i=0;i<11;i++)
cout<<x[i]<<" ";
return 0;
}
图中的low mid high输出的是每次调用Merge函数时传的3个参数,便于分析每次合并所在的区间。