HDU 4565 So Easy! 递推数列+矩阵快速幂
题目链接点这儿
就是求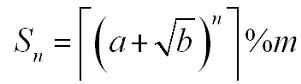 这个式子的值。。。第一眼。。。太鬼畜了。。。完全是不可做啊。。。
这个式子的值。。。第一眼。。。太鬼畜了。。。完全是不可做啊。。。
结果。。。练习赛过了会儿之后,,,有人做出来了。。。只好去瞪了。。。发现题目里有个条件(a-1)2< b < a2 也就是说a-1<sqrt(b)<a 这个有什么用呢。。我们可以凑一个跟所求式对称的式子 (a-sqrt(b))^n.。。。这个式子是小于1的,而且这个式子和所求式相加是一个整数(这个凑对称在和二项式相关的问题里还是经常用到的。。)那么Sn就是两个式子的值了。。。
那么,Sn = a^n+b^n。。。这很明显Sn有一个二阶常系数线性齐次的递推公式(一个差分方程),我们将它求出来之后,就可以用矩阵快速幂求第n项了。。
特征根为a+sqrt(b)和a-sqrt(b)。。。两个系数一个是2*a 一个是b-a^2(韦达定理求系数)然后只剩敲一个矩阵乘法了。。
下面放出代码
#include <vector>
#include <list>
#include <map>
#include <set>
#include <deque>
#include <queue>
#include <stack>
#include <bitset>
#include <algorithm>
#include <functional>
#include <numeric>
#include <utility>
#include <sstream>
#include <iostream>
#include <iomanip>
#include <cstdio>
#include <cmath>
#include <cstdlib>
#include <cctype>
#include <string>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <cstdlib>
#include <ctime>
#include <climits>
#define max(a,b) ((a)>(b)?(a):(b))
#define min(a,b) ((a)>(b)?(b):(a))
#define rep(i,initial_n,end_n) for(ll (i)=(initial_n);(i)<(end_n);i++)
#define repp(i,initial_n,end_n) for(ll (i)=(initial_n);(i)<=(end_n);(i)++)
#define reep(i,initial_n,end_n) for((i)=(initial_n);(i)<(end_n);i++)
#define reepp(i,initial_n,end_n) for((i)=(initial_n);(i)<=(end_n);(i)++)
#define eps 1.0e-9
#define MAX_N 1010
using namespace std;
typedef pair<int, int> pii;
typedef pair<double, double> pdd;
typedef __int64 ll;
typedef unsigned __int64 ull;
int main(){
ll a, b, n, m;
while(scanf("%I64d%I64d%I64d%I64d",&a,&b,&n,&m)!=EOF){
ll xishu[2][2]={2*a,b-a*a,1,0};
ll ans[2]={2*a,2};
while(n) {
if(n&1) {
ll a0,a1;
a0=(xishu[0][0]*ans[0]+xishu[0][1]*ans[1])%m;
a1=(xishu[1][0]*ans[0]+xishu[1][1]*ans[1])%m;
ans[0]=a0;
ans[1]=a1;
}
n/=2;
ll a0,a1,a2,a3;
a0=(xishu[0][0]*xishu[0][0]+xishu[0][1]*xishu[1][0])%m;
a1=(xishu[0][0]*xishu[0][1]+xishu[0][1]*xishu[1][1])%m;
a2=(xishu[1][0]*xishu[0][0]+xishu[1][1]*xishu[1][0])%m;
a3=(xishu[1][0]*xishu[0][1]+xishu[1][1]*xishu[1][1])%m;
xishu[0][0]=a0;
xishu[0][1]=a1;
xishu[1][0]=a2;
xishu[1][1]=a3;
}
printf("%I64d\n",(ans[1]+m)%m);
}
return 0;
}