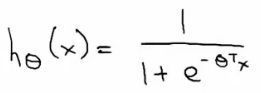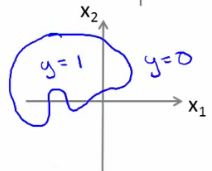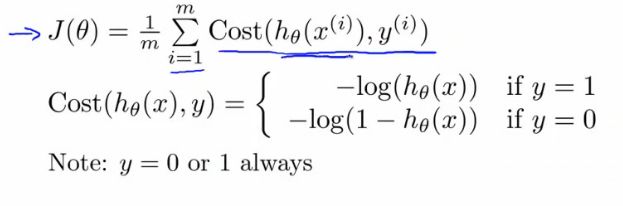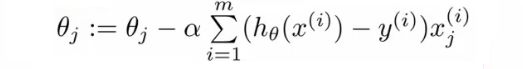Stanford Machine Learning: (2). Logistic_Regression

Classification

• Where y is a discrete value
  • Develop the logistic regression algorithm to determine what class a new input should fall into
• Classification problems
  • Email -> spam/not spam?
  • Online transactions -> fraudulent?
  • Tumor -> Malignant/benign
• Variable in these problems is Y
  • Y is either 0 or 1
    • 0 = negative class (absence of something)
    • 1 = positive class (presence of something)
• Start with binary class problems
  • Later look at multiclass classification problem, although this is just an extension of binary classification
• How do we develop a classification algorithm?
• • Tumour size vs malignancy (0 or 1)
  • We could use linear regression
  • • Then threshold the classifier output (i.e. anything over some value is yes, else no)
    • In our example below linear regression with thresholding seems to work
    • 
      

• We can see above this does a reasonable job of stratifying the data points into one of two classes
  • But what if we had a single Yes with a very small tumour 
  • This would lead to classifying all the existing yeses as nos
• Another issues with linear regression
  • We know Y is 0 or 1
  • Hypothesis can give values large than 1 or less than 0
• So, logistic regression generates a value where is always either 0 or 1
• • Logistic regression is a classification algorithm - don't be confused

Hypothesis representation

• What function is used to represent our hypothesis in classification
• We want our classifier to output values between 0 and 1
• • When using linear regression we did h_θ(x) = (θ^T x)
  • For classification hypothesis representation we do h_θ(x) = g((θ^T x))
  • • Where we define g(z)
      • z is a real number
    • g(z) = 1/(1 + e^-z)
      • This is the sigmoid function, or the logistic function
    • If we combine these equations we can write out the hypothesis as
    • 
      
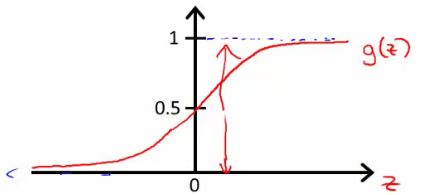
• What does the sigmoid function look like
• Crosses 0.5 at the origin, then flattens out]
  • Asymptotes at 0 and 1
  • 
    

• Given this we need to fit θ to our data

Interpreting hypothesis output

• When our hypothesis (h_θ(x)) outputs a number, we treat that value as the estimated probability that y=1 on input x
  • Example
    • If X is a feature vector with x₀ = 1 (as always) and x₁ = tumourSize
    • h_θ(x) = 0.7
      • Tells a patient they have a 70% chance of a tumor being malignant
  • We can write this using the following notation
    • h_θ(x) = P(y=1|x ; θ)
  • What does this mean?
    • Probability that y=1, given x, parameterized by θ
• Since this is a binary classification task we know y = 0 or 1
  • So the following must be true
    • P(y=1|x ; θ) + P(y=0|x ; θ) = 1
    • P(y=0|x ; θ) = 1 - P(y=1|x ; θ)

Decision boundary

• Gives a better sense of what the hypothesis function is computing
• Better understand of what the hypothesis function looks like
  • One way of using the sigmoid function is;
    
    • When the probability of y being 1 is greater than 0.5 then we can predict y = 1
    • Else we predict y = 0
  • When is it exactly that h_θ(x) is greater than 0.5?
    • Look at sigmoid function
      • g(z) is greater than or equal to 0.5 when z is greater than or equal to 0
        
    • So if z is positive, g(z) is greater than 0.5
      • z = (θ^T x)
    • So when 
      • θ^T x >= 0 
    • Then h_θ >= 0.5
• So what we've shown is that the hypothesis predicts y = 1 when θ^T x >= 0 
  • The corollary of that when θ^T x <= 0 then the hypothesis predicts y = 0 
  • Let's use this to better understand how the hypothesis makes its predictions

Decision boundary

• h_θ(x) = g(θ₀ + θ₁x₁ + θ₂x₂)

• So, for example
  • θ₀ = -3
  • θ₁ = 1
  • θ₂ = 1
• So our parameter vector is a column vector with the above values
  • So, θ^T is a row vector = [-3,1,1]
• What does this mean?
• • The z here becomes θ^T x
  • We predict "y = 1" if
    • -3x₀ + 1x₁ + 1x₂ >= 0
    • -3 + x₁ + x₂ >= 0
• We can also re-write this as
  • If (x₁ + x₂ >= 3) then we predict y = 1
  • If we plot
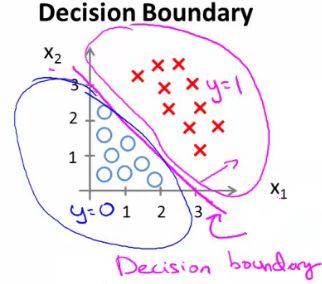
    • x₁ + x₂ = 3 we graphically plot our decision boundary

• Means we have these two regions on the graph
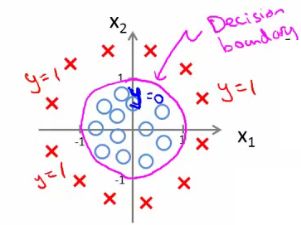
• • Blue = false
  • Magenta = true
  • Line = decision boundary
  • • Concretely, the straight line is the set of points where h_θ(x) = 0.5 exactly
  • The decision boundary is a property of the hypothesis
    • Means we can create the boundary with the hypothesis and parameters without any data
      • Later, we use the data to determine the parameter values
    • i.e. y = 1 if
      • 5 - x₁ > 0
      • 5 > x₁

Non-linear decision boundaries

• Get logistic regression to fit a complex non-linear data set
• • Like polynomial regress add higher order terms
  • So say we have
  • • h_θ(x) = g(θ₀ + θ₁x₁+ θ₃x₁² + θ₄x₂²)
    • We take the transpose of the θ vector times the input vector 
    • • Say θ^T was [-1,0,0,1,1] then we say;
      • Predict that "y = 1" if
      • • -1 + x₁² + x₂² >= 0
          or
        • x₁² + x₂² >= 1
      • If we plot x₁² + x₂² = 1
        • This gives us a circle with a radius of 1 around 0
        • 
          

• Mean we can build more complex decision boundaries by fitting complex parameters to this (relatively) simple hypothesis
• More complex decision boundaries?
• • By using higher order polynomial terms, we can get even more complex decision boundaries

Cost function for logistic regression

• Fit θ parameters
• Define the optimization object for the cost function we use the fit the parameters
• • Training set of m training examples
  • • Each example has is n+1 length column vector
    • 
      

• This is the situation
  • Set of m training examples
  • Each example is a feature vector which is n+1 dimensional
  • x₀ = 1
  • y ∈ {0,1}
  • Hypothesis is based on parameters (θ)
    • Given the training set how to we chose/fit θ?
• Linear regression uses the following function to determine θ
• 
  

• Instead of writing the squared error term, we can write
• • If we define "cost()" as;
    • cost(h_θ(xⁱ), y) = 1/2(h_θ(xⁱ) - yⁱ)²
    • Which evaluates to the cost for an individual example using the same measure as used in linear regression
  • We can redefine J(θ) as
  • 
    
    • Which, appropriately, is the sum of all the individual costs over the training data (i.e. the same as linear regression)
• To further simplify it we can get rid of the superscripts
  • So
    

• What does this actually mean?
  • This is the cost you want the learning algorithm to pay if the outcome is h_θ(x) and the actual outcome is y
  • If we use this function for logistic regression this is a non-convex function for parameter optimization
    • Could work....
• What do we mean by non convex?
• • We have some function - J(θ) - for determining the parameters
  • Our hypothesis function has a non-linearity (sigmoid function of h_θ(x) )
    • This is a complicated non-linear function
  • If you take h_θ(x) and plug it into the Cost() function, and them plug the Cost() function into J(θ) and plot J(θ) we find many local optimum -> non convex function
  • Why is this a problem
    • Lots of local minima mean gradient descent may not find the global optimum - may get stuck in a global minimum
  • We would like a convex function so if you run gradient descent you converge to a global minimum

A convex logistic regression cost function

• To get around this we need a different, convex Cost() function which means we can apply gradient descent
• 
  

• This is our logistic regression cost function
• • This is the penalty the algorithm pays
  • Plot the function
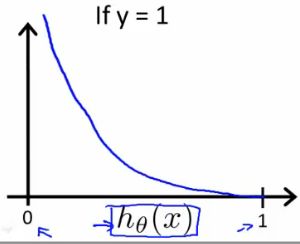
• Plot y = 1
• • So h_θ(x) evaluates as -log(h_θ(x))

• So when we're right, cost function is 0
  • Else it slowly increases cost function as we become "more" wrong
  • X axis is what we predict
  • Y axis is the cost associated with that prediction
• This cost functions has some interesting properties
  • If y = 1 and h_θ(x) = 1
    • If hypothesis predicts exactly 1 and thats exactly correct then that corresponds to 0 (exactly, not nearly 0)
  • As h_θ(x) goes to 0
    • Cost goes to infinity
    • This captures the intuition that if h_θ(x) = 0 (predict P (y=1|x; θ) = 0) but y = 1 this will penalize the learning algorithm with a massive cost
• What about if y = 0
• then cost is evaluated as -log(1- h_θ( x ))
• • Just get inverse of the other function
  • 
    

• Now it goes to plus infinity as h_θ(x) goes to 1
• With our particular cost functions J(θ) is going to be convex and avoid local minimum

Simplified cost function and gradient descent

• Define a simpler way to write the cost function and apply gradient descent to the logistic regression
  • By the end should be able to implement a fully functional logistic regression function
• Logistic regression cost function is as follows

• This is the cost for a single example
• • For binary classification problems y is always 0 or 1
  • • Because of this, we can have a simpler way to write the cost function
    • • Rather than writing cost function on two lines/two cases
      • Can compress them into one equation - more efficient 
  • Can write cost function is
    • cost(h_θ, (x),y) = -ylog( h_θ(x) ) - (1-y)log( 1- h_θ(x) ) 
      • This equation is a more compact of the two cases above
  • We know that there are only two possible cases
  • • y = 1
      • Then our equation simplifies to
        • -log(h_θ(x)) - (0)log(1 - h_θ(x))
          • -log(h_θ(x))
          • Which is what we had before when y = 1
    • y = 0
      • Then our equation simplifies to
        
        • -(0)log(h_θ(x)) - (1)log(1 - h_θ(x))
        • = -log(1- h_θ(x))
        • Which is what we had before when y = 0
    • Clever!
• So, in summary, our cost function for the θ parameters can be defined as
• 
  

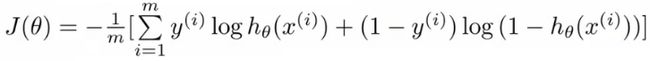
• Why do we chose this function when other cost functions exist?
  • This cost function can be derived from statistics using the principle of maximum likelihood estimation
    • Note this does mean there's an underlying Gaussian assumption relating to the distribution of features 
  • Also has the nice property that it's convex
• To fit parameters θ:
  • Find parameters θ which minimize J(θ)
  • This means we have a set of parameters to use in our model for future predictions
• Then, if we're given some new example with set of features x, we can take the θ which we generated, and output our prediction using
•     
          
• • This result is
  • • p(y=1 | x ; θ)
    • • Probability y = 1, given x, parameterized by θ

How to minimize the logistic regression cost function

• Now we need to figure out how to minimize J(θ)
• • Use gradient descent as before
  • Repeatedly update each parameter using a learning rate
  • 原始梯度更新：
  • 
    
  • 由于a和m都是常数，所以可以写成：
  • 
    

• If you had n features, you would have an n+1 column vector for θ
• This equation is the same as the linear regression rule
  • The only difference is that our definition for the hypothesis has changed
• Previously, we spoke about how to monitor gradient descent to check it's working
  • Can do the same thing here for logistic regression
• When implementing logistic regression with gradient descent, we have to update all the θ values (θ₀ to θ_n) simultaneously
  • Could use a for loop
  • Better would be a vectorized implementation
• Feature scaling for gradient descent for logistic regression also applies here

Advanced optimization

• Previously we looked at gradient descent for minimizing the cost function
• Here look at advanced concepts for minimizing the cost function for logistic regression
  • Good for large machine learning problems (e.g. huge feature set)
• What is gradient descent actually doing?
• • We have some cost function J(θ), and we want to minimize it
  • We need to write code which can take θ as input and compute the following
  • • J(θ)
    • Partial derivative if J(θ) with respect to j (where j=0 to j = n)
    • 
      

• Given code that can do these two things
  • Gradient descent repeatedly does the following update
  • 
    

• So update each j in θ sequentially
• So, we must;
  • Supply code to compute J(θ) and the derivatives
  • Then plug these values into gradient descent
• Alternatively, instead of gradient descent to minimize the cost function we could use
  • Conjugate gradient
  • BFGS (Broyden-Fletcher-Goldfarb-Shanno)
  • L-BFGS (Limited memory - BFGS)
• These are more optimized algorithms which take that same input and minimize the cost function
• These are very complicated algorithms
• Some properties
• • Advantages
    • No need to manually pick alpha (learning rate)
      • Have a clever inner loop (line search algorithm) which tries a bunch of alpha values and picks a good one
    • Often faster than gradient descent
      • Do more than just pick a good learning rate
    • Can be used successfully without understanding their complexity
  • Disadvantages
  • • Could make debugging more difficult
    • Should not be implemented themselves
    • Different libraries may use different implementations - may hit performance

Using advanced cost minimization algorithms

• How to use algorithms
• • Say we have the following example
  • 
    

• Example above
  • θ₁ and θ₂ (two parameters)
  • Cost function here is J(θ) = (θ₁ - 5)² + ( θ₂ - 5)²
  • The derivatives of the J(θ) with respect to either θ₁ and θ₂ turns out to be the 2(θ_i - 5)
• First we need to define our cost function, which should have the following signature

function [jval, gradent] = costFunction(THETA)

• Input for the cost function is THETA, which is a vector of the θ parameters
• Two return values from costFunction are
  • jval
    • How we compute the cost function θ (the underived cost function) 
      • In this case = (θ₁ - 5)² + (θ₂ - 5)²
  • gradient
    • 2 by 1 vector
    • 2 elements are the two partial derivative terms
    • i.e. this is an n-dimensional vector
      • Each indexed value gives the partial derivatives for the partial derivative of J(θ) with respect to θ_i
      • Where i is the index position in the gradient vector 
• With the cost function implemented, we can call the advanced algorithm using

options= optimset('GradObj', 'on', 'MaxIter', '100'); % define the options data structure

initialTheta= zeros(2,1); # set the initial dimensions for theta % initialize the theta values

[optTheta, funtionVal, exitFlag]= fminunc(@costFunction, initialTheta, options); % run the algorithm

• Here
• • options is a data structure giving options for the algorithm
  • fminunc
    • function minimize the cost function (find minimum of unconstrained multivariable function)
  • @costFunction is a pointer to the costFunction function to be used
• For the octave implementation
  • initialTheta must be a matrix of at least two dimensions 

• How do we apply this to logistic regression?
• • Here we have a vector 
  • 
    

• Here
  • theta is a n+1 dimensional column vector
  • Octave indexes from 1, not 0
• Write a cost function which captures the cost function for logistic regression

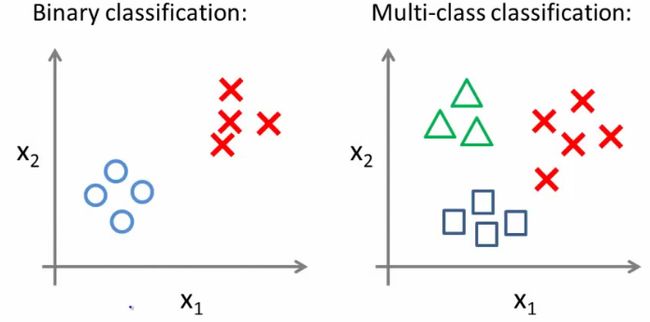
Multiclass classification problems

• Getting logistic regression for multiclass classification using one vs. all
• Multiclass - more than yes or no (1 or 0)
• • Classification with multiple classes for assignment

• Given a dataset with three classes, how do we get a learning algorithm to work?
• • Use one vs. all classification make binary classification work for multiclass classification
• One vs. all classification
• • Split the training set into three separate binary classification problems
  • • i.e. create a new fake training set
    • • Triangle (1) vs crosses and squares (0) h_θ¹(x)
        • P(y=1 | x₁; θ)
      • Crosses (1) vs triangle and square (0) h_θ²(x)
        • P(y=1 | x₂; θ)
      • Square (1) vs crosses and square (0) h_θ³(x)
        • P(y=1 | x₃; θ)

           

• Overal
• • Train a logistic regression classifier h_θ⁽ⁱ⁾(x) for each class i to predict the probability that y = i
  • On a new input, x to make a prediction, pick the class i that maximizes the probability that h_θ⁽ⁱ⁾(x) = 1