LCA 最近公共祖先 tarjan离线 总结 结合3个例题
在网上找了一些对tarjan算法解释较好的文章 并加入了自己的理解
LCA(Least Common Ancestor),顾名思义,是指在一棵树中,距离两个点最近的两者的公共节点。也就是说,在两个点通往根的道路上,肯定会有公共的节点,我们就是要求找到公共的节点中,深度尽量深的点。还可以表示成另一种说法,就是如果把树看成是一个图,这找到这两个点中的最短距离。
LCA算法有在线算法也有离线算法,所谓的在线算法就是实时性的,比方说,给你一个输入,算法就给出一个输出,就像是http请求,请求网页一样。给一个实时的请求,就返回给你一个请求的网页。而离线算法则是要求一次性读入所有的请求,然后在统一得处理。而在处理的过程中不一定是按照请求的输入顺序来处理的。说不定后输入的请求在算法的执行过程中是被先处理的。
本文先介绍一个离线的算法,就做tarjan算法。这个算法是基于并查集和DFS的。Dfs的作用呢,就是递归,一次对树中的每一个节点进行处理。而并查集的作用就是当dfs每访问完(注意,这里是访问完)到一个点的时候,就通过并查集将这个点,和它的子节点链接在一起构成一个集合,也就是将并查集中的pnt值都指向当前节点。这样就把树中的节点分成了若干个的集合,然后就是根据这些集合的情况来对输入数据来进行处理。
比方说当前访问到的节点是u,等u处理完之后呢,ancestor[u]就构成了u的集合中的点与u点的LCA,而ancestor[fa[u]]就构成了,u的兄弟节点及其兄弟子树的集合中点与u的LCA,而ancestor[fa[fa[u]]]就构成了u的父亲节点的兄弟节点及其兄弟子树的集合中的点与u的LCA。然后依次类推,这样就构成了这个LCA的离线算法。
以上来自 pursuit的专栏
首先,Tarjan算法是一种离线算法,也就是说,它要首先读入所有的询问(求一次LCA叫做一次询问),然后并不一定按照原来的顺序处理这些询问。而打乱这个顺序正是这个算法的巧妙之处。看完下文,你便会发现,如果偏要按原来的顺序处理询问,Tarjan算法将无法进行。
Tarjan算法是利用并查集来实现的。它按DFS的顺序遍历整棵树。对于每个结点x,它进行以下几步操作: * 计算当前结点的层号lv[x],并在并查集中建立仅包含x结点的集合,即root[x]:=x。 * 依次处理与该结点关联的询问。 * 递归处理x的所有孩子。 * root[x]:=root[father[x]](对于根结点来说,它的父结点可以任选一个,反正这是最后一步操作了)。
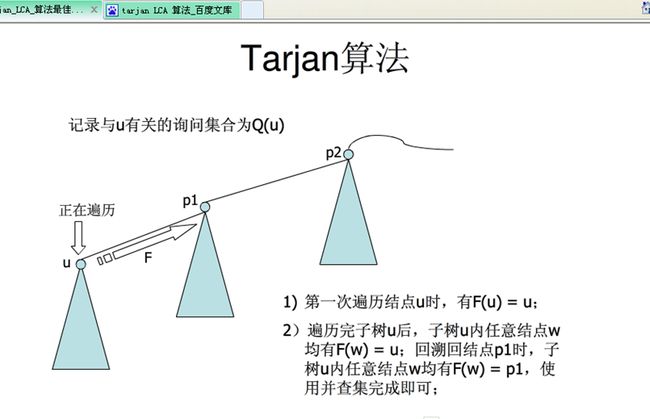
现在我们来观察正在处理与x结点关联的询问时并查集的情况。由于一个结点处理完毕后,它就被归到其父结点所在的集合,所以在已经处理过的结点中(包括 x本身),x结点本身构成了与x的LCA是x的集合,x结点的父结点及以x的所有已处理的兄弟结点为根的子树构成了与x的LCA是father[x]的集合,x结点的父结点的父结点及以x的父结点的所有已处理的兄弟结点为根的子树构成了与x的LCA是father[father[x]]的集合……(上面这几句话如果看着别扭,就分析一下句子成分,也可参照右面的图)假设有一个询问(x,y)(y是已处理的结点),在并查集中查到y所属集合的根是z,那么z 就是x和y的LCA,x到y的路径长度就是lv[x]+lv[y]-lv[z]*2。累加所有经过的路径长度就得到答案。 现在还有一个问题:上面提到的询问(x,y)中,y是已处理过的结点。那么,如果y尚未处理怎么办?其实很简单,只要在询问列表中加入两个询问(x, y)、(y,x),那么就可以保证这两个询问有且仅有一个被处理了(暂时无法处理的那个就pass掉)。而形如(x,x)的询问则根本不必存储。 如果在并查集的实现中使用路径压缩等优化措施,一次查询的复杂度将可以认为是常数级的,整个算法也就是线性的了。
根据TarjanLCA的实现算法可以看出,只有当某一棵子树全部遍历处理完成后,才将该子树的根节点标记为黑色(初始化是白色),假设程序按上面的树形结构进行遍历,首先从节点1开始,然后递归处理根为2的子树,当子树2处理完毕后,节点2, 5, 6均为黑色;接着要回溯处理3子树,首先被染黑的是节点7(因为节点7作为叶子不用深搜,直接处理),接着节点7就会查看所有询问(7, x)的节点对,假如存在(7, 5),因为节点5已经被染黑,所以就可以断定(7, 5)的最近公共祖先就是find(5).ancestor,即节点1(因为2子树处理完毕后,子树2和节点1进行了union,find(5)返回了合并后的树的根1,此时树根的ancestor的值就是1)。 有人会问如果没有(7, 5),而是有(5, 7)询问对怎么处理呢?我们可以在程序初始化的时候做个技巧,将询问对(a, b)和(b, a)全部存储,这样就能保证完整性
参考 applesun
下面这幅图可以让大家有个感性的认识 BY hnust_xiehonghao
下面是一个最基础的LCA题目 http://poj.org/problem?id=1330
赤裸裸的 题意 输入cas 后 有cas组数据 输入 n 再输入n-1 条边 之后输入x y 问x y的最近公共祖先是什么
#include<stdio.h>
#include<vector>
#include<string.h>
using namespace std;
#define Size 11111 //节点个数
vector<int> node[Size],que[Size];
int n,pare[Size],anse[Size],in[Size],rank[Size];
int vis[Size];
void init()
{
int i;
for(i=1;i<=n;i++)
{
node[i].clear();
que[i].clear();
rank[i]=1;
pare[i]=i;///
}
memset(vis,0,sizeof(vis));
memset(in,0,sizeof(in));
memset(anse,0,sizeof(anse));
}
int find(int nd)//并查集操作 不解释
{
return pare[nd]==nd?nd:pare[nd]=find(pare[nd]);
}
int Union(int nd1,int nd2)//并查集操作 不解释
{
int a=find(nd1);
int b=find(nd2);
if(a==b) return 0;
else if(rank[a]<=rank[b])
{
pare[a]=b;
rank[b]+=rank[a];
}
else
{
pare[b]=a;
rank[a]+=rank[b];
}
return 1;
}
void LCA(int root)
{
int i,sz;
anse[root]=root;//首先自成一个集合
sz=node[root].size();
for(i=0;i<sz;i++)
{
LCA(node[root][i]);//递归子树
Union(root,node[root][i]);//将子树和root并到一块
anse[find(node[root][i])]=root;//修改子树的祖先也指向root
}
vis[root]=1;
sz=que[root].size();
for(i=0;i<sz;i++)
{
if(vis[que[root][i]])
{
printf("%d\n",anse[find(que[root][i])]);///root和que[root][i]所表示的值的最近公共祖先
return ;
}
}
return ;
}
int main()
{
int cas,i;
scanf("%d",&cas);
while(cas--)
{
int s,e;
scanf("%d",&n);
init();
for(i=0;i<n-1;i++)
{
scanf("%d %d",&s,&e);
if(s!=e)
{
node[s].push_back(e);
// node[e].push_back(s);
in[e]++;
}
}
scanf("%d %d",&s,&e);
que[s].push_back(e);
que[e].push_back(s);
for(i=1;i<=n;i++) if(in[i]==0) break;//寻找根节点
// printf("root=%d\n",i);
LCA(i);
}
return 0;
}
之后来个加强版
http://acm.hdu.edu.cn/showproblem.php?pid=4547 CD操作 hdu4547
思路:
求出a和b的最近公共祖先,然后分4种情况讨论
①. a和b有一个公共祖先c,则用 c时间戳-a的时间戳+1(1步可以直接从c到b)
②. a是b的祖先,则只用1步就可以到达b点
③. b是a的祖先,则用a的时间戳-b的时间戳
④. a和b是同一个点,则答案是0
参考 http://www.cnblogs.com/Griselda/archive/2013/06/05/3119265.html
#include<stdio.h>
#include<vector>
#include<string.h>
#include<map>
#include<math.h>
#include<string>
using namespace std;
#define Size 111111 //节点个数
struct Query
{
int nd,id;
}temp;
struct out
{
int s,e;
}out[Size];
vector<int> node[Size];
vector<struct Query>que[Size];
int n,m,pare[Size],ance[Size],in[Size],rank[Size],dis[Size],ans[Size],vis[Size];
map<string,int>mp;
void init()
{
int i;
for(i=1;i<=n;i++)
{
node[i].clear();
que[i].clear();
rank[i]=1;
pare[i]=i;///
}
memset(vis,0,sizeof(vis));
memset(in,0,sizeof(in));
memset(ance,0,sizeof(ance));
memset(dis,0,sizeof(dis));
mp.clear();
}
int aabs(int aa)
{
if(aa>0) return aa;
else return -aa;
}
int find(int nd)//并查集操作 不解释
{
return pare[nd]==nd?nd:pare[nd]=find(pare[nd]);
}
int Union(int nd1,int nd2)//并查集操作 不解释
{
int a=find(nd1);
int b=find(nd2);
if(a==b) return 0;
else if(rank[a]<=rank[b])
{
pare[a]=b;
rank[b]+=rank[a];
}
else
{
pare[b]=a;
rank[a]+=rank[b];
}
return 1;
}
void LCA(int root,int num)
{
int i,sz;
ance[root]=root;//首先自成一个集合
dis[root]=num;
sz=node[root].size();
for(i=0;i<sz;i++)
{
LCA(node[root][i],num+1);//递归子树
Union(root,node[root][i]);//将子树和root并到一块
ance[find(node[root][i])]=root;//修改子树的祖先也指向root
}
vis[root]=1;
sz=que[root].size();
for(i=0;i<sz;i++)
{
int nd1,nd2,idx,ancestor;
nd1=root;nd2=que[root][i].nd;idx=que[root][i].id;
if(vis[nd2])
{
ans[idx]=ance[find(nd2)];
}
}
return ;
}
int main()
{
int cas,i;
scanf("%d",&cas);
while(cas--)
{
char ss[100],ee[100];
int s,e,cnt=1;
scanf("%d %d",&n,&m);
init();
for(i=0;i<n-1;i++)
{
scanf("%s %s",ee,ss);
if(mp.find(ss)==mp.end())
{
s=cnt;mp[ss]=cnt++;
}
else s=mp[ss];
if(mp.find(ee)==mp.end())
{
e=cnt;mp[ee]=cnt++;
}
else e=mp[ee];
if(s!=e)
{
node[s].push_back(e);
in[e]++;
}
}
for(i=0;i<m;i++)
{
scanf("%s %s",ss,ee);
s=mp[ss];e=mp[ee];
out[i].s=s;out[i].e=e;
temp.nd=e;temp.id=i;
que[s].push_back(temp);
temp.nd=s;temp.id=i;
que[e].push_back(temp);
}
for(i=1;i<=n;i++) if(in[i]==0) break;//寻找根节点
LCA(i,0);
for(i=0;i<m;i++)
{
if(out[i].s==out[i].e)
printf("0\n");
else
if(out[i].s==ans[i])
printf("1\n");
else if(out[i].e==ans[i])
printf("%d\n",dis[out[i].s]-dis[ans[i]]);
else
printf("%d\n",dis[out[i].s]-dis[ans[i]]+1);
}
}
return 0;
}
by hnust_xiehonghao
hdu 2874
http://acm.hdu.edu.cn/showproblem.php?pid=2874
题目大意: 给你一个n个节点m条边的森林,再给定q个查询,每次查询森林里两个点的最近距离。n ,m <= 10000,q <= 100万
本题和标准的LCA模板应用有了不小的区别 却可以让人更加透彻的看清LCA的思路 而且本题没有必要去求出公共祖先
具体看代码
#include<stdio.h>
#include<string.h>
#include<vector>
using namespace std;
#define Size 11111
struct Edge
{
int y,val;
}temp;
struct Query
{
int y,id;
}mid;
int pare[Size],ance[Size],vis[Size],dis[Size],rank[Size],ans[1000000+100],n,m,c,tree[Size];
vector<struct Query>que[Size];
vector<struct Edge>node[Size];
void init()
{
int i;
for(i=0;i<=n;i++)
{
vis[i]=0;
pare[i]=i;
dis[i]=0;
rank[i]=1;
que[i].clear();
node[i].clear();
}
memset(ans,-1,sizeof(ans));
}
int find(int x)
{
return pare[x]==x?x:pare[x]=find(pare[x]);
}
/*
void Union(int x,int y)
{
x=find(x);
y=find(y);
if(x!=y)
{
if(rank[x]>rank[y])
{
rank[x]+=rank[y];
pare[y]=x;
}
else
{
rank[y]+=rank[x];
pare[x]=y;
}
}
}
*/
void LCA(int root,int d,int k)//k表示是以第k个点作为根的树
{
int i,sz,nd1,nd2;
vis[root]=1; //已经遍历过的点 要标记一下 不要
tree[root]=k;dis[root]=d;
// ance[root]=root;
sz=node[root].size();
for(i=0;i<sz;i++)
{
nd2=node[root][i].y;
if(!vis[nd2])
{
LCA(nd2,d+node[root][i].val,k);
// Union(node[root][i].y,root);//用带rank的幷查集操作答案不对 不知道why
int w=find(nd2),m=find(root);
if(w!=m)
{
pare[w]=m;//这样才对
}
//ance[find(node[root][i].y)]=root;
}
}
sz=que[root].size();
for(i=0;i<sz;i++)
{
nd1=root;
nd2=que[root][i].y;
if(vis[nd2]&&tree[nd1]==tree[nd2])//如果 nd1 nd2 的跟是同一个点 则是同一棵树上的
{
ans[que[root][i].id]=dis[nd1]+dis[nd2]-2*dis[find(nd2)];
}
}
}
int main()
{
int i,j,x,y,val;
while(scanf("%d %d %d",&n,&m,&c)!=EOF)
{
init();
for(i=0;i<m;i++)
{
scanf("%d %d %d",&x,&y,&val);
if(x!=y)
{
temp.y=y;temp.val=val;
node[x].push_back(temp);
temp.y=x;
node[y].push_back(temp);//路是2个方向都可以通行的
}
}
for(i=0;i<c;i++)
{
scanf("%d %d",&x,&y);
mid.id=i;
mid.y=y;
que[x].push_back(mid);
mid.y=x;
que[y].push_back(mid);
}
for(i=1;i<=n;i++)
{
LCA(i,0,i);//以每一个节点作为根节点去深度搜索 找出每个点作为根的所有最近公共祖先
}
for(i=0;i<c;i++)
{
if(ans[i]==-1)
printf("Not connected\n");
else
printf("%d\n",ans[i]);
}
}
return 0;
}
/*本题给的是一个森林 而不是一颗树,由于在加入边的时候,我们让2个方向都能走 这样就
形成了一个强连通的快, 对于这个快来说,不管从快上那点出发 都可以遍历这个快上的所
有的点,且相对距离是一样的*/
待续 。。。。。。