矩阵分解之奇异值分解

矩阵分解之奇异值分解

引言

首先说矩阵，矩阵是一个难理解的数学描述，不管是在本科阶段的线性代数课上还是在研究生阶段的矩阵分析课上，都没有使我对矩阵产生什么好感，虽然考试也能过关，基本知识也能理解，但就是不知道有卵用。直到接触了机器学习相关算法论述时，发现好多的机器学习算法最终的描述都是通过矩阵分析相关知识推导而来，才知道了矩阵分析是非常有用的，但是到现在为止，还是没有什么好感。然后为什么要讲到奇异值分解，主要是在读《数学之美》中读到了采用奇异值分解解决文本分类问题的巧妙之处。首先在新闻分类中通过余弦定理计算新闻特征向量之间的夹角来对新闻进行分类或者聚类等操作，但对于网络上成千上万条新闻，通过余弦定理进行计算相关性运算量实在太大。而通过奇异值分解，可以实现将新闻特征矩阵分解为三个矩阵的乘积，而每个矩阵都有各自的含义，更为重要的是这三个矩阵的大小要比原来的特征矩阵小很多，从而在一定程度上减少了计算量。所以剩下的就是如何理解奇异值分解的含义，以及如何设计合适的算法实现奇异值分解了。奇异值分解的应用是本文的重点。

只记得在矩阵分析课中，有一章节是关于矩阵分解的，只考三个内容：满秩分解，奇异值分解和谱分解。实际上对于知识来讲并没有重要与否的区分，而是在哪里应用，什么时候用到。。。

概念

满秩分解：

A∈Cm×nr ，存在 B∈Cm×rr ， C∈Cr×nr ，满足 A=BC 。可用于求矩阵的伪逆，在最小二乘法中有应用（在线性回归中，如果得到的是欠定的方程，就需要用矩阵的伪逆来解决 pseudo inverse： CH(CCH)−1(BHB)−1BH, ）。

谱分解：

也叫特征值分解，将矩阵分解为由其特征值和特征向量表示的矩阵之积的方法。公式表示为：

A=Udiag(λ1,...,λn)UH=λ1α1αH1+λ2α2αH2+...+λnαnαHn

其中 λi 是特征值， αi 为对应的单位特征向量， α1αH1 是n阶矩阵。实际上就是将矩阵A分解为n个标准正交基，表示将矩阵A投影到这N个基构成的空间，对应的特征值为矩阵A在该空间上的坐标。

一个变换方阵的所有特征向量组成了这个变换矩阵的一组基。所谓基，可以理解为坐标系的轴。我们平常用到的大多是直角坐标系，在线性代数中可以把这个坐标系扭曲、拉伸、旋转，称为基变换。我们可以按需求去设定基，但是基的轴之间必须是线性无关的，也就是保证坐标系的不同轴不要指向同一个方向或可以被别的轴组合而成，否则的话原来的空间就“撑”不起来了。从线性空间的角度看，在一个定义了内积的线性空间里，对一个N阶对称方阵进行特征分解，就是产生了该空间的N个标准正交基，然后把矩阵投影到这N个基上。N个特征向量就是N个标准正交基，而特征值的模则代表矩阵在每个基上的投影长度。特征值越大，说明矩阵在对应的特征向量上的方差越大，功率越大，信息量越多。不过，特征值分解也有很多的局限，比如说变换的矩阵必须是方阵。

矩阵的乘法对应的是行列变换，实际上就是线性变换，可以发生伸缩、旋转、扭曲等变换，试想一下还记不记得图像空间变化中的仿射变换，用于图像的缩放、旋转和形变等，一个复杂的仿射变换实际上是有基础的简单的仿射变换通过矩阵连乘得到的。

特征值和特征向量的定义：设A是n阶方阵，如果存在 λ 和n维非零向量X，使 Ax=λx ，则 λ 称为方阵A的一个特征值，X为方阵A对应于或属于特征值 λ 的一个特征向量。

因此，特征向量的代数上含义是：将矩阵乘法转换为数乘操作；特征向量的几何含义是：特征向量通过方阵A变换只进行伸缩，而保持特征向量的方向不变。特征值表示的是这个特征到底有多重要，类似于权重，而特征向量在几何上就是一个点，从原点到该点的方向表示向量的方向。

美国数学家斯特让（G..Strang）在其经典教材《线性代数及其应用》中这样介绍了特征值作为频率的物理意义，他说：

大概最简单的例子（我从不相信其真实性，虽然据说1831年有一桥梁毁于此因）是一对士兵通过桥梁的例子。传统上，他们要停止齐步前进而要散步通过。这个理由是因为他们可能以等于桥的特征值之一的频率齐步行进，从而将发生共振。就像孩子的秋千那样，你一旦注意到一个秋千的频率，和此频率相配，你就使频率荡得更高。一个工程师总是试图使他的桥梁或他的火箭的自然频率远离风的频率或液体燃料的频率；而在另一种极端情况，一个证券经纪人则尽毕生精力于努力到达市场的自然频率线。特征值是几乎任何一个动力系统的最重要的特征。

其实，这个矩阵之所以能形成“频率的谱”，就是因为矩阵在特征向量所指的方向上具有对向量产生恒定的变换作用：增强（或减弱）特征向量的作用。进一步的，如果矩阵持续地叠代作用于向量，那么特征向量的就会凸现出来，实现的就是特征值的幂级数效果。

在机器学习特征提取中，意思就是最大特征值对应的特征向量方向上包含最多的信息量，如果某几个特征值很小，说明这几个方向信息量很小，可以用来降维，也就是删除小特征值对应方向的数据，只保留大特征值方向对应的数据，这样做以后数据量减小，但有用信息量变化不大，PCA降维就是基于这种思路。

奇异值分解

特征值分解是一个提取矩阵特征很不错的方法，但是它只适用于方阵。而在现实的世界中，我们看到的大部分矩阵都不是方阵，比如说有M个学生，每个学生有N科成绩，这样形成的一个 M×N 的矩阵就可能不是方阵，我们怎样才能像描述特征值一样描述这样一般矩阵呢的重要特征呢？奇异值分解就是用来干这个事的，奇异值分解是一个能适用于任意的矩阵的一种分解的方法。我们有必要先说说特征值和奇异值之间的关系。

对于特征值分解公式， ATA 是方阵，我们求 ATA 的特征值，即，此时求得的特征值就对应奇异值的平方，求得的特征向量v称为右奇异向量，另外还可以得到：

σi=λi−−√ui=Aviσi

ui 为左奇异值向量， σi 为奇异值。

假设A是一个N * M的矩阵，那么得到的U是一个N * N的方阵（里面的向量是正交的，U里面的向量称为左奇异向量），Σ是一个N * M的矩阵（除了对角线的元素都是0，对角线上的元素称为奇异值），V’(V的转置)是一个N * N的矩阵，里面的向量也是正交的，V里面的向量称为右奇异向量），从图片来反映几个相乘的矩阵的大小可得下面的图片

在矩阵Σ中也是从大到小排列，而且σ的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了。也就是说，我们也可以用前r大的奇异值来近似描述矩阵，这里定义一下部分奇异值分解：

r是一个远小于m、n的数，这样矩阵的乘法看起来像是下面的样子：

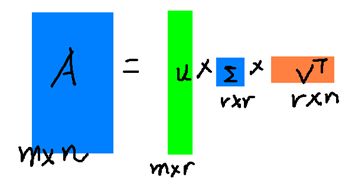
右边的三个矩阵相乘的结果将会是一个接近于A的矩阵，在这儿，r越接近于n，则相乘的结果越接近于A。而这三个矩阵的面积之和（在存储观点来说，矩阵面积越小，存储量就越小）要远远小于原始的矩阵A，我们如果想要压缩空间来表示原矩阵A，我们存下这里的三个矩阵：U、Σ、V就好了。

应用

下面讲解使用奇异值分解（SVD）的几个案例：

case 1： Data compression

一张 15 x 25 的图像数据：

主要由下面三部分构成：

表示成 15 x 25 的矩阵如下：

对矩阵M进行奇异值分解以后，得到奇异值分别是：

σ1=14.72σ2=5.22σ3=3.31

矩阵M就可以表示成： M=u1σ1vT1+u2σ2vT2+u3σ3vT3 ， vi 具有15个元素， ui 具有25个元素， σi 对应不同的奇异值。如上图所示，可以用123个元素来表示具有375个元素的图像数据了。也就是起到了data compression的效果。

值得说明的是为何这个大矩阵分解之后只有三个非零的奇异值(singular value)，因为实际上这些非零的奇异值个数代表正是这个矩阵的秩，所以，看看这幅图也就知道实际上只有三种不同的列，也就对应了矩阵的秩为3.

case 2： Noise reduction

前面的例子的奇异值都不为零，或者都还算比较大，下面我们来探索一下拥有零或者非常小的奇异值的情况。通常来讲，大的奇异值对应的部分会包含更多的信息。比如，我们有一张扫描的，带有噪声的图像，如下图所示：

采用跟实例二相同的处理方式处理该扫描图像。得到图像矩阵的奇异值：

σ1=14.15σ2=4.67σ3=3.00σ4=0.21σ5=0.19...σ15=0.05

很明显，前面三个奇异值远远比后面的奇异值要大，这样矩阵 M 的分解方式就可以如下：

M≈u1σ1vT1+u2σ2vT2+u3σ3vT3

经过奇异值分解后，得到了一张降噪后的图像：

case 3： Data analysis

搜集的数据中总是存在噪声：无论采用的设备多精密，方法有多好，总是会存在一些误差的。如果还记得上文提到的大的奇异值对应了矩阵中的主要信息的话，运用SVD进行数据分析，提取其中的主要部分的话，还是相当合理的。
作为例子，假如搜集的数据如下所示：

将数据用矩阵的形式表示：

经过奇异值分解后，得到 σ1=6.04,σ2=0.22
由于第一个奇异值远比第二个要大，数据中有包含一些噪声，第二个奇异值在原始矩阵分解相对应的部分可以忽略。经过SVD分解后，保留了主要样本点如图所示：

就保留主要样本数据来看，该过程跟PCA( principal component analysis)技术有一些联系，PCA也使用了SVD去检测数据间依赖和冗余信息.

case 4： 文本处理中的分类问题

最后就要分析在《数学之美》之美的矩阵计算与文本处理中的分类问题一章节中，吴军老师讲到：

“三个矩阵有非常清楚的物理含义。第一个矩阵X中的每一行表示意思相关的一类词，其中的每个非零元素表示这类词中每个词的重要性（或者说相关性），数值越大越相关。最后一个矩阵Y中的每一列表示同一主题一类文章，其中每个元素表示这类文章中每篇文章的相关性。中间的矩阵则表示词的类和文章的类之间的相关性。因此，我们只要对关联矩阵A进行一次奇异值分解，可以同时完成了近义词分类和文章的分类。（同时得到每类文章和每类词的相关性）。”

实际上在读的时候我是没有理解的，这是潜在语义索引（Latent Semantic Indexing）的精髓内容，下面借用一个博客中的例子说明下：

一行表示一个词在哪些title中出现了（一行就是之前说的一维feature），一列表示一个title中有哪些词。比如说T1这个title中就有guide、investing、market、stock四个词，各出现了一次，将这个矩阵进行SVD，得到下面的矩阵：

左奇异向量表示词的一些特性，右奇异向量表示文档的一些特性，中间的奇异值矩阵表示左奇异向量的一行与右奇异向量的一列的重要程度，数字越大越重要。
继续看这个矩阵还可以发现一些有意思的东西，首先，左奇异向量的第一列表示每一个词的出现频繁程度，虽然不是线性的，但是可以认为是一个大概的描述，比如book是0.15对应文档中出现的2次，investing是0.74对应了文档中出现了9次，rich是0.36对应文档中出现了3次；其次，右奇异向量中一的第一行表示每一篇文档中的出现词的个数的近似，比如说，T6是0.49，出现了5个词，T2是0.22，出现了2个词。
将左奇异向量和右奇异向量都取后2维（之前是3维的向量，直接取后两维度），投影到一个平面上，可以得到：

在图上，每一个红色的点，都表示一个词，每一个蓝色的点，都表示一篇文档，这样我们可以对这些词和文档进行聚类，比如说stock 和 market可以放在一类，因为他们老是出现在一起，real和estate可以放在一类，dads，guide这种词就看起来有点孤立了，我们就不对他们进行合并了。按这样聚类出现的效果，可以提取文档集合中的近义词，这样当用户检索文档的时候，是用语义级别（近义词集合）去检索了，而不是之前的词的级别。一是减少我们的检索、存储量，因为这样压缩的文档集合和PCA是异曲同工的；二是可以提高我们的用户体验，用户输入一个词，我们可以在这个词的近义词的集合中去找，这是传统的索引无法做到的。

case 5： 奇异值分解在PCA中的应用

首先简单说明一下主成分分析（principal component analysis）的过程：对原始的空间中顺序地找一组相互正交的坐标轴，第一个轴是使得方差最大的，第二个轴是在与第一个轴正交的平面中使得方差最大的，第三个轴是在与第1、2个轴正交的平面中方差最大的，这样假设在N维空间中，我们可以找到N个这样的坐标轴，我们取前r个去近似这个空间，这样就从一个N维的空间压缩到r维的空间了，但是我们选择的r个坐标轴能够使得空间的压缩使得数据的损失最小。

一般来说，方差大的方向是信号的方向，方差小的方向是噪声的方向，我们在数据挖掘中或者数字信号处理中，往往要提高信号与噪声的比例，也就是信噪比。对上图来说，如果我们只保留signal方向的数据，也可以对原数据进行不错的近似了。

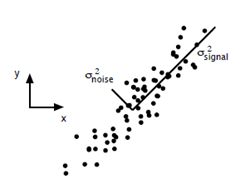
如上图所示，假设是一个摄像机采集一个物体运动得到的图片，上面的点表示物体运动的位置，假如我们想要用一条直线去拟合这些点，那我们会选择什么方向的线呢？当然是图上标有signal的那条线。如果我们把这些点单纯的投影到x轴或者y轴上，最后在x轴与y轴上得到的方差是相似的（因为这些点的趋势是在45度左右的方向，所以投影到x轴或者y轴上都是类似的），如果我们使用原来的xy坐标系去看这些点，容易看不出来这些点真正的方向是什么。但是如果我们进行坐标系的变化，横轴变成了signal的方向，纵轴变成了noise的方向，则就很容易发现什么方向的方差大，什么方向的方差小了。

假设我们矩阵每一行表示一个样本，每一列表示一个feature，用矩阵的语言来表示，将一个 m×n 的矩阵A的进行坐标轴的变化，P就是一个变换的矩阵从一个N维的空间变换到另一个N维的空间，在空间中就会进行一些类似于旋转、拉伸的变化。

而将一个 m×n 的矩阵A变换成一个 m×r 的矩阵，这样就会使得本来有n个feature的，变成了有r个feature了（r < n)，这r个其实就是对n个feature的一种提炼，我们就把这个称为feature的压缩。用数学语言表示就是：

但是这个怎么和SVD扯上关系呢？之前谈到，SVD得出的奇异向量也是从奇异值由大到小排列的，按PCA的观点来看，就是方差最大的坐标轴就是第一个奇异向量，方差次大的坐标轴就是第二个奇异向量…我们回忆一下之前得到的SVD式子：

在矩阵的两边同时乘上一个矩阵V，由于V是一个正交的矩阵，所以V转置乘以V得到单位阵I，所以可以化成后面的式子:

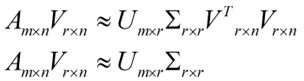
将后面的式子与A * P那个m * n的矩阵变换为m * r的矩阵的式子对照看看，在这里，其实V就是P，也就是一个变化的向量。这里是将一个m * n 的矩阵压缩到一个m * r的矩阵，也就是对列进行压缩，如果我们想对行进行压缩（在PCA的观点下，对行进行压缩可以理解为，将一些相似的sample合并在一起，或者将一些没有太大价值的sample去掉）怎么办呢？同样我们写出一个通用的行压缩例子：

这样就从一个m行的矩阵压缩到一个r行的矩阵了，对SVD来说也是一样的，我们对SVD分解的式子两边乘以U的转置U’

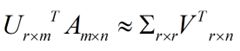
这样我们就得到了对行进行压缩的式子。可以看出，其实PCA几乎可以说是对SVD的一个包装，如果我们实现了SVD，那也就实现了PCA了，而且更好的地方是，有了SVD，我们就可以得到两个方向的PCA，如果我们对A’A进行特征值的分解，只能得到一个方向的PCA。

参考文献：
http://www.ams.org/samplings/feature-column/fcarc-svd
http://www.puffinwarellc.com/index.php/news-and-articles/articles/33-latent-semantic-analysis-tutorial.html
http://www.miislita.com/information-retrieval-tutorial/svd-lsi-tutorial-1-understanding.html
http://blog.csdn.net/redline2005/article/details/24100293
http://www.cnblogs.com/liangflying/archive/2012/09/25/2701148.html

2015-9-15 艺少