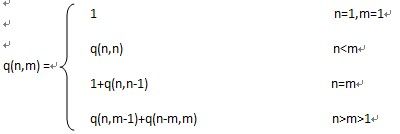0002算法笔记——【递归】排列问题，整数划分问题，Hanoi问题

       递归的概念想必大家都清楚，概念神马的直接略过。这里介绍递归相关的几个问题。

    1、排列问题

    设R={r1,r2,...,rn}是要进行排列的n个元素，Ri=R-{ri}。集合x中元素的全排列记为Perm(X)。(ri)Perm(X)表示在全排列Perm(X)的每一个排列前加上前缀ri得到的排列。R的全排列可归纳如下：

    当n=1时，Perm(R)=(r)，其中r是集合中唯一的元素；

    当n>1时，Perm(R)由(r1)Perm(R1),(r2)Perm(R2),(r3)Perm(R3)。。。。(rn)Perm(Rn)构成。

    程序代码：

//2-4 排列问题
#include "stdafx.h"
#include <iostream>     
using namespace std; 

template <class Type>
inline void Swap(Type &a,Type &b);

template <class Type>
void Perm(Type list[],int k,int m);

int main()
{
	int list[3];
	for(int i=0; i<3;i++)
	{
		list[i] = i+1;
	}
	Perm(list,0,2);
	return 0;
}

template <class Type>
inline void Swap(Type &a,Type &b)
{
	Type temp = a;
	a = b;
	b = temp;
}

template <class Type>
void Perm(Type list[],int k,int m)
{
	//只剩下一个元素
	if(k == m){
		for(int i=0; i<=m; i++)
		{
			cout<<list[i]<<" ";
		}
		cout<<endl;
	}
	else
	{
		//将list[k:m}中的每一个元素分别与list[k]中的元素交换
		//然后递归计算list[k+1:m]的全排列，将计算结果作为list[0:k]后缀
		for(int i=k; i<=m;i++){
			Swap(list[k],list[i]);
			Perm(list,k+1,m);
			Swap(list[k],list[i]);
		}
	}
}

       运行结果：

2、整数划分问题

    将正整数n表示成一系列正整数之和，n=n1+n2+n3+......nk(其中，n1>=n2>=......nk>=1,k>=1),正整数n的这种表示称为正整数n的划分。正整数n的不同划分个数称为正整数n的划分数,记作p(n)。例如：正整数6有11总不同的划分

6;

5+1;

4+2,4+1+1;

3+3,3+2+1,3+1+1+1;

2+2+2,2+2+1+1,2+1+1+1+1;

1+1+1+1+1+1;

记q(n,m)为正整数n的所有不同划分中，最大加数n1不大于m的划分个数。可以建立如下递推关系:

前面三个递推式比较好理解，关键是第四个递推式。当n>m>1时，n的划分由两部分组成。以整数q(6,3)为例，q(n,m-1)内容是第5排和第6排内容，不大于2的6的划分；q(n-m,m)内容是第4排,不大于3的(6-3=3)的划分。

程序代码：

//2-4 整数划分问题
#include "stdafx.h"
#include <iostream>     
using namespace std;

int q(int n,int m);

int main(){
	cout<<q(6,6)<<endl;
	return 0;
}

int q(int n,int m)
{
	if( n<1 || m<1)
	{
		return 0;
	}
	else if(n==1 || m==1)
	{
		return 1;
	}
	else if(n<m)
	{
		return q(n,n);
	}
	else if(n==m)
	{
		return q(n,m-1) + 1;
	}
	else
	{
		return q(n,m-1) + q(n-m,m);
	}
}

3、汉诺塔问题

     这个问题大家都比较熟悉。这里直接给出程序清单。

//2-6 Hanoi问题
#include "stdafx.h"
#include <iostream>     
using namespace std;

void hanoi(int n,char a,char b,char c);

int main(){
	char a = 'A',b = 'B',c='C';
	hanoi(3,a,b,c);
	return 0;
}

//借助c,将n个盘子从a移到b
void hanoi(int n,char a,char b,char c)
{
	if(n>0)
	{
		hanoi(n-1,a,c,b);//借助b,将n-1个盘子从a移到c
		cout<<"将"<<a<<"中最大的盘子从"<<a<<"移到"<<b<<endl;
		hanoi(n-1,c,b,a);//借助a，将n-1个盘子从c移到b
	}
}