中值滤波器(Median filter)特性及其实现
中值滤波器(Median filter)特性及其实现
信号处理时经常要做的一件事就是滤波,其中线性滤波器比如FIR、IIR 等类型都是研究的比较透彻的,实际使用中也有很好的效果。但是有时我们遇到的信号的噪声比较顽固,比如说电子信号中的爆米花噪声(popcorn noise)还有图像处理中的椒盐噪声(salt-and-pepper noise),用普通的线性滤波器只能将其压低,而无法彻底消除。这时一些非线性滤波器就体现出优势来了。比如说今天要介绍的中值滤波器。
中值滤波器在图像处理领域用的比较多,其实这种滤波器也可以用于一维信号,有时甚至能起到意想不到的效果。
基本原理
中值滤波器的想法很简单,如果一个信号是平缓变化的,那么某一点的输出值可以用这点的某个大小的邻域内的所有值的统计中值来代替。这个邻域在信号处理领域称之为窗(window)。窗开的越大,输出的结果就越平滑,但也可能会把我们有用的信号特征给抹掉。所以窗的大小要根据实际的信号和噪声特性来确定。
通常我们会选择窗的大小使得窗内的数据个数为奇数个,之所以这么选是因为奇数个数据才有唯一的中间值。
边界值的处理方法
对于有限长的数据,自然会存在两个边界,对于边界的处理有很多种方法,常见的方法有:
- 不处理边界的数据,原样输出。
- 将边界值重复。
- 前后补 0。
- 在边界时缩小窗的大小。
C++ 代码
下面给出一个 C++ 写的代码。首先既然要求中值,那么就要对数据进行排序。通常情况下我们中值滤波器的 window 不会很大,所以也不需要快速排序法这样的比较高级的排序方法。我就只简单的写了个冒泡排序法。大家也可以换用其他的排序方法。
bubbleSort 函数用来升序排序,代码如下:
template <typename Type> inline void bubbleSort(Type data[], int size)
{
Type temp;
while(size > 1)
{
for(int i = 0; i < size - 1; i++)
{
if(data[i] > data[i + 1])
{
temp = data[i];
data[i] = data[i + 1];
data[i + 1] = temp;
}
}
size --;
}
}
当然在排序之前还要有个数据拷贝函数,我没有直接用 memcpy 这样的函数,而是自己写了个简单的。其实用 memcpy 也挺好。
template <typename Type> static inline void copy(Type input[], Type buf[], int left_bound, int kernel_size)
{
for(int i = 0; i < kernel_size; i ++)
{
buf[i] = input[left_bound + i];
}
}
有了这些基础之后就可以实现我们的中值滤波器了。这里对边界数据的处理办法是在边界处缩小 window。对于第一个数据和最后一个数据,window 缩小到 1。第二个数据 window 为 3,第三个数据 window 为 5,以此类推,直到 window 达到设定大小。
/**
* @brief medianFilter 中值滤波器
* @param data 输入数据
* @param size 输入数据的元素数量
* @param kernel_size 滤波器大小,最好为奇数
* @param buf 函数内部使用的数组,如果为 NULL 则函数内部分配空间。
*/
template <typename Type> void medianFilter(Type input[], Type output[], int size, int kernel_size, Type buf[])
{
bool newBuf = false;
if(buf == 0)
{
newBuf = true;
buf = new Type[kernel_size];
}
int half = kernel_size / 2;
int end = size - half;
for(int pos = 0; pos < half; pos ++)
{
int part = 2 * pos + 1;
copy(input, buf, 0, part);
bubbleSort(buf, part);
output[pos] = buf[part / 2];
}
int left_bound = 0;
for(int pos = half; pos < end; pos ++)
{
copy(input, buf, left_bound, kernel_size);
left_bound ++;
bubbleSort(buf, kernel_size);
output[pos] = buf[half];
}
left_bound ++;
for(int pos = end; pos < size; pos ++)
{
int part = 2 * (size - pos) - 1;
copy(input, buf, left_bound, part);
left_bound += 2;
bubbleSort(buf, part);
output[pos] = buf[part / 2];
}
if(newBuf)
{
delete[] buf;
}
}
下面是个测试代码,为了方便,用到了些 Qt 的功能。
int main(int argc, char *argv[])
{
//QCoreApplication a(argc, argv);
double d[40], e[40];
for(int i = 0; i < 40; i ++)
{
d[i] = 0.01 * (i - 20) * (i - 20);
}
d[3] = 10;
d[15] = -3;
d[25] = 20;
d[30] = -20;
//bubbleSort(d, 12);
medianFilter(d, e, 40, 9, (double *)NULL);
QFile data("Q:\\output.txt");
if (data.open(QFile::WriteOnly | QFile::Truncate))
{
QTextStream out(&data);
for(int i = 0; i < 40; i ++)
{
out << d[i] << ", " << e[i] << endl;
}
}
qDebug() << "Hello";
//return a.exec();
}
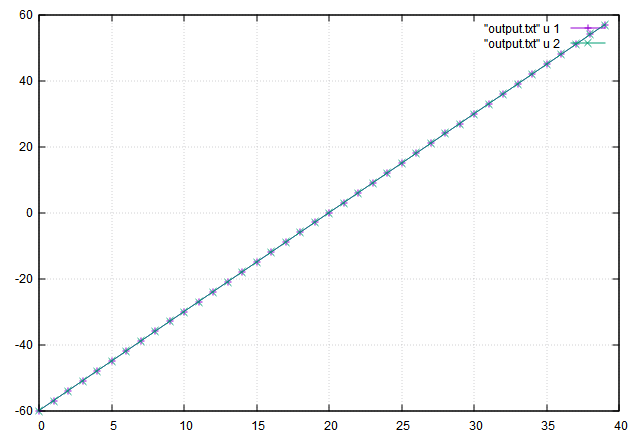
这个代码还有个很好的特性。就是不改变线性数据的滤波结果。下面是个例子。
int main(int argc, char *argv[])
{
double d[40], e[40];
for(int i = 0; i < 40; i ++)
{
d[i] = 3 * (i - 20);
}
medianFilter(d, e, 40, 9, (double *)NULL);
QFile data("Q:\\output.txt");
if (data.open(QFile::WriteOnly | QFile::Truncate))
{
QTextStream out(&data);
for(int i = 0; i < 40; i ++)
{
out << d[i] << ", " << e[i] << endl;
}
}
}