基于PCL库对三维空间点的K-Means聚类算法的实现
K-Means算法简介
K-Means算法是一种常用的聚类算法,因其思想简单、容易实现而收到广泛的运用。其思想大概是从要聚类的样本中选取K个样本,然后遍历所有样本,对每个样本计算其与K个样本间的距离(可以为欧氏距离或余弦距离),然后将其类别归为距离最小的样本所属类别,这样的话,所有样本就都找到各自所属的类别;然后分别重新计算K个类别中样本的质心;之后返回第一步继续迭代执行,如此直到K个类别中样本的质心不再移动或移动的非常小。整个过程往往要不了几次就达到收敛。
基于PCL库对三维空间点的K-Means聚类算法的实现
在三维点云处理中我们经常要对点云进行聚类分割处理,如建筑物与地面、桌面与水杯等的分割,以便于我们可以在后续三维重建中得到更好的效果。这时比较好的聚类方法有欧式聚类和K-Means聚类。这里简要地介绍下基于PCL库对三维空间点的K-Means聚类算法的实现。
相关头文件common.h中部分内容
//笛卡尔坐标系中三维点坐标
typedef struct st_pointxyz
{
float x;
float y;
float z;
}st_pointxyz;
typedef struct st_point
{
st_pointxyz pnt;
int groupID;
st_point()
{
}
st_point(st_pointxyz &p, int id)
{
pnt = p;
groupID = id;
}
}st_point;
class KMeans
{
public:
int m_k;
typedef std::vector<st_point> VecPoint_t;
VecPoint_t mv_pntcloud; //要聚类的点云
std::vector<VecPoint_t> m_grp_pntcloud; //K类,每一类存储若干点
std::vector<st_pointxyz> mv_center; //每个类的中心
KMeans()
{
m_k = 0;
}
inline void SetK(int k_)
{
m_k = k_;
m_grp_pntcloud.resize(m_k);
}
//设置输入点云
bool SetInputCloud(PointCloud<PointXYZ>::Ptr pPntCloud);
//初始化最初的K个类的中心
bool InitKCenter(st_pointxyz pc_arr[]);
//聚类
bool Cluster();
//更新K类的中心
bool UpdateGroupCenter(std::vector<VecPoint_t> &grp_pntcloud, std::vector<st_pointxyz> ¢er);
//计算两个点间的欧氏距离
double DistBetweenPoints(st_pointxyz &p1, st_pointxyz &p2);
//是否存在中心点移动
bool ExistCenterShift(std::vector<st_pointxyz> &prev_center, std::vector<st_pointxyz> &cur_center);
//将聚类的点分别存到各自的pcd文件中
bool SaveFile(const char *prex_name);
//将聚类的点分别存到各自的pcd文件中
bool SaveFile(const char *dir_name, const char *prex_name);
};
实现文件kmeans.cpp中内容为:
#include "common.h"
const float DIST_NEAR_ZERO = 0.001;
extern char szFileName[256];
bool KMeans::InitKCenter(st_pointxyz pnt_arr[])
{
if (m_k == 0)
{
PCL_ERROR("在此之前必须要调用setK()函数\n");
return false;
}
mv_center.resize(m_k);
for (size_t i = 0; i < m_k; ++i)
{
mv_center[i] = pnt_arr[i];
}
return true;
}
bool KMeans::SetInputCloud(PointCloud<PointXYZ>::Ptr pPntCloud)
{
size_t pntCount = (size_t)pPntCloud->points.size();
//mv_pntcloud.resize(pntCount);
for (size_t i = 0; i < pntCount; ++i)
{
st_point point;
point.pnt.x = pPntCloud->points[i].x;
point.pnt.y = pPntCloud->points[i].y;
point.pnt.z = pPntCloud->points[i].z;
point.groupID = 0;
mv_pntcloud.push_back(point);
}
return true;
}
bool KMeans::Cluster()
{
std::vector<st_pointxyz> v_center(mv_center.size());
do
{
for (size_t i = 0, pntCount = mv_pntcloud.size(); i < pntCount; ++i)
{
double min_dist = DBL_MAX;
int pnt_grp = 0;
for (size_t j = 0; j < m_k; ++j)
{
double dist = DistBetweenPoints(mv_pntcloud[i].pnt, mv_center[j]);
if (min_dist - dist > 0.000001)
{
min_dist = dist;
pnt_grp = j;
}
}
m_grp_pntcloud[pnt_grp].push_back(st_point(mv_pntcloud[i].pnt, pnt_grp));
}
//保存上一次迭代的中心点
for (size_t i = 0; i < mv_center.size(); ++i)
{
v_center[i] = mv_center[i];
}
if (!UpdateGroupCenter(m_grp_pntcloud, mv_center))
{
return false;
}
if ( !ExistCenterShift(v_center, mv_center))
{
break;
}
for (size_t i = 0; i < m_k; ++i){
m_grp_pntcloud[i].clear();
}
}while(true);
return true;
}
double KMeans::DistBetweenPoints(st_pointxyz &p1, st_pointxyz &p2)
{
double dist = 0;
double x_diff = 0, y_diff = 0, z_diff = 0;
x_diff = p1.x - p2.x;
y_diff = p1.y - p2.y;
z_diff = p1.z - p2.z;
dist = sqrt(x_diff * x_diff + y_diff * y_diff + z_diff * z_diff);
return dist;
}
bool KMeans::UpdateGroupCenter(std::vector<VecPoint_t> &grp_pntcloud, std::vector<st_pointxyz> ¢er)
{
if (center.size() != m_k)
{
PCL_ERROR("类别的个数不为K\n");
return false;
}
for (size_t i = 0; i < m_k; ++i)
{
float x = 0, y = 0, z = 0;
size_t pnt_num_in_grp = grp_pntcloud[i].size();
for (size_t j = 0; j < pnt_num_in_grp; ++j)
{
x += grp_pntcloud[i][j].pnt.x;
y += grp_pntcloud[i][j].pnt.y;
z += grp_pntcloud[i][j].pnt.z;
}
x /= pnt_num_in_grp;
y /= pnt_num_in_grp;
z /= pnt_num_in_grp;
center[i].x = x;
center[i].y = y;
center[i].z = z;
}
return true;
}
//是否存在中心点移动
bool KMeans::ExistCenterShift(std::vector<st_pointxyz> &prev_center, std::vector<st_pointxyz> &cur_center)
{
for (size_t i = 0; i < m_k; ++i)
{
double dist = DistBetweenPoints(prev_center[i], cur_center[i]);
if (dist > DIST_NEAR_ZERO)
{
return true;
}
}
return false;
}
//将聚类的点分别存到各自的pcd文件中
bool KMeans::SaveFile(const char *prex_name)
{
for (size_t i = 0; i < m_k; ++i)
{
pcl::PointCloud<pcl::PointXYZ>::Ptr p_pnt_cloud(new pcl::PointCloud<pcl::PointXYZ> ());
for (size_t j = 0, grp_pnt_count = m_grp_pntcloud[i].size(); j < grp_pnt_count; ++j)
{
pcl::PointXYZ pt;
pt.x = m_grp_pntcloud[i][j].pnt.x;
pt.y = m_grp_pntcloud[i][j].pnt.y;
pt.z = m_grp_pntcloud[i][j].pnt.z;
p_pnt_cloud->points.push_back(pt);
}
p_pnt_cloud->width = (int)m_grp_pntcloud[i].size();
p_pnt_cloud->height = 1;
char newFileName[256] = {0};
char indexStr[16] = {0};
strcat(newFileName, szFileName);
strcat(newFileName, "-");
strcat(newFileName, prex_name);
strcat(newFileName, "-");
sprintf(indexStr, "%d", i + 1);
strcat(newFileName, indexStr);
strcat(newFileName, ".pcd");
savePCDFileASCII(newFileName, *p_pnt_cloud);
}
return true;
}
bool KMeans::SaveFile(const char *dir_name, const char *prex_name)
{
for (size_t i = 0; i < m_k; ++i)
{
pcl::PointCloud<pcl::PointXYZ>::Ptr p_pnt_cloud(new pcl::PointCloud<pcl::PointXYZ> ());
for (size_t j = 0, grp_pnt_count = m_grp_pntcloud[i].size(); j < grp_pnt_count; ++j)
{
pcl::PointXYZ pt;
pt.x = m_grp_pntcloud[i][j].pnt.x;
pt.y = m_grp_pntcloud[i][j].pnt.y;
pt.z = m_grp_pntcloud[i][j].pnt.z;
p_pnt_cloud->points.push_back(pt);
}
p_pnt_cloud->width = (int)m_grp_pntcloud[i].size();
p_pnt_cloud->height = 1;
char newFileName[256] = {0};
char indexStr[16] = {0};
strcat(newFileName, dir_name);
strcat(newFileName, "/");
strcat(newFileName, prex_name);
strcat(newFileName, "-");
sprintf(indexStr, "%d", i + 1);
strcat(newFileName, indexStr);
strcat(newFileName, ".pcd");
savePCDFileASCII(newFileName, *p_pnt_cloud);
}
return true;
}
下面编写测试用例,测试效果:
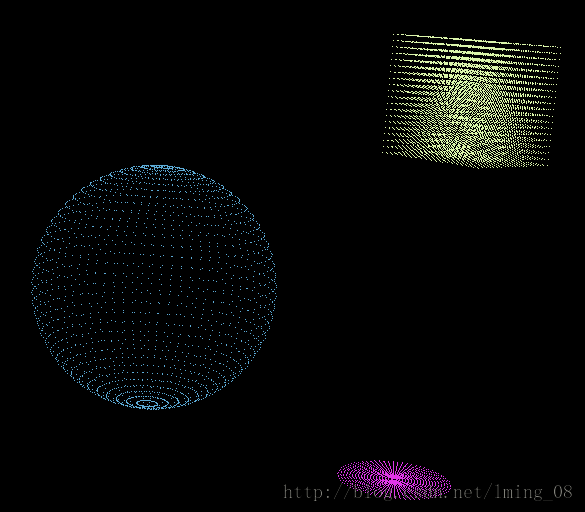
构造一个以(0, 0, 0)为球心,半径为2的球体;一个左下角坐标为(2.5, 2.5, 2.5),棱长为2的正方体;一个圆心为(1, 1, -3),半径为1的圆。然后初始类的中心分别为上述三个体的中心,并执行K-Means聚类算法,将聚类后的点云数据分别保存到对应的文件中。代码如下:
void test_kmeans_manual_consdata()
{
//构造球体
float radius = 2;
for (float r = 0; r < radius; r += 0.1)
{
for (float angle1 = 0.0; angle1 <= 180.0; angle1 += 5.0)
{
for (float angle2 = 0.0; angle2 <= 360.0; angle2 += 5.0)
{
pcl::PointXYZ basic_point;
basic_point.x = radius * sinf(pcl::deg2rad(angle1)) * cosf(pcl::deg2rad(angle2));
basic_point.y = radius * sinf(pcl::deg2rad(angle1)) * sinf(pcl::deg2rad(angle2));
basic_point.z = radius * cosf(pcl::deg2rad(angle1));
cloud->points.push_back(basic_point);
}
}
}
//构造立方体
float cube_len = 2;
for (float x = 0; x < cube_len; x += 0.1)
{
for (float y = 0; y < cube_len; y += 0.1)
{
for (float z = 0; z < cube_len; z += 0.1)
{
pcl::PointXYZ basic_point;
//沿着向量(2.5, 2.5, 2.5)平移
basic_point.x = x + 2.5;
basic_point.y = y + 2.5;
basic_point.z = z + 2.5;
cloud->points.push_back(basic_point);
}
}
}
//构造圆形平面
float R = 1;
for (float radius = 0; radius < R; radius += 0.05)
{
for (float r = 0; r < radius; r += 0.05)
{
for (float ang = 0; ang <= 360.0; ang += 5.0)
{
pcl::PointXYZ basic_point;
basic_point.x = radius * sinf(pcl::deg2rad(ang)) +3;
basic_point.y = radius * cosf(pcl::deg2rad(ang)) + 3;
basic_point.z = -3;
cloud->points.push_back(basic_point);
}
}
}
cloud->width = (int)cloud->points.size();
cloud->height = 1;
//开始KMeans聚类
KMeans kmeans;
st_pointxyz center_arr[3] = {
{0, 0, 0},
{2.5, 2.5, 2.5},
{3, 3, -3}
};
kmeans.SetInputCloud(cloud);
kmeans.SetK(3);
kmeans.InitKCenter(center_arr);
kmeans.Cluster();
kmeans.SaveFile(".", "k3");
}
执行完后可以看到生成了三个文件k3-1.pcd、k3-2.pcd、k3-3.pcd,用pcd_viewer_release.exe工具打开这三个文件得到:
可以看到聚类效果还是不错的。
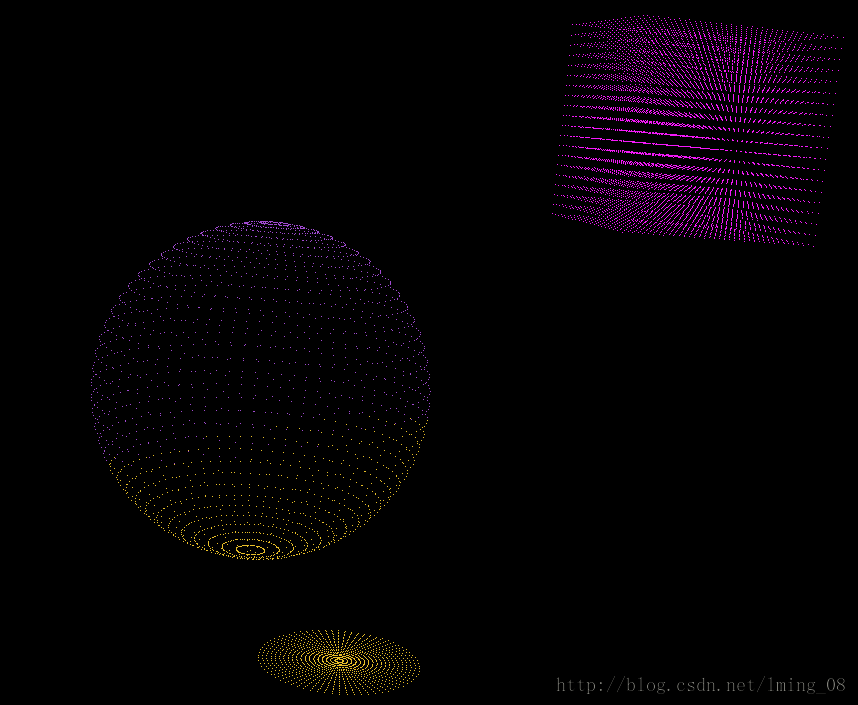
但是以上实现的K-Means聚类算法有时候效果就不是很好,例如,将上述圆的位置移到圆心为(1, 1, -3)处时,得到的效果却是这样的:
在这几天在工作中也碰到了K-Means聚类效果不太好的情况,点云为某教学楼前的一个环形路面,聚类之前的空间三维点分布情况如图所示:
选取K = 10后,聚类后的效果如下所示:
可以看到效果与期望值相差的有些离谱。
从以上两个例子中可以看到效果不太好的原因就是期望的一类A所形成的体积较大,且A类边缘点到中心的距离较大,如果其中A类的旁边(距离较近)存在另一类B且B类的体积较小,那么期望的一类A将会被分割,造成效果不好。
总之,对于具体的数据,我们要选取恰当的方法来聚类。
文章参考于:http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006910.html