机器学习理论与实战（九）回归树和模型树

       前一节的回归是一种全局回归模型，它设定了一个模型，不管是线性还是非线性的模型，然后拟合数据得到参数，现实中会有些数据很复杂，肉眼几乎看不出符合那种模型，因此构建全局的模型就有点不合适。这节介绍的树回归就是为了解决这类问题，它通过构建决策节点把数据数据切分成区域，然后局部区域进行回归拟合。先来看看分类回归树吧（CART:Classification And Regression Trees）,这个模型优点就是上面所说，可以对复杂和非线性的数据进行建模，缺点是得到的结果不容易理解。顾名思义它可以做分类也可以做回归，至于分类前面在说决策树时已经说过了，这里略过。直接通过分析回归树的代码来理解吧：

from numpy import *

def loadDataSet(fileName):      #general function to parse tab -delimited floats
    dataMat = []                #assume last column is target value
    fr = open(fileName)
    for line in fr.readlines():
        curLine = line.strip().split('\t')
        fltLine = map(float,curLine) #map all elements to float()
        dataMat.append(fltLine)
    return dataMat

def binSplitDataSet(dataSet, feature, value):
    mat0 = dataSet[nonzero(dataSet[:,feature] > value)[0],:][0]
    mat1 = dataSet[nonzero(dataSet[:,feature] <= value)[0],:][0]
    return mat0,mat1

上面两个函数，第一个函数加载样本数据，第二个函数用来指定在某个特征和维度上切分数据，示例如（图一）所示：

（图一）

       注意一下，CART是一种通过二元切分来构建树的，前面的决策树的构建是通过香农熵最小作为度量，树的节点是个离散的阈值；这里不再使用香农熵，因为我们要做回归，因此这里使用计算分割数据的方差作为度量，而树的节点也对应使用使得方差最小的某个连续数值(其实是特征值)。试想一下，如果方差越小，说明误差那个节点最能表述那块数据。下面来看看树的构建代码：

def createTree(dataSet, leafType=regLeaf, errType=regErr, ops=(1,4)):#assume dataSet is NumPy Mat so we can array filtering
    feat, val = chooseBestSplit(dataSet, leafType, errType, ops)#choose the best split
    if feat == None: return val #if the splitting hit a stop condition return val(叶子节点值)
    retTree = {}
    retTree['spInd'] = feat
    retTree['spVal'] = val
    lSet, rSet = binSplitDataSet(dataSet, feat, val)
    retTree['left'] = createTree(lSet, leafType, errType, ops)
    retTree['right'] = createTree(rSet, leafType, errType, ops)
    return retTree  

         这段代码中主要工作任务就是选择最佳分割特征，然后分割，是叶子节点就返回，不是叶子节点就递归的生成树结构。其中调用了最佳分割特征的函数：chooseBestSplit，前面决策树的构建中，这个函数里用熵来度量，这里采用误差（方差）来度量，同样先看代码：

def chooseBestSplit(dataSet, leafType=regLeaf, errType=regErr, ops=(1,4)):
    tolS = ops[0]; tolN = ops[1]
    #if all the target variables are the same value: quit and return value
    if len(set(dataSet[:,-1].T.tolist()[0])) == 1: #exit cond 1
        return None, leafType(dataSet)
    m,n = shape(dataSet)
    #the choice of the best feature is driven by Reduction in RSS error from mean
    S = errType(dataSet)
    bestS = inf; bestIndex = 0; bestValue = 0
    for featIndex in range(n-1):
        for splitVal in set(dataSet[:,featIndex]):
            mat0, mat1 = binSplitDataSet(dataSet, featIndex, splitVal)
            if (shape(mat0)[0] < tolN) or (shape(mat1)[0] < tolN): continue
            newS = errType(mat0) + errType(mat1)
            if newS < bestS: 
                bestIndex = featIndex
                bestValue = splitVal
                bestS = newS
    #if the decrease (S-bestS) is less than a threshold don't do the split
    if (S - bestS) < tolS: 
        return None, leafType(dataSet) #exit cond 2
    mat0, mat1 = binSplitDataSet(dataSet, bestIndex, bestValue)
    if (shape(mat0)[0] < tolN) or (shape(mat1)[0] < tolN):  #exit cond 3
        return None, leafType(dataSet)
    return bestIndex,bestValue#returns the best feature to split on
                              #and the value used for that split

这段代码的主干是：

遍历每个特征：

       遍历每个特征值：

               把数据集切分成两份

               计算此时的切分误差

               如果切分误差小于当前最小误差，更新最小误差值，当前切分为最佳切分

返回最佳切分的特征值和阈值

 

       尤其注意最后的返回值，因为它是构建树每个节点成分的东西。另外代码中errType=regErr 调用了regErr函数来计算方差，下面给出：

               

def regErr(dataSet):
    return var(dataSet[:,-1]) * shape(dataSet)[0]

       如果误差变化不大时（代码中(S - bestS)），则生成叶子节点，叶子节点函数是：

def regLeaf(dataSet):#returns the value used for each leaf
    return mean(dataSet[:,-1])

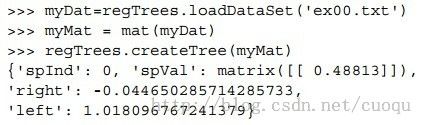
这样回归树构建的代码就初步分析完毕了，运行结果如（图二）所示：

（图二）

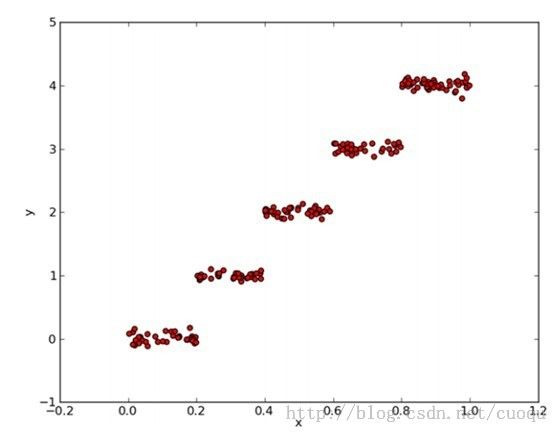
         数据ex00.txt在文章最后给出，它的分布如（图三）所示：

（图三）

       根据（图三），我们可以大概看出（图二）的代码的运行结果具有一定的合理性，选用X（用0表示）特征作为分割特征，然后左右节点各选了一个中心值来描述树回归。节点比较少，但很能说明问题，下面给出一个比较复杂数据跑出的结果，如（图四）所示：

（图四）

对应的数据如（图五）所示：

（图五）

            对于树的叶子节点和节点值的合理性，大家逐个对照（图五）来验证吧。下面简单的说下树的修剪，如果特征维度比较高，很容易发生节点过多，造成过拟合，过拟合（overfit）会出现high variance, 而欠拟合(under fit)会出现high bias,这点是题外话，因为机器学习理论一般要讲这些，当出现过拟合时，一般使用正则方法，由于回归树没有建立目标函数，因此这里解决过拟合的方法就是修剪树，简单的说就是使用少量的、关键的特征来判别，下面来看看如何修剪树：很简单，就是递归的遍历一个子树，从叶子节点开始，计算同一父节点的两个子节点合并后的误差，再计算不合并的误差，如果合并会降低误差，就把叶子节点合并。说到误差，其实前面的chooseBestSplit函数里有一句代码：

 #if the decrease (S-bestS) is less than a threshold don't do the split
    if (S - bestS) < tolS: 

         tolS 是个阈值，当误差变化不太大时，就不再分裂下去，其实也是修剪树的方法，只不过它是事前修剪，而计算合并误差的则是事后修剪。下面是其代码：

def getMean(tree):
    if isTree(tree['right']): tree['right'] = getMean(tree['right'])
    if isTree(tree['left']): tree['left'] = getMean(tree['left'])
    return (tree['left']+tree['right'])/2.0
    
def prune(tree, testData):
    if shape(testData)[0] == 0: return getMean(tree) #if we have no test data collapse the tree
    if (isTree(tree['right']) or isTree(tree['left'])):#if the branches are not trees try to prune them
        lSet, rSet = binSplitDataSet(testData, tree['spInd'], tree['spVal'])
    if isTree(tree['left']): tree['left'] = prune(tree['left'], lSet)
    if isTree(tree['right']): tree['right'] =  prune(tree['right'], rSet)
    #if they are now both leafs, see if we can merge them
    if not isTree(tree['left']) and not isTree(tree['right']):
        lSet, rSet = binSplitDataSet(testData, tree['spInd'], tree['spVal'])
        errorNoMerge = sum(power(lSet[:,-1] - tree['left'],2)) +\
            sum(power(rSet[:,-1] - tree['right'],2))
        treeMean = (tree['left']+tree['right'])/2.0
        errorMerge = sum(power(testData[:,-1] - treeMean,2))
        if errorMerge < errorNoMerge: 
            print "merging"
            return treeMean
        else: return tree
    else: return tree

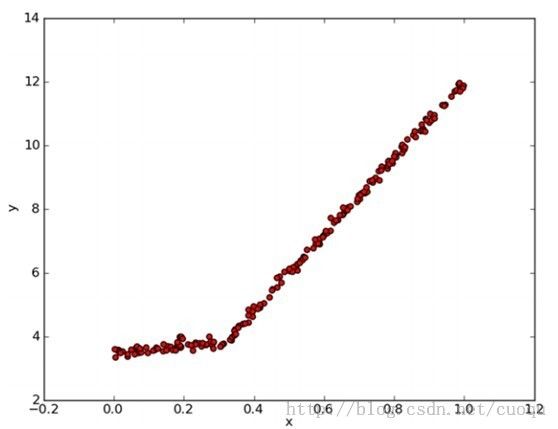
        说完了树回归，再简单的提下模型树，因为树回归每个节点是一些特征和特征值，选取的原则是根据特征方差最小。如果把叶子节点换成分段线性函数，那么就变成了模型树，如（图六）所示：

（图六）

      （图六）中明显是两个直线组成，以X坐标（0.0-0.3）和（0.3-1.0）分成的两个线段。如果我们用两个叶子节点保存两个线性回归模型，就完成了这部分数据的拟合。实现也比较简单，代码如下：

def linearSolve(dataSet):   #helper function used in two places
    m,n = shape(dataSet)
    X = mat(ones((m,n))); Y = mat(ones((m,1)))#create a copy of data with 1 in 0th postion
    X[:,1:n] = dataSet[:,0:n-1]; Y = dataSet[:,-1]#and strip out Y
    xTx = X.T*X
    if linalg.det(xTx) == 0.0:
        raise NameError('This matrix is singular, cannot do inverse,\n\
        try increasing the second value of ops')
    ws = xTx.I * (X.T * Y)
    return ws,X,Y

def modelLeaf(dataSet):#create linear model and return coeficients
    ws,X,Y = linearSolve(dataSet)
    return ws

def modelErr(dataSet):
    ws,X,Y = linearSolve(dataSet)
    yHat = X * ws
    return sum(power(Y - yHat,2))

       代码和树回归相似，只不过modelLeaf在返回叶子节点时，要完成一个线性回归，由linearSolve来完成。最后一个函数modelErr则和回归树的regErr函数起着同样的作用。

谢天谢地，这篇文章一个公式都没有出现，但同时也希望没有数学的语言，表述会清楚。

数据ex00.txt：

0.036098 0.155096

0.993349 1.077553

0.530897 0.893462

0.712386 0.564858

0.343554 -0.371700

0.098016 -0.332760

0.691115 0.834391

0.091358 0.099935

0.727098 1.000567

0.951949 0.945255

0.768596 0.760219

0.541314 0.893748

0.146366 0.034283

0.673195 0.915077

0.183510 0.184843

0.339563 0.206783

0.517921 1.493586

0.703755 1.101678

0.008307 0.069976

0.243909 -0.029467

0.306964 -0.177321

0.036492 0.408155

0.295511 0.002882

0.837522 1.229373

0.202054 -0.087744

0.919384 1.029889

0.377201 -0.243550

0.814825 1.095206

0.611270 0.982036

0.072243 -0.420983

0.410230 0.331722

0.869077 1.114825

0.620599 1.334421

0.101149 0.068834

0.820802 1.325907

0.520044 0.961983

0.488130 -0.097791

0.819823 0.835264

0.975022 0.673579

0.953112 1.064690

0.475976 -0.163707

0.273147 -0.455219

0.804586 0.924033

0.074795 -0.349692

0.625336 0.623696

0.656218 0.958506

0.834078 1.010580

0.781930 1.074488

0.009849 0.056594

0.302217 -0.148650

0.678287 0.907727

0.180506 0.103676

0.193641 -0.327589

0.343479 0.175264

0.145809 0.136979

0.996757 1.035533

0.590210 1.336661

0.238070 -0.358459

0.561362 1.070529

0.377597 0.088505

0.099142 0.025280

0.539558 1.053846

0.790240 0.533214

0.242204 0.209359

0.152324 0.132858

0.252649 -0.055613

0.895930 1.077275

0.133300 -0.223143

0.559763 1.253151

0.643665 1.024241

0.877241 0.797005

0.613765 1.621091

0.645762 1.026886

0.651376 1.315384

0.697718 1.212434

0.742527 1.087056

0.901056 1.055900

0.362314 -0.556464

0.948268 0.631862

0.000234 0.060903

0.750078 0.906291

0.325412 -0.219245

0.726828 1.017112

0.348013 0.048939

0.458121 -0.061456

0.280738 -0.228880

0.567704 0.969058

0.750918 0.748104

0.575805 0.899090

0.507940 1.107265

0.071769 -0.110946

0.553520 1.391273

0.401152 -0.121640

0.406649 -0.366317

0.652121 1.004346

0.347837 -0.153405

0.081931 -0.269756

0.821648 1.280895

0.048014 0.064496

0.130962 0.184241

0.773422 1.125943

0.789625 0.552614

0.096994 0.227167

0.625791 1.244731

0.589575 1.185812

0.323181 0.180811

0.822443 1.086648

0.360323 -0.204830

0.950153 1.022906

0.527505 0.879560

0.860049 0.717490

0.007044 0.094150

0.438367 0.034014

0.574573 1.066130

0.536689 0.867284

0.782167 0.886049

0.989888 0.744207

0.761474 1.058262

0.985425 1.227946

0.132543 -0.329372

0.346986 -0.150389

0.768784 0.899705

0.848921 1.170959

0.449280 0.069098

0.066172 0.052439

0.813719 0.706601

0.661923 0.767040

0.529491 1.022206

0.846455 0.720030

0.448656 0.026974

0.795072 0.965721

0.118156 -0.077409

0.084248 -0.019547

0.845815 0.952617

0.576946 1.234129

0.772083 1.299018

0.696648 0.845423

0.595012 1.213435

0.648675 1.287407

0.897094 1.240209

0.552990 1.036158

0.332982 0.210084

0.065615 -0.306970

0.278661 0.253628

0.773168 1.140917

0.203693 -0.064036

0.355688 -0.119399

0.988852 1.069062

0.518735 1.037179

0.514563 1.156648

0.976414 0.862911

0.919074 1.123413

0.697777 0.827805

0.928097 0.883225

0.900272 0.996871

0.344102 -0.061539

0.148049 0.204298

0.130052 -0.026167

0.302001 0.317135

0.337100 0.026332

0.314924 -0.001952

0.269681 -0.165971

0.196005 -0.048847

0.129061 0.305107

0.936783 1.026258

0.305540 -0.115991

0.683921 1.414382

0.622398 0.766330

0.902532 0.861601

0.712503 0.933490

0.590062 0.705531

0.723120 1.307248

0.188218 0.113685

0.643601 0.782552

0.520207 1.209557

0.233115 -0.348147

0.465625 -0.152940

0.884512 1.117833

0.663200 0.701634

0.268857 0.073447

0.729234 0.931956

0.429664 -0.188659

0.737189 1.200781

0.378595 -0.296094

0.930173 1.035645

0.774301 0.836763

0.273940 -0.085713

0.824442 1.082153

0.626011 0.840544

0.679390 1.307217

0.578252 0.921885

0.785541 1.165296

0.597409 0.974770

0.014083 -0.132525

0.663870 1.187129

0.552381 1.369630

0.683886 0.999985

0.210334 -0.006899

0.604529 1.212685

0.250744 0.046297

转载请注明来源：http://blog.csdn.net/cuoqu/article/details/9502711

参考文献：

      [1] machine learning in action.Peter Harrington