Ng机器学习系列补充:4、关联分析算法FP_Growth
机器学习补充系列国际权威的学术组织the IEEE International Conference on Data Mining (ICDM,国际数据哇局会议) 2006年12月评选出了数据挖掘领域的十大经典算法:C4.5, k-Means, SVM, Apriori, EM, PageRank, AdaBoost, kNN, Naive Bayes, and CART,它们在数据挖掘领域都产生了极为深远的影响,这里对他们做一个简单介绍,仅作为对Ng机器学习教程的补充。
由于k-Means、SVM、EM、kNN、Naive Bayes在Ng的系列教程中都有涉及,所以此系列教程只涉及决策树算法C4.5、关联规则算法Apriori、网页排名算法PageRank、集成学习算法AdaBoost(Adaptive Boosting,自适应推进)、分类与回归树算法CART(Classification and Regression Trees);另外会加上对神经网络的BP算法介绍,后续也会考虑介绍遗传算法等内容。
1)FP_Growth算法核心概念
2)实例演示FP_Tree的构造
3)挖掘FP_Tree
4)另一个例子
1)FP_Growth算法核心概念
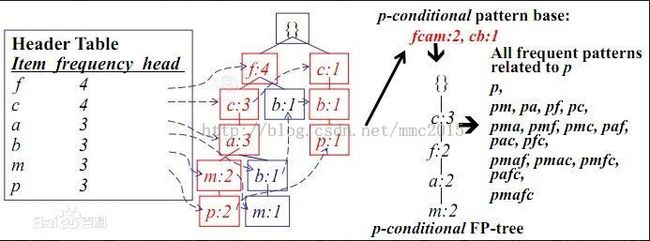
FP_Growth(FrequentPattern,频繁模式)算法是对Apriori算法的补充,是为了克服Apriori算法生成大量候选项集和多次扫描数据库的缺点。FP_Gwoth算法是一种不生成候选项集从而寻找频繁项集的算法,主要基于树结构:包含一棵FP_Tree和一个项头表,项头表中的每一项通过一个结点链指向它在树中出现的位置需要注意的是项头表需要按照支持度递减排序,在FP_Tree(有后缀的也称条件FP_Tree)中高支持度的节点只能是低支持度节点的祖先节点。这样一来可以保证尽可能的共用祖先节点,更重要的是保证正确性。FP_Tree基本结构如下所示:
| //FP-tree的存储结构 typedef struct CSNode{ int item; //商品ID int count;//次数 CSNode *parent,*firstchild,*nextsibling;//父节点,孩子节点,兄弟节点 CSNode *pre,*next;//相同商品的前驱、后继节点,将相同商品的节点连接起来,根节点的直接孩子节点的这两个指针都是空 }*CSTree; |
2)实例演示FP_Tree的构造
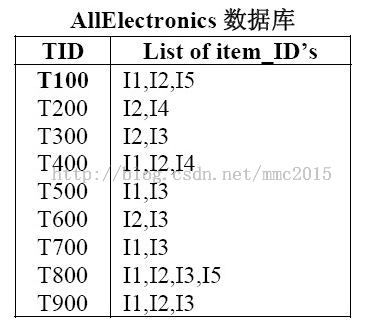
原始交易记录如下(和之前的一样):
每一行表示一条交易,共有9笔交易,左边表示交易ID,右边表示商品ID。假设在我们的问题中,最小支持度是22%,那么每件商品至少要出现9*22%=2次才算频繁。
第一次扫描数据库,统计每件商品出现的次数,按次数对各个商品递减排序,有:【I2:7, I1:6, I3:6, I4:2, I5:2】。
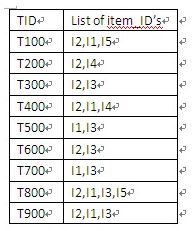
第二次扫描数据库,在每条交易中按此种顺序给商品排序,如果某个商品出现的次数小于阈值2,则删除该商品,有:
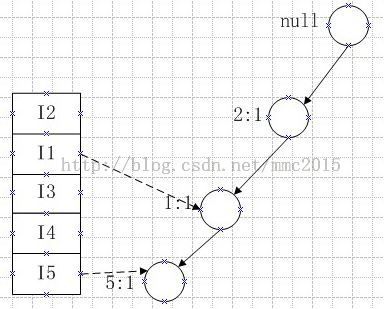
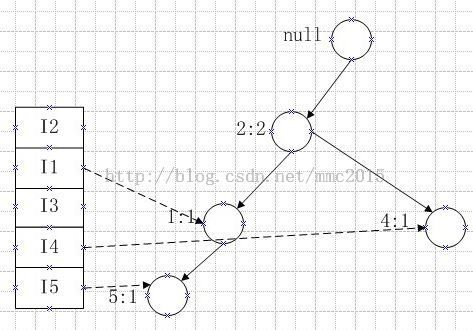
第三次访问数据库,构造FP_Tree。第一条记录:I2,I1,I5,有:
父节点没有表示出来,根节点是空节点。2:1表示商品2出现了1次,其他表示类推。左边的数组按照商品出现次数递减排列,保存了各个商品的当前指针,目的是为了在后面找到相同的后缀,将相同的商品用单项箭头虚线连起来,实际是双向链表链接的,并且将此时的节点商品1和节点商品5保存为商品1和商品5的当前指针,而对于商品2,商品3,商品4的当前指针还在左边的数组中保存。注意根节点的直接孩子不用连起来,后面会讲理由(其实根节点也可以连,看你怎么用了)。
第二条记录:I2,I4,有:
该记录和第一条记录共用前缀I2,所以商品2的次数要加1,而商品4则作为商品2的一个新孩子节点,这里没有把兄弟节点画出来。并且左边商品4要指向该节点,此时商品4的当前指针指向节点商品4。
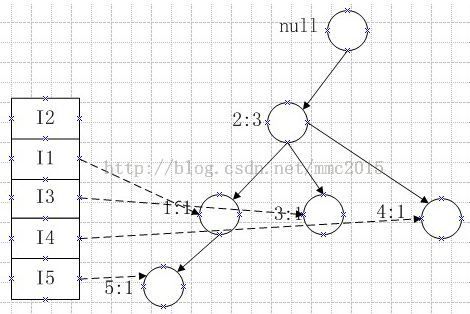
第三条记录:I2,I3,类似,结果是:
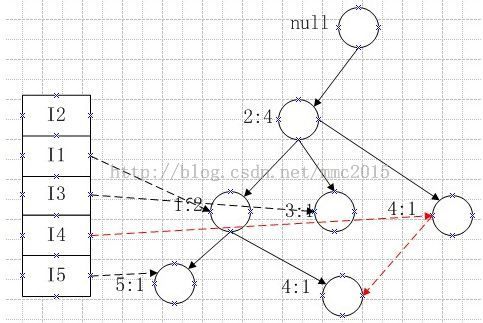
第四条记录:I2,I1,I4,有:
当添加完商品4后,商品4的当前指针要指向新的节点商品4,此时两条红色的虚线就把以商品4为后缀的节点连起来了。
第5条记录:I1,I3,有:
商品1由于和根节点的所有直接子孩子(这里只有商品2这个子孩子)不同,因此要另外开辟一条路径。商品3的当前指针要指向新的节点商品3,如图中的黄色虚线所指,到这里体现了构造FP_Tree的一般性了。
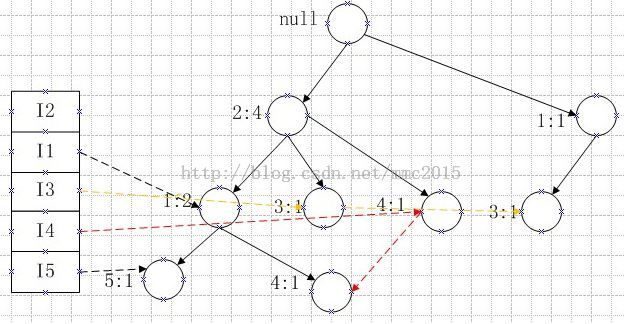
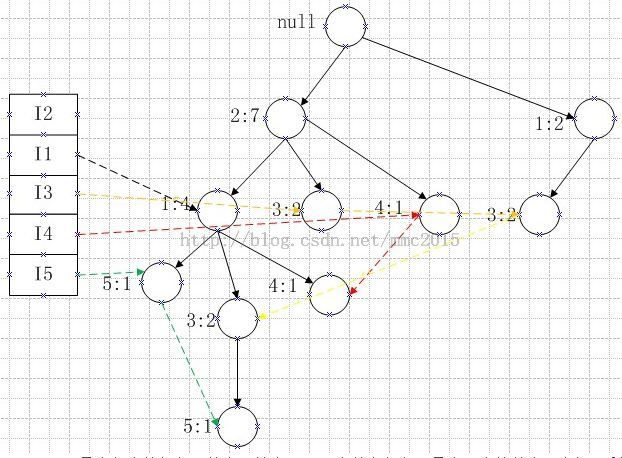
再把剩下的记录都加进来,最终的FP_Tree是:
这颗FP_Tree最大程度的把相同的商品放在用同一个节点保存,最大限度的节省了空间。剩下的工作就是挖掘这颗FP_Tree了。
3)挖掘FP_Tree
挖掘的目的是找出FP_Tree的各个路径中相同的集合,有两种方式,方式一,从根节点朝叶子节点顺着遍历树,方式二,从叶子节点朝根节点逆着遍历树。想想方式一挺麻烦的,幸亏我们设置了*parent指针,通过它就可以很方便的用方式二。
我们从商品出现次数由少到多的顺序开始遍历树,先从商品5开始,由于有*pre,*next指针分方便将所有以商品5做为叶子节点的路径全找出来,然后再根据*parent指针找到父节点,根节点是空不用找。以I5做元素的条件模式基是:{(I2 I1:1),(I2 I1 I3:1)}。后面的1表示出现商品I2,I1,I5同时出现的次数。现在解释为什么:根节点的直接孩子不用*pre,*next指针连起来,因为假如连起来的话,那么以它为后缀时,将没有前缀,也就是说它的频繁项集是1,这在大多数情况下没意义。由它构造出条件FP_tree,注意由于开始按照商品名称排序了,那么条件模式基中的每一项也会按照这种方式排序。如果条件模式基中某项A是另外一项B的子集那么在算B时,要将A出现的次数加上,实现这个功能最简单明了的方法就是一一匹配,假如条件模式基共有N项,则时间复杂度是N的平方,若先按照条件模式基的长度递增排序得到:{(I2 I1:1),(I2 I1 I3:1)},排序的时间复杂度是N*log(N),那么只有可能是长度短的项是长度长的项的子集,此时总匹配次数是:N-1 + N-2 + ,,, + 1 = N*(N-1)/2,和前面的排序时间加起来是:N*log(N) + N*(N-1)/2当N大于时4时,该值小于N的平方。在实际中N一般会大于4。最终我们得到以I5作为后缀的频繁项集是:{I2 I5:2},{I1 I5:2},{I2 I1 I5:2}他们出现的次数都大于等于最小支持度。类似可以得到其它后缀的频繁项集。
FP_Growth算法不产生候选序列,并且只需要3次遍历数据库,对比Apriori算法而言有了很大的改进。
4)另一个例子
参考:
http://blog.sina.com.cn/s/blog_6e85bf420100ogp8.html
http://blog.csdn.net/xiaofengcanyuexj/article/details/41656335
http://baike.baidu.com/view/3342544.htm