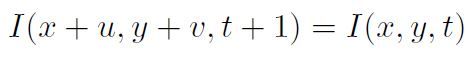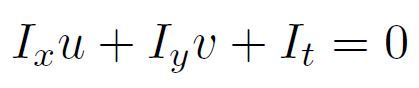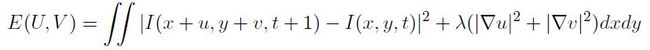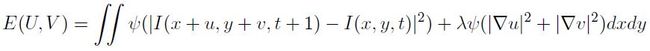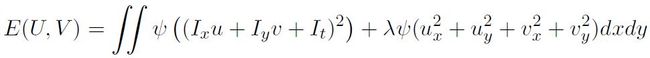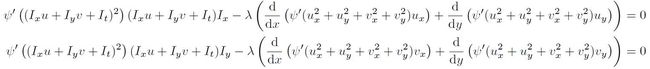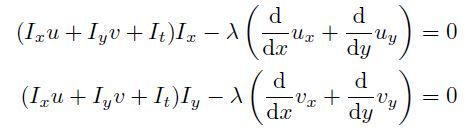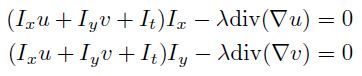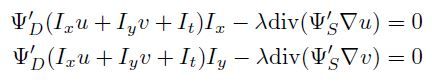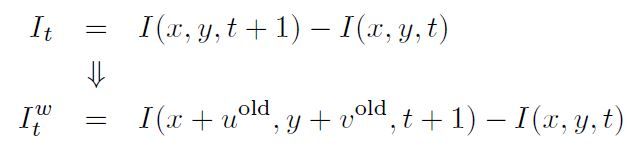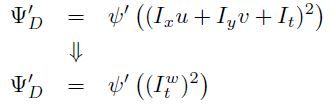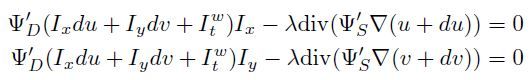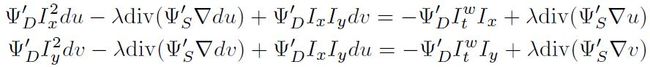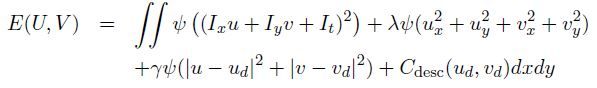图像处理中的全局优化技术(Global optimization techniques in image processing and computer vision) (三)
MulinB按:最近打算好好学习一下几种图像处理和计算机视觉中常用的 global optimization (或 energy minimization) 方法,这里总结一下学习心得。分为以下几篇:
1. Discrete Optimization: Graph Cuts and Belief Propagation
2. Quadratic Optimization : Poisson Equation and Laplacian Matrix
3. Variational Methods for Optical Flow Estimation (本篇)
4. TODO: Likelihood Maximization (e.g., Blind Deconvolution)
3. Variational Methods for Optical Flow Estimation
Optical Flow(光流法)这个词乍一看很能唬住人,啥东东这么高级,是追踪光的流动轨迹吗?没这么玄乎。其实optical flow是一个很朴实的low-level vision的东西,就是每个pixel从一帧图像到另一帧图像的位置偏移(displacement)。如下图所示,
Two Input Frames Optical Flow (Vector Plot) Optical Flow (Color Plot)
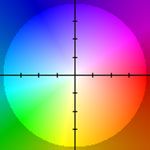
上面的color plot,其实是通过一个二维的color wheel将2D的motion vector用颜色show出来,常用的color wheel如下所示(中心点表示横向和纵向的位移都为0,用白色表示):
在上面的例子中,可以看出背景中大多数pixel是往左上方偏移一点(相对于镜头),因此在optical flow中,背景呈现浅蓝色(在color wheel的第二象限)。至于计算optical flow这个东东到底有啥用途,可以说绝对是视频编辑的基石,参见这里(Art of Optical Flow,被墙的可以参看这里的英文原版)有一篇有趣的介绍optical flow在电影编辑中的作用(比如合成《黑客帝国》中的超级慢镜头)。
正是由于其重要的作用,如何计算optical flow从1980s就开始成为计算机视觉的研究热门。早期的计算主要focus在计算subpixel级的displacement,随着视频分辨率的增加,最近的很多算法开始考虑较大的displacement,通常需要先计算帧与帧之间pixel级别的correspondence,然后进行warping后再使用传统算法计算subpixel精度的optical flow结果。至于评测optical flow算法的accuracy,最经典的一个benchmark是Middlebury,但其用于排名的dataset只有12张图,比较容易overfitting,最近两年又出现两个比较popular的benchmark,Sintel和KITTI。
3.1 Classic Framework
我们先从optical flow算法的目的说起。令I(x,y,t)表示在t时刻frame上像素(x,y)处的亮度(或颜色),那么optical flow的目的就是求出在t+1时刻的frame上,该像素相对于原来(x,y)的位移量(u,v),用方程表示即:
其中u和v是未知量。这就是optical flow中著名的Brightness Constancy Model。
不过,数字图像毕竟是离散化pixel by pixel的,如果只给出两帧图像,如何计算出每个pixel的subpixel级的displacement(位移)呢?如果从correspondence的角度去考虑,在frame1中的某个pixel,只能找到其在frame2中对应的pixel整数位置,这样只能得到pixel级的displacement,而无法精确到subpixel精度。在经典的optical flow算法中,一般利用一阶泰勒展开作为工具来建立图像gradient和displacement之间的关系,这一步骤通常被称为Linearization。具体原理如下(这里有个不错的tutorial介绍的也很详细,by David Fleet and Yair Weiss):
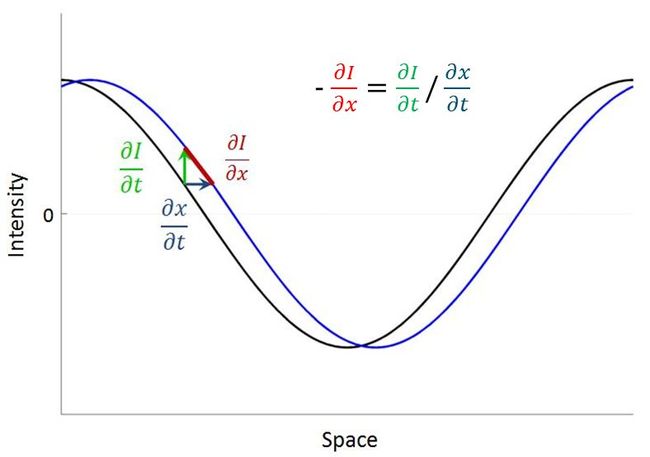
假设图像的intensity是连续的,如下图所示(1D case),黑色的曲线表示frame1中的图像,蓝色的曲线表示frame2中的图像,待求的displacement是深蓝色的箭头dx/dt。对曲线进行一阶泰勒展开,其实就是假设曲线的局部是线性的,这样可以考察如图的红绿蓝组成的三角形。注意,dI/dx并非是红色线段的长度,而是其斜率。这样可以得到图中所示的关系,注意负号是因为斜率其实表示的是钝角的tan。这样一来就建立了图像的derivative和displacement之间的关系,注意dI/dx是图像在spatial上的derivative,dI/dt是图像在temporal上的derivative。
将上面的这个方程用在2D的图像上,对于每个pixel,可以写出以下方程:
其中,I_x和I_y是图像沿spatial的x和y两个方向的derivative(即图像gradient的两个分量),I_t是图像沿temporal的derivative(可以用两帧图像的difference来近似),u和v是该pixel沿x和y方向的位移,也就是待求的optical flow未知量。这其实就是对上面的Brightness Constancy Model的Lineariazation的结果,也就是optical flow中著名的Gradient Constraint Equation。
需要注意的是,上面这个模型是建立在两个假设基础上:第一,图像变化是连续的;第二,位移不是很大。如果这两点假设不成立,那么泰勒展开的近似是很差的。直觉想象一下,如果图像不是连续的,而且displacement很大,无论如何是无法将displacement和图像gradient联系起来的。不过在实际中,上述两个假设可以很容易使其成立。关于第一点,一般可以预先对图像进行Gaussian Smoothing,使其变化较为平缓;关于第二点,一般是对图像降分辨率建立金字塔,通过Coarse-To-Fine的方式一步一步去求解。
基于上面的方程,最经典的两个optical flow算法,Lucas-Kanade方法[1]和Horn-Schunck方法[2],分别从不同的角度增加了求解该方程的稳定性。Lucas-Kanade方法是将每个pixel周围的一些pixels考虑进来,但每个pixel的未知量是单独求解的,所以是一种local方法;而Horn-Schunck方法是将上面的方程纳入到一个regularization的framework中,加入optical flow是locally smooth的prior,所有的pixel的未知量之间相互依赖,需要用global optimization的方法求解。目前state-of-the-art的方法,一般都是基于Horn-Schunck的framework做的,这里要介绍的经典optical flow算法也是基于这个framework经过几次改良得到的。
石器时代:令小写的u和v分别表示每个pixel处沿x和y方向的displacement,大写的U和V分别表示由所有pixel的u和v组成的map,那么Horn-Schunck的目标函数可以写作如下形式:
可以看出,第一项data term其实就是Brightness Constancy Model的Least Square形式,第二项regularization term目的是令结果的U和V较为smooth。对该目标函数进行minimization即可求出U和V。由于该目标函数是quadratic,根据calculus of variation(变分法)中的 Euler-Lagrange Equation (two unknown function -- U and V, two variables -- x and y) 可以将其转化为偏微分方程形式,再进行离散化,最终可以归结为求解一个大型线性方程组,利用Conjugate Gradient或者SOR可以很容易求解,参见上一篇文章。
青铜时代:根据robust statistics理论,quadratic的目标函数对outlier太敏感。而其实在locally smooth assumption下,最理想的情况是一个场景中只有一种motion。如果有多种motion,那么就相互构成outlier,会严重影响结果,这显然是quadratic目标函数的软肋。而这种情况恰恰是现实中最常发生的。因此,Michael J. Black和P. Anandan [3] 提出了将上述目标函数中的L2 norm换成更为robust的函数(比如L1 norm或者truncated L1 norm),形成了目前较为常用的形式:
目前最常用的robust函数是Charbonnier函数psi(x^2)=sqrt(x^2+1e-6),即L1 norm (增加了一个很小的数字1e-6为了使其convex,容易求解optimization)。这样一来,data term是L1 norm,regularization term使用了L1 norm后其实就成了Total Variation,因此这个目标函数又被称为TV-L1 formulation。另外,目前流行的coarse-to-fine、warping的framework也是在这篇paper里基本定形的。
白银时代:为了避免光照对Brightness Constancy Model的影响,Thomas Brox等人[4] 提出在data term里引入Gradient Constancy Model(不妨看做在原来的3个color channel之外多加两个gradient channel),大大提高了算法的精确度。值得一提的是,这篇paper里提到的fixed point iteration解法(这里有Ce Liu的C++ code)比之前的graduated non-convexity算法(这里有Deqing Sun的Matlab code)貌似速度要快不少(或许是implementation的区别)。
另外值得一提的是,在Middlebury上有个叫improved TV-L1[6] 的算法,速度貌似很快,效果也不错。其实之前的很多算法都是基于TV-L1 formulation的,不过这篇paper [6] 主要是介绍一种快速算法的。其实,该文的主要contribution在于:第一,该文提出用texture decomposition的方式先提取image的texture,然后用texture作为data term,旨在避免光照等的影响,跟前面的加入gradient data term思路类似。第二,该文提出对每一个iteration求解出的flow进行median filter去掉outlier,后来这个小trick被证实是很有效的一步 [7]。另外,该文 [6] 中对implementation的描述也比较细致,如果要实现optical flow算法,这篇paper很值得一看(可以直接忽略其之前的版本[5])。
黄金时代:对经典算法中使用的各种trick进行总结的集大成者是Deqing Sun等人的CVPR 2010 paper [7]及其扩展IJCV 2013 paper [8]。该猛人将之前paper中五花八门的trick统统试了一遍,总结出哪些是精华,哪些是糟粕。最难能可贵的是,他将所有的matlab代码公布于众,使得后来者省去了不少揣测如何做implementation的时间,强赞一个。美中不足的是,这些实验是在Middlebury的training data上完成的,但是Middlebury的dataset有点小,只有几张图,难免让人觉得有可能overfitting,调查的trick是否真的如paper中得出的结论那般,值得商榷(在其IJCV 2013 paper [8]中也发现,算法在KITTI的benchmark上和在Middlebury上performance很不一样)。
3.2 Algorithm and Implementation Details
这里简单地对求解上述framework的算法理一理,主要参考Thomas Brox的paper [4] 以及Ce Liu的Implementation及他对Brox算法的重新推导[9](Appendix A)。为了简化推导过程,下面假设图像I是由3个color channel加上2个gradient channel组成的5个channel的图像(paper [4]中推导时将gradient channel显式的表示了出来,看起来过于复杂)。由上面的TV-L1 formulation,经过Linearization后,目标函数如下所示(下标表示偏导):
根据calculus of variation(变分法)中的 Euler-Lagrange Equation (two unknown function -- U and V, two variables -- x and y) ,可以得到以下两个偏微分方程:
这个方程有点麻烦,主要是因为robust函数psi引入的non-linearity。我们不妨先考虑没有psi时的情况,即Horn-Schunck的quadratic目标函数,这时上述偏微分方程很简单:
用divergence运算符及gradient运算符表示,即为:
注意这两个方程是对于每个pixel建立的,其中u和v是未知量,如果将divergence和gradient离散化(见上一篇中的基础介绍),可以表示成当前点未知量uv与周围几个pixel未知量uv之间的线性关系。这样以来,相当于每个pixel可以列出2个线性方程,假设图像一共有N个pixel,那么一共可以建立2N个线性方程,未知量也是2N个,由于每个pixel与周围一些pixel存在依赖关系,这2N个方程组成的方程组需要联立求解。于是归结为求解一个大型稀疏线性方程组的问题(参见上一篇文章),较为简单,可以用Conjugate Gradient或SOR求解。
回到上面那个复杂点的nonlinear偏微分方程,一个简单而有效的方法来消除non-linearity是,将nonlinear factor看做已知,用上一次迭代的未知量直接代入计算!这样多迭代几次,如果算法可以收敛,最终求出的未知量是可以满足整个nonlinear方程的!这就是fixed point iteration算法,一个可以化复杂为简单的有效算法。注意,每一次迭代其实都需要求解上述的线性方程组,在实际应用中,一般固定迭代次数(5~10次)即可。如果用大写Psi'_D表示上面方程中data term中的nonlinear factor,用大写Psi'_S表示smooth term中的nonlinear factor,那么复杂的方程可以简化为如下形式:
由于Psi'_D和Psi'_S可以直接使用上一次迭代的结果进行计算,该方程和上面的linear system解法一样。
更进一步,由于Linearization在u和v比较小时才比较精确,为了提高精度,在上面的迭代中,可以用上一个迭代的uv结果对第二帧图像进行warp,用warp之后的图像代替原来的第二帧图像,这样每次求的未知量uv其实只是增量,一般用du和dv表示,每次迭代将其累加到uv的结果上即可得到最终结果。具体来讲,上面的方程中涉及到第二帧图像的主要是I_t,将其用warp之后的第二帧图像计算,即作以下替换:
注意由于u和v是float point类型,上面的warp过程中一般需要进行插值计算,可以用bilinear或者bicubic插值算法。另外要注意的是,Psi'_D中也包含I_t项,如果也将其替换,那么需要作以下调整(不需要再考虑u和v):
这样一来,方程就变为:
其中u和v用上一次iteration的结果,只有du和dv是未知量。注意,divergence和gradient operator离散化后其实是线性运算符,所以sooth term可以进行分离,整理后可以得到:
注意这两个方程是对于每个pixel建立的,等式左侧的du和dv是未知量,右侧是已知量(可以用上一个迭代的结果计算)。等式左侧含有divergence和gradient operator的项其实耦合了每个pixel与周围pixel的关系,这是regularization的功能所在。像上面介绍的一样,将该方程离散化后,可以建立2N个线性方程,联立可以求得每个pixel的du和dv。
另外,这个求解过程一般从图像金字塔上coarse-to-fine地进行,从最coarse的level开始,每个level计算完成再迁移到下一个level,使用上一个level的uv结果进行初始化。总之,整个算法可以简单的描述为以下流程(具体参见Ce Liu的C++ code):
在Thomas Brox和牛魔王Jitendra Malik近来的一篇TPAMI paper [10]里,提出将descriptor matching融合到optical flow的framework中,增加其对一些小的object的motion捕捉(这种小的object在之前的coarse-to-fine的方法中一般会丢失)。主要思想是增加一对辅助未知量u_d,v_d,将descriptor matching的cost和之前的cost function关联起来,这时的variational framework目标函数变为:
其中C_desc是descriptor matching的cost。辅助变量u_d和v_d的作用是可以将该目标函数decouple成两个子问题:descriptor matching和variational求解。迭代计算这两个子问题即可求得最终结果,比如,先descriptor matching得到u_d和v_d,然后再用上述variational framework计算,然后再descriptor matching,然后再variational framework…
该integrated framework其实在benchmark上成绩并不突出,只是后来基于此framework做的DeepFlow(ICCV 2013 oral paper),效果亮瞎了(见Sintel和KITTI benchmark),值得期待(目前paper还没放出)。
[1] B.D. Lucas and T. Kanade, “An Iterative Image Registration Technique with an Application to Stereo Vision,” IJCAI, 1981.
[2] B.K.P. Horn and B.G. Schunck, “Determining Optical Flow,” Artificial Intelligence, 1981.
[3] M.J. Black and P. Anandan, “The Robust Estimation of Multiple Motions: Parametric and Piecewise-Smooth Flow Fields,” CVIU, 1996.
[5] C. Zach, T. Pock, and H. Bischof, “A Duality Based Approach for Realtime TV-L1 Optical Flow,” DAGM, 2007.
[6] A. Wedel, T. Pock, C. Zach, H. Bischof, and D. Cremers, “An Improved Algorithm for TV-L1 Optical Flow Computation,”Dagstuhl Motion Workshop, 2008.
[7] D. Sun, S. Roth, and M.J. Black, “Secrets of Optical Flow Estimation and Their Principles,” CVPR, 2010.
[8] D. Sun, S. Roth, and M.J. Black, “A Quantitative Analysis of Current Practices in Optical Flow Estimation and the Principles Behind Them,” IJCV, 2013.
[9] C. Liu, “Beyond Pixels: Exploring New Representations and Applications for Motion Analysis,” PhD Thesis, MIT, 2009.
[10] T. Brox and J. Malik, “Large Displacement Optical Flow: Descriptor Matching in Variational Motion Estimation,” TPAMI, 2011.