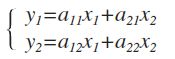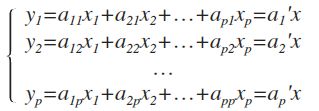数据科学之机器学习15: 主成分分析

图片为：本文实例数据得到的，前两个主成分的散点图！

“文章原创，转载请注明出处”

在之前线性回归3提到多重共线性问题，当时说了一些解决这个问题的办法，其中一种就是今天要说的主成分分析。

主成分分析，Principal Components Analysis，简称PCA，是变量选择的一种方法。其一般的目的就是：变量的降维和主成分的解释！当主成分用于聚类或者回归，这个时候就是在做变量的降维；而当用来分析变量，尤其是使用前两个主成分进行散点图的绘制时，此时就是在对变量利用主成分做出一些解释。在了解主成分分析的原理之后，相信对这两个目的就可以很容易直观的理解了！

一、原理初窥

在用数学公式和概率统计知识推导其原理之前，不妨先直观地看看主成分分析到底是要干嘛，以及大致是怎么干的！

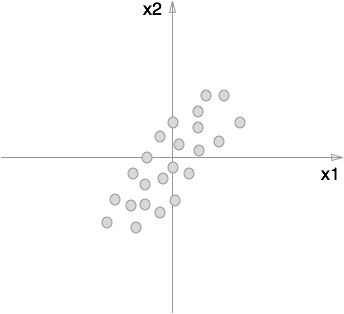
我们就用两个变量来说这个问题，变量分别记作 x1,x2 。那么，我们先画个散点图吧，也许它们的散点图是这个样子的：

我们可以看到，这两个变量明显呈现一种线性关系，如果在做线性回归时，将这两个变量都用作自变量，然后对某一个因变量进行线性拟合，那必定会存在一些问题。那么主成分分析是要做什么呢？其实主成分分析就是要寻找变量 y1,y2 去替代 x1,x2 ，而且满足 y1,y2 几乎不相关，同时 y1,y2 能够保留 x1,x2 所包含的信息。

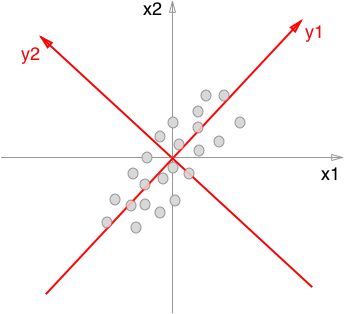
那么主成分分析是如何做的呢？这个时候就需要考虑旋转坐标轴，当我们像下图那样旋转过坐标轴之后，上面提出的要求就得到了实现。

从这张图我们就可以看出，数据投影到 y1,y2 两轴后，数据基本不相关，而且在 y1 轴就保留了原本数据的大部分信息， y2 保留了数据的另外一部分信息。由此可见，数据越是集中在 y1 轴两侧，数据映射到 y1 轴后保留的信息就越多，而 y2 就越少。当 y2 含有的信息非常少，少到接近于0时，那么此时就到达了变量选择的目的，因为此时只要保留 y1 就可以了。

二、原理

我们将数据映射到 y1,y2 轴，其实就是将原数据做个线性变换。利用上面的内容举个简单地例子就是：

其中的系数满足： a211+a221=1,a212+a222=1 。这样就可以成功地将数据投影到 y1,y2 轴。这里我们考虑更一般的情况，考虑 p 维的情况：

其中 ai=(a1i,a2i,…,api)′,i=1,2,…,p ，且满足 a′ia1=1 。

下面要考虑的就是，如何选择 a1 ，使得 V(y1) 到达最大，找到之后， y1 就是第一主成分。

首先， V(y1)=a′1Σa1 ，其中 Σ=V(x) 为协方差矩阵。我们知道 Σ 是非负定的，那么其所有的特征值必定都是大于等于0的，我们可以排个序： λ1⩾λ2⩾⋯⩾λp⩾0 ，其对应的特征向量记为： t1,t2,…,tp ，显然这些特征向量是相互正交的。记 T=(t1,t2,…,tp)=(tik),Λ=diag(λ1,λ2,…,λp) 。

那么根据谱分解就有： Σ=TΛT′=∑pi=1λitit′i 。那么带入到 V(y1) 中就有：

V(y1)=∑i=1pλia′1tit′ia1=∑i=1pλi(a′1ti)2

由于特征值中 λ1 是最大的，那么就有：

V(y1)⩽λ1∑i=1p(a′1ti)2=λ1∑i=1pa′1tit′ia1=λ1a′1TT′a1=λ1

可以看到最终的结果是： V(y1)⩽λ1 。那么什么时候取等号呢？取 a1=t1 ，则有：

t′1Σt1=t′1(λ1t1)=λ1

到止为止，就可以看到。当 y1=t′1x 时就有其 V(y1) 达到最大，为 λ1 。那么此时 y1=t′1x 就是该数据第一主成分。

同理可以求解第二主成分直至最后。但是，在求解第二第三主成分的时候，需要注意一个新的问题：主成分之间不相关，即 Cov(yi,yk)=0,i≠k ，如何证明非常简单，我就不说了，自己动动手吧。

三、具体实例

我们使用R语言来做个小例子：

1 2 3 4 5 6 7 8 9 10 11 12

# 构造一个数据集 set.seed(10) x1 <- seq(1, 50, 2) + rnorm(25, mean=1, sd=1) x2 <- 2*x1 + rnorm(25, mean=1, sd=1) x3 <- x1/2 + x2 + rnorm(25, mean=1, sd=1) x <- data.frame(x1=x1, x2=x2, x3=x3) # 计算协方差矩阵 Sig <- cov(x) # 计算特征值和特征向量 eigen(Sig)

得到结果如下：

1 2 3 4 5 6 7 8

$values [1] 2381.3724526 0.3681085 0.1165201 $vectors [,1] [,2] [,3] [1,] -0.2982259 -0.4601189 0.83627265 [2,] -0.6002191 -0.5908325 -0.53912331 [3,] -0.7421579 0.6627273 0.09997061

得到了特征值为： λ1=238.372,λ2=0.368,λ3=0.11652 ，可以看到第一主成分 y1=t′1x=−0.298x1−0.600x2−0.742x3 的特征值 λ1 的值远大于其余的(由于数据构造时就是以 x1 为底的)。说明第一主成分能够解释数据的大部分信息，那么如何衡量呢？

这时候就需要使用到贡献率这个概念，某一个主成分 yi 的贡献率定义为： λi∑pi=1λi 。

贡献率越大说明这个主成分能够解释数据的信息就越多，在具体的问题中，还常常用到一个概念，就是累积贡献率。前 k 个主成分的累计贡献率就是： ∑ki=1λi∑pi=1λi 。实际中，当前 k 个主成分的累积贡献率达到某个临界值，比如 80% ，就选择前 k 个主成分进行下一步操作(比如说聚类，回归或者单纯地做分析等等)

四、基于相关矩阵

考虑这样两种情况：各个变量的单位不全相同，也就是数据的量纲不同；各变量之间的单位相同，但是变量的方差较大，也就是数值大小相差较大。那么这个时候，如果从协方差矩阵出发求解主成分，就显得不大合适了。

在之前的文章中提到过，当所有的变量都进行了标准化之后，协方差矩阵 Σ 就转换成了相关矩阵 R ！

那么，剩下的求解过程就与上面相同了，这里不再叙述。需要指出的是，标准化与否，所得到的结果可能会有很大的不同，所以，判断一批数据是否需要标准化是很有必要的！

五、R语言实现

主成分分析的R语言实现比较简单，可以直接使用eigen()函数求出特征值特征向量。当然也有自带的函数：princomp()以及psych包中的principal()函数，可以自己查找一下帮助文档，这里就不做介绍了

转自：http://jackycode.github.io/blog/2014/05/11/principal-components/