图

图的定义和术语

图中数据元素通常称为顶点(Vertex),V是顶点的有穷非空集合

VR是两个顶点之间的关系的集合

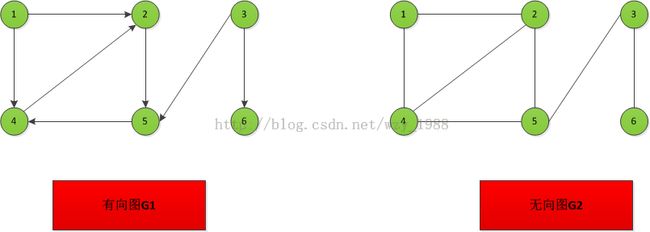
1. 若<v,w>属于VR,则<v,w>表示从v到w的一条弧(Arc),且称v为弧尾(Tail)或起始点(Inital node),称w为弧头(Head)或终端点(Terminal node),此图称为有向图(Digraph)
   
2. 若<v,w>属于VR必有<w,v>属于VR，即VR是对称的，则以无序对(v,w)代替这两个有序对，表示v和w之间的一条边(Edge),此时图称为无向图(Undigraph)
   
   

我们用n表示图中顶点的数目，用e表示边或弧的数目，那么

1. 对于无向图，e的取值范围是0到1/2*n*(n-1).有1/2*n*(n-1)条边的无向图称为完全图(completed graph)
2. 对于有向图，e的取值范围是0到n*(n-1).具有n(n-1)条弧的有向图称为有向完全图。有很少条边或弧的图称为稀疏图(sparse graph)，反之，称为稠密图(dense graph)
   
   

对于无向图，G=(V, {E})：

• 如果边(v,v')属于E，则称顶点v和v‘互为邻接点，即v和v'相邻接
• 边(v,v')依附于顶点v和v’，或者说(v,v')和顶点v和v‘相关联
• 顶点v的度(degree)是和v相关联的边的数目，记为TD(v)

对于有向图，G=(V,{A})：

• 如果弧<v,v'>属于A,则称顶点v邻接到顶点v‘，顶点v’邻接自顶点v。弧<v,v'>和顶点v，v'相关联
• 以顶点v为头的弧的数目称为v的入度(indegree),记为ID(v)
• 以v为尾的弧的数目称为v的出度(outdegree),记为OD(v).顶点v的度记为TD(v) = ID(v)+OD(v)

在无向图G中：

• 如果顶点v到顶点v‘有路径，则称v和v’是连通的
• 如果对于图中任意两个顶点vi，vj属于V，vi和vj都是连通的，则称G是连通图(Connected Graph)
• 连通分量(Connected Component),无向图中的极大连通子图

在有向图G中：

• 如果对于每一对vi，vj属于V，并且vi != vj，从vi到vj和从vj到vi都存在路径，则称G是强连通图
• 有向图的极大强连通子图称作有向图的强连通分量

图的存储结构

之前照着<<数据结构>>抄了部分图的存储结构定义,真是在acm平台做题的时候发现书上的东西基本作用不大,用n * n的邻接矩阵足可以解决大部分问题

邻接矩阵

n个顶点的图,可用n * n的邻接矩阵来表示,其中(n1, n2 )联通则为1,不联通则为0

上述有向图G1的邻接矩阵为:

int graph[6][6] = 
{
	{0, 1, 0, 1, 0, 0},
	{0, 0, 0, 0, 1, 0},
	{0, 0, 0, 0, 1, 1},
	{0, 1, 0, 0, 0, 0},
	{0, 0, 0, 1, 0, 0},
	{0, 0, 0, 0, 0, 0},
};

 

图的遍历

图的遍历分为广度优先遍历(breadth-first-search)和深度优先遍历(depth-first-search)

广度优先遍历

广度优先搜索是很多重要的图算法的原型。在prime最小生成树和Dijkstra单源最短路径算法中，都采用了与广度优先搜索类似的思想

在给定图G=（V,E）和一个特定的源顶点s的情况下，广度优先搜索系统地探索G的边，以期“发现”可从s到达的所有顶点，并计算s到所有这些可达顶点之间的距离（即最小的边数）。BFS同时还能生成一颗根为s，且包括所有s的可达顶点的广度优先树。对从s可达的任意顶点v，广度优先树中从s到v的路径对应于图G中从s到v的一条最短路径，即包含最少边数的路径。BFS之所以 称之为广度优先搜索，是因为，它自始至终都是从一个结点沿其广度方向向外扩展。BFS算法自始至终一直通过已找到和未找到顶点之间的边界向外扩展，就是说，算法首先搜索和s距离为k的所有顶点，然后再去搜索和s距离为k+1的其他顶点

为了记录搜索的轨迹，广度优先搜索将每个顶点都着色为白色，灰色或黑色。算法开始前，所有的顶点都是白色;随着搜索的进行，各顶点会逐渐变成灰色，然后成为黑色。在搜索中第一次碰到一个顶点时，称该顶点被发现了，此时该顶点变为非白色。因此，灰色和黑色顶点都是已被发现的，但是广度优先搜索还是对它们加以区分，以确保搜索是以一种广度优先的顺序进行的。若(u,v)属于E，且顶点u为黑色，那么顶点v要么是灰色，要么是黑色。也就是说，与黑色顶点相邻的所有顶点都是已被发现的，灰色顶点可能会有一些白色的相邻顶点，它们代表了已被发现与未被发现顶点之间的边界。

伪代码

BFS(G, s)

for each vertex u (- V[G] - {s}
    do color[u] <- WHITE
         d[u] <- 00
         parent[u] <- NULL
color[s] <- GRAY
d[s] <- 0
parent[s] <- NULL
Q <- 空集
ENQUEUE(Q, s);
while Q != 空集
    do u <- DEQUEUE(Q)
        for each v (- Adj[u]
            do if color[v] == WHITE
                 then color[v] <- GRAY
                     d[v] <- d[u] + 1
                     parent[v] <- u
                     ENQUEUE(Q, v);
        color[u] <- BLACK

参考示例

(1) http://blog.csdn.net/zinss26914/article/details/8766119

(2) https://github.com/wangzhengyi/cracking_the_code_interview/blob/master/data_structures/4.2.c

深度优先搜索(DFS)

深度优先搜索所遵循的搜索策略是尽可能“深”地搜索一个图，对于新发现的顶点，如果它还有以此为起点而未探测到的边，就沿此边继续探测下去。当顶点v的所有边都已被探寻过后，搜索将回溯到发现顶点v有起始点的那些边，这一过程一直进行到已发现从源点可达的所有顶点为止。如果还存在未被发现的顶点，则选择其中一个作为源点，并重复以上过程。整个过程反复进行，知道所有的顶点都被已发现为止

伪代码

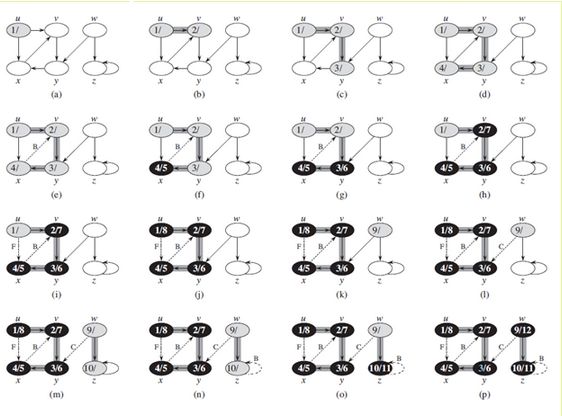
图示过程，当各条边被算法探索到时，他们或者被加以阴影（如果它们是树边），或者被标以虚线。对于非树边，根据他们是否反向，交叉或前向边等情况，将它们标记为B/C/F。对于各个顶点，根据它们的发现/完成时间，给它们加上时间戳。

参考示例

(1) http://blog.csdn.net/zinss26914/article/details/8941541

(2) http://blog.csdn.net/wzy_1988/article/details/9979877

最小生成树

假设要在n个城市之间建立通讯联络网，则连通n个城市只需要修建n-1条线路，如何在最省经费的前提下建立这个通讯网呢？答案就是最小生成树。

术语描述是：在e条带权的边中选取n-1条边（不构成回路），使权值之和最小。

如下图是一个无向连通图，图中显示各条边的权值，带阴影的边为最小生成树的边，树中各边的权值之和为37.最小生成树不是唯一的，用边(a,h)替代边(b,c)得到的是另外一颗最小生成树，各边权值之和也是37.

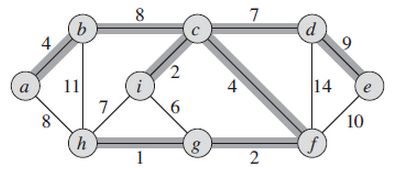
解决最小生成树问题有两种算法：kruskal算法和prim算法。在了解这两种算法之前，先得了解一下MST性质（最小生成树性质）：

设G = （V， E）是一个连通网络，U是顶点集V的一个真子集。若（u，v）是G中一条“一个端点在U中（例如u属于U），另一个端点不在U中的边（例如v属于V-U），且（u,v）具有最小权值，则一定存在G的一颗最小生成树包括此边(u,v).”通俗的讲，就是最小权值的边必定在最小生成树上，前提是，边的一个顶点在生成树上，另一个顶点不在（这里可以参考贪心算法的实现，而且kruskal和prim算法都是利用了贪心的思想）

kruskal算法

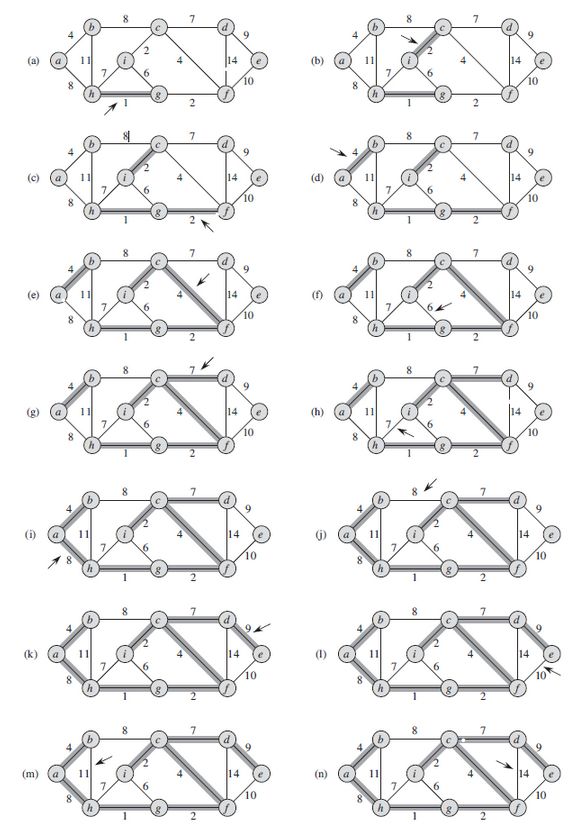
考虑问题的出发点：为使生成树上的边的权值之和达到最小，则应使生成树中每一条边的权值尽可能的小。具体做法：先构造一个只含n个顶点的子图SG（sub-graph），然后从权值最小的边开始，若它的添加不使SG中产生回路，则在SG上加上这条边，如此重复，直至加上n-1条边为止。图示如下：

简单的说，kruskal算法过程就是，每次寻找最小权值的边，然后加入到最小生成树中，这个过程用到的操作，就是并查集，find-set（u）返回最小包含u的集合中的一个代表元素（最小权值边的顶点），通过测试find-set（u）是否等价于find-set（v）判断顶点u和v是否属于同一棵树。通过union-set（u，v）实现树与树的合并。

伪代码如下：

MST-KRUSKAL(G, w)
A <- 空集
for each vertex v (- V[G]
    do MAKE-SET(v)
sort the edges of E into nondecreasing order by weight w
for each edge(u, v) (- E, taken in nondecreasing order by weight
    do if FIND-SET(u) != FIND-SET(v)
        then A <- A U {(u, v)}
            UNION-SET(u, v)
return A

参考示例

http://blog.csdn.net/zinss26914/article/details/8794018

prim算法

取图中任意一个顶点v作为生成树的根，之后往生成树上添加新的顶点u。在添加的顶点u和已经在生成树的顶点v之间必定存在一条边，并且改边的权值在所有连通顶点v和u之间的边中取值最小。之后继续往生成树上添加顶点，直至生成树上含有n-1个顶点为止。也就是，每次添加树中的边，都是树的权尽可能小的边。图示：

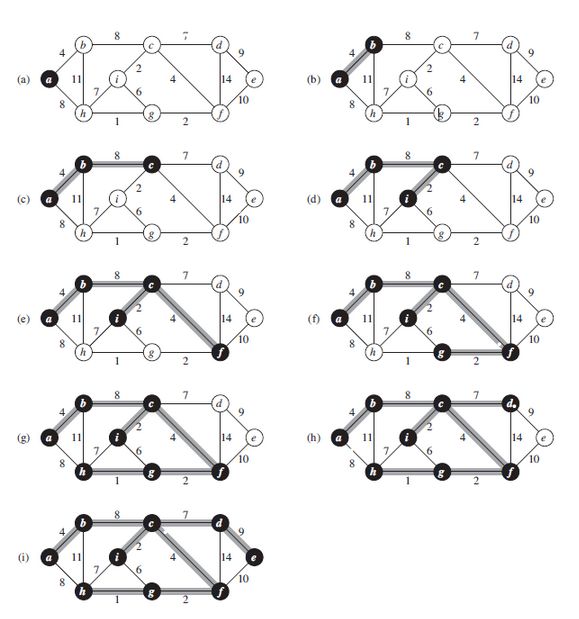
伪代码

MST-PRIME(G, w, r)
for each u (- V[G]
    do key[u] <- 无穷
        parent[u] <- null
key[r] <- 0
Q <- V[G]
while Q != 空集
    do u <- EXTRACT-MIN(Q)
        for each v (- Adj[u]
            do if v(- Q and w(u, v) < key[v]
                then parent[v] <- u
                   key[v] <- w(u, v)

参考链接

http://blog.csdn.net/zinss26914/article/details/8805035

kruskal和prime对比

过程简单对比

kruskal算法：所有的顶点放那，每次从所有的边中找一条代价最小的

prim算法：在U，（V-U）之间的边，每次找一条代价最小的

效率对比

效率上：

• 稠密图 prim > kruskal
• 稀疏图 kruskal > prim

拓扑排序

拓扑排序（Toplogical Sort），简单地说，由某个集合上的一个偏序得到该集合上的一个全序，这个操作称为拓扑排序

若集合X上的关系R是自反的、反对称的和传递的，则称R是集合X上的偏序关系

设R是集合X上的偏序，如果对每个x，y∈X，必有xRy或yRx，则称R是集合X上的全序关系

图示：

用顶点表示活动，用弧表示活动间的优先关系的有向图称为顶点表示活动的网（Activity On Vertex Network），简称AOV-网。在网中，若从顶点i到顶点j有一条有向路径，则i是j的直接前驱，j是i的直接后继

拓扑排序算法

1. 在有向图中选一个没有前驱的顶点输出
2. 从图中删除该顶点和所有以它为尾的弧
3. 重复1、2步骤，直至全部顶点均已输出，或者当图中不存在无前驱的顶点为止(说明有向图中有环)

伪代码实现

采用邻接矩阵作为存储图的数据结构，同时加上了一个入度数组indegree数组查找入度为0节点的辅助数组

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

// 图最大节点总数
#define MAX 502	

// 入度数组
int indegree[MAX];

// 图的邻接矩阵
int matrix[MAX][MAX];

/**
 * Description:邻接矩阵+入度数组实现拓扑排序
 */
void topological_sort(int n)
{
	int i, j, k;
	for (i = 0; i < n; i ++) {	// 每次循环确定全序序列的一个元素
		for (j = 1; j <= n; j ++) {
			if (indegree[j] == 0) {	// 选取一个没有前驱的节点输出
				indegree[j] --;
				if (i == n - 1) {
					printf("%d\n", j);
				}else {
					printf("%d ", j);
				}

				// 删除该节点和所有以它为尾的弧
				for (k = 1; k <= n; k ++) {
					if (matrix[j][k]) {
						matrix[j][k] = 0;
						indegree[k] -= 1;
					}
				}

				// 进行下一个循环
				break;
			}
		}
	}
}

参考题目

http://blog.csdn.net/zinss26914/article/details/8854232

参考链接

http://mindlee.net/2011/11/16/minimum-spanning-trees/