【排序算法】合并排序超级总结

一、介绍

基本的排序算法主要可以分为两大类。第一类时基于逐个比较的，第二类是非比较的。插入排序Insertion sort,冒泡排序bubble,和希尔排序Shell sort都是基于比较模型的。这三个算法的时间复杂度为O(n^2),实在是太慢了。是否有可能比O(n^2)更快的排序方法呢？答案当然是有的。

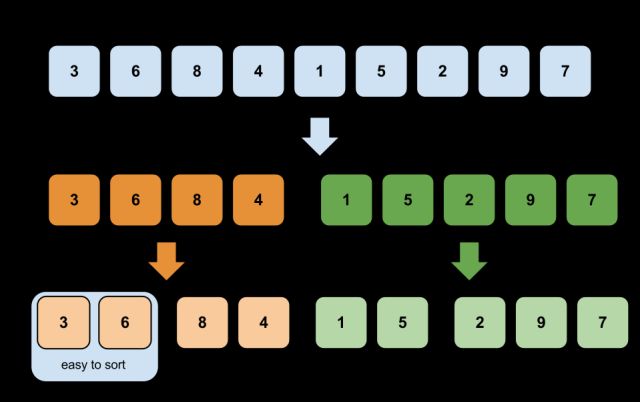
前面三种算法都是从待排序列表开始比较其中的每两个元素大小。插入排序和冒泡排序作了很多次比较，这正是合并排序所克服的。

所有我们需要将一个长的待排序列分割成比较小的序列，然后再进行排序，最后进行合并操作。所有合并排序可以分为“拆分和合并”两步来完成。

 

二、实现

合并排序速度比较快并且并不难实现，这对于开发人员来说至关重要，下面给出合并排序的C语言实现，合并排序可以分为递归形式和迭代形式实现，迭代形式比递归形式需要更多的存储空间，这里主要给出递归的实现方法：

(1)有序段合并函数

/*将有序断a[p]至a[q]段和有序段a[s]至a[t]段合并到b[p]至b[t],Len为数组长度*/
void merge(int a[],int p,int q,int s,int t,int Len) 
{   
	int n=10;
	int i,j,k;
	int *b=(int *)malloc(Len*sizeof(int));
	/*定义三个指针初值*/
   i=p;
   j=s;
   k=p-1;

while((i<=q)&&(j<=t)) //当两个有序段都不为空时
{
	if(a[i]<=a[j])
		b[++k]=a[i++]; //合并
	else
		b[++k]=a[j++];
}
while(i<=q) 	//处理有序段1剩下的元素
b[++k]=a[i++];
while(j<=t)             //处理有序段2剩下的元素
	b[++k]=a[j++];        

 for(i=p;i<=t;i++)      //将合并后的有序段移到源数组a
	 a[i]=b[i];
   

}

 

(2)主控函数

void merge_sort(int a[],int i,int j,int Len)
{
	int k;
	if(i<j)
	{
		k=(i+j)/2;    // K分段终点
		merge_sort(a,i,k,Len);  //对左端进行排序
		merge_sort(a,k+1,j,Len);
		merge(a,i,k,k+1,j,Len);   //合并左右端
	}
}

 调用方法：

void main()
{   
	
    int a[]={20,13,4,2,87,9,8,5,46,26};
	int Len=sizeof(a)/sizeof(int);
 	merge_sort(a,0,Len-1,Len);
 
	printf("排序后为：\n");
	for(int i=0;i<Len;i++)
		printf("%d ",a[i]);
}

三、复杂性

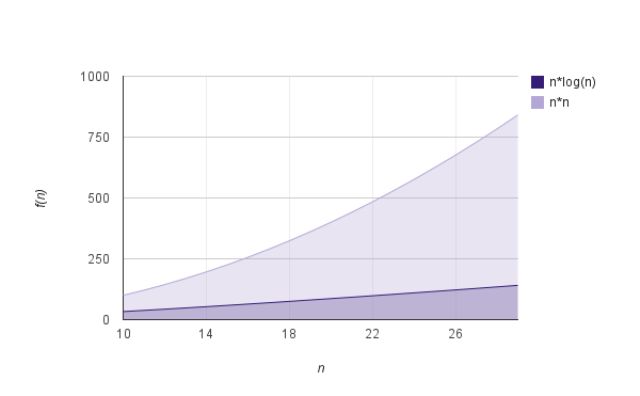
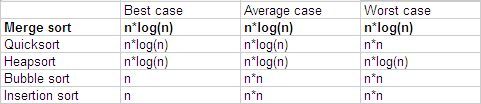
合并排序在最坏情况下的复杂度为O(n*log(n))，而快速排序在最坏情况下的复杂度为O(n²),并且合并排序是一个稳定的排序。

四、合并排序算法有效的两个原因

(1)不管输入是什么都非常快。

合并排序是一个稳定的并快速的排序算法，在最坏的情况下时间复杂度为O(n*log(n))，快速排序为O(n²)，当n=20时，快速排序比合并排序要慢4.6倍。由此可见，合并排序有很大的优势。

（2）容易实现。这对于开发者来说也是重要的原因。

五、合并排序算法失效的三个原因

(1)比基于非比较的排序算法慢。不过这取决于输入数据。

（2）。对于初学者来说比较难实现。尤其是对于合并部分。

（3）。当输入数据接近有序，合并排序的速度要比冒泡排序和插入排序要慢。因为插入排序和冒泡排序在最好的情况下的复杂度为O(n).而合并排序在最好的情况下时间复杂度为O(n*log(n))

综上所述，合并排序是一个实用很好的算法之一，因为他实现容易并且比较快，值得每一位开发者去学习。

复制 搜索

复制 搜索