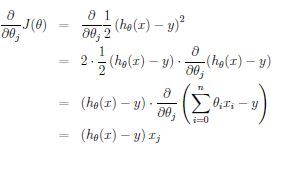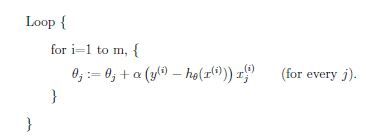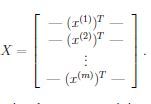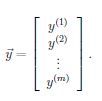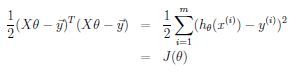Ng机器学习课程Notes学习及编程实战系列-Part 1 Linear Regression
编者按:本系列系统总结Ng机器学习课程(http://cs229.stanford.edu/materials.html) Notes理论要点,并且给出所有课程exercise的作业code和实验结果分析。”游泳是游会的“,希望通过这个系列可以深刻理解机器学习算法,并且自己动手写出work高效的机器学习算法code应用到真实数据集做实验,理论和实战兼备。
Part 1 Linear Regression
1. Supervised Learning
在Supervise Learning的Setting中,我们有若干训练数据(x^(i),y^(i)) i= 1,...,m ,这里i用于index training example。监督学习的任务就是要找到一个函数 (又称为模型或者假设hypothesis)H: X -> Y, 使得h(x)是相应值y的好的预测。整个过程可以描述为下图
当待预测的目标变量是连续型数据时,我们称之为回归(regression)问题;当待预测的目标变量是离散型数据时,我们称之为分类(classification)问题。因此回归问题和分类问题是监督学习针对连续型数据预测和离散型数据预测的两种典型学习问题。
2 Linear Regression
一般而言,我们会用feature向量来描述训练数据X,我们用x_j^i来表示,其中j用于index feature, i用于index训练样本。在监督学习里面,我们需要找到一个最佳的预测函数h(x),比如我们可以选取feature的线性组合函数
![]()
那么我们的问题就变成了要寻找最优的参数\theta可以使得预测的error最小。把这个函数用向量表示
机器学习里面一般默认变量为列向量,因此这里是参数向量\theta的转置矩阵。同时我们还加上了”feature 0“即x_0 = 1 以便方便表示成为向量乘积的形式。为了寻找最优的参数\theta,我们可以最小化error function即cost function
这个就是least-squares cost function,通过最小化这个函数来寻找最优参数。
3 LMS算法
为了寻找最优参数,我们可以随机初始化,然后沿着梯度慢慢改变参数值(需要改变\theta所有维),观察cost function值的变化,这就是梯度下降法的思想。假设我们只有一个训练样本(x,y), 对参数\theta_j求偏导数有
我们可以得到下面的参数update rule
![]()
其中\alpha叫learning rate,用于调节每次迭代参数变化的大小,这就是LMS(least mean squares)算法。用直观的角度去理解,如果我们看到一个训练样本满足y^(i) - h(x(i))等于0,那么说明参数就不必再更新;反之,如果预测值error较大,那么参数的变化也需要比较大。
如果我们有多个训练样本,比如有m个样本,每个样本用n个feature来描述,那么GD的update rule需要对n个feature对应的n个参数都做更新,有两种更新方式:batch gradient descent和stochastic/incremental gradient descent。对于前者,每次更新一轮参数\theta_j(注意n个参数需要同步更新才算完成一轮)需要都需要考虑所有的m个训练样本,即
也就是每更新一个\theta_j我们需要计算所有m个训练样本的prediction error然后求和。而后者更新一轮参数\theta_j我们只需要考虑一个训练样本,然后逐个考虑完所有样本(因此是incremental的)即
当训练样本size m非常大时,显然stochastic/incremental gradient descent会更有优势,因为每更新一轮参数不需要扫描所有的训练样本。
我们也可以把cost function写出矩阵相乘的形式,即令
则有
因此代价函数J可以写成
我们将J(\theta)对向量\theta求梯度(对于向量求导,得到的是梯度,是有方向的,这里需要用到matrix calculus,比标量形式下求导麻烦一些,详见NG课程notes),令梯度为0可以直接得到极值点,也就是唯一全局最优解情形下的最值点(normal equations)
![]()
这样可以避免迭代求解,直接得到最优的参数\theta值。
3 编程实战
(注:本部分编程习题全部来自Andrew Ng机器学习网上公开课)
3.1 单变量的Linear Regression
在单变量的Linear Regression中,每个训练样本只用一个feature来描述,例如某个卡车租赁公司分店的利润和当地人口总量的关系,给定若干人口总量和利润的训练样本,要求进行Linear Regression得到一条曲线,然后根据曲线对新的城市人口总量条件下进行利润的预测。
主程序如下
%% Initialization
clear ; close all; clc
%% ==================== Part 1: Basic Function ====================
% Complete warmUpExercise.m
fprintf('Running warmUpExercise ... \n');
fprintf('5x5 Identity Matrix: \n');
warmUpExercise()
fprintf('Program paused. Press enter to continue.\n');
pause;
%% ======================= Part 2: Plotting =======================
fprintf('Plotting Data ...\n')
data = load('ex1data1.txt');
X = data(:, 1); y = data(:, 2);
m = length(y); % number of training examples
% Plot Data
% Note: You have to complete the code in plotData.m
plotData(X, y);
fprintf('Program paused. Press enter to continue.\n');
pause;
%% =================== Part 3: Gradient descent ===================
fprintf('Running Gradient Descent ...\n')
X = [ones(m, 1), data(:,1)]; % Add a column of ones to x
theta = zeros(2, 1); % initialize fitting parameters
% Some gradient descent settings
iterations = 1500;
alpha = 0.01;
% compute and display initial cost
computeCost(X, y, theta)
% run gradient descent
theta = gradientDescent(X, y, theta, alpha, iterations);
% print theta to screen
fprintf('Theta found by gradient descent: ');
fprintf('%f %f \n', theta(1), theta(2));
% Plot the linear fit
hold on; % keep previous plot visible
plot(X(:,2), X*theta, '-')
legend('Training data', 'Linear regression')
hold off % don't overlay any more plots on this figure
% Predict values for population sizes of 35,000 and 70,000
predict1 = [1, 3.5] *theta;
fprintf('For population = 35,000, we predict a profit of %f\n',...
predict1*10000);
predict2 = [1, 7] * theta;
fprintf('For population = 70,000, we predict a profit of %f\n',...
predict2*10000);
fprintf('Program paused. Press enter to continue.\n');
pause;
%% ============= Part 4: Visualizing J(theta_0, theta_1) =============
fprintf('Visualizing J(theta_0, theta_1) ...\n')
% Grid over which we will calculate J
theta0_vals = linspace(-10, 10, 100);
theta1_vals = linspace(-1, 4, 100);
% initialize J_vals to a matrix of 0's
J_vals = zeros(length(theta0_vals), length(theta1_vals));
% Fill out J_vals
for i = 1:length(theta0_vals)
for j = 1:length(theta1_vals)
t = [theta0_vals(i); theta1_vals(j)];
J_vals(i,j) = computeCost(X, y, t);
end
end
% Because of the way meshgrids work in the surf command, we need to
% transpose J_vals before calling surf, or else the axes will be flipped
J_vals = J_vals';
% Surface plot
figure;
surf(theta0_vals, theta1_vals, J_vals)
xlabel('\theta_0'); ylabel('\theta_1');
% Contour plot
figure;
% Plot J_vals as 15 contours spaced logarithmically between 0.01 and 100
contour(theta0_vals, theta1_vals, J_vals, logspace(-2, 3, 20))
xlabel('\theta_0'); ylabel('\theta_1');
hold on;
plot(theta(1), theta(2), 'rx', 'MarkerSize', 10, 'LineWidth', 2);
首先load进训练数据,并且visualize出来
然后需要实现两个函数 computeCost 和graientDescent,分别计算代价函数和对参数按照梯度方向进行更新,结合Linear Regression代价函数计算公式和参数更新Rule,我们可以实现如下
function J = computeCost(X, y, theta) %COMPUTECOST Compute cost for linear regression % J = COMPUTECOST(X, y, theta) computes the cost of using theta as the % parameter for linear regression to fit the data points in X and y % Initialize some useful values m = length(y); % number of training examples % You need to return the following variables correctly J = 0; % ====================== YOUR CODE HERE ====================== % Instructions: Compute the cost of a particular choice of theta % You should set J to the cost. J = 1/(2 * m) * (X * theta - y)' * (X * theta - y); % ========================================================================= end
实现的时候要注意X是m行2列,theta是2行1列,y是m行1列。由于matlab默认矩阵是叉乘,要注意保证相乘的矩阵的维数满足叉乘的要求。参数更新函数如下
function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)
%GRADIENTDESCENT Performs gradient descent to learn theta
% theta = GRADIENTDESENT(X, y, theta, alpha, num_iters) updates theta by
% taking num_iters gradient steps with learning rate alpha
% Initialize some useful values
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);
for iter = 1:num_iters
% ====================== YOUR CODE HERE ======================
% Instructions: Perform a single gradient step on the parameter vector
% theta.
%
% Hint: While debugging, it can be useful to print out the values
% of the cost function (computeCost) and gradient here.
%
% Batch gradient descent
Update = 0;
for i = 1:m
Update = Update + alpha/m * (y(i) - X(i,:) * theta) * X(i, :)';
end
theta = theta + Update;
% ============================================================
% Save the cost J in every iteration
J_history(iter) = computeCost(X, y, theta);
end
end
这里用的是Batch Gradient Descent,也就是每更新一次参数都需要扫描所有m个训练样本。Update就是每次参数的变化量,需要对所有training example的训练误差进行求和。 每次更新参数后重新计算代价函数,把所有历史的cost记录保存在J_history中。经过1500次迭代,我们可以输出求的的参数theta,画出拟合的曲线,并且对新的人口来预测利润值,即
Running Gradient Descent ... ans = 32.0727 Theta found by gradient descent: -3.630291 1.166362 For population = 35,000, we predict a profit of 4519.767868 For population = 70,000, we predict a profit of 45342.450129 Program paused. Press enter to continue. Visualizing J(theta_0, theta_1) ...
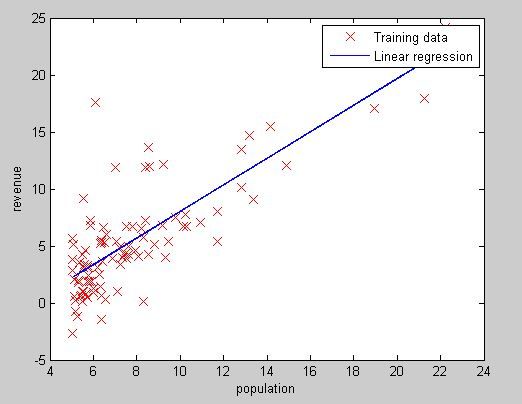
拟合出的曲线如下图
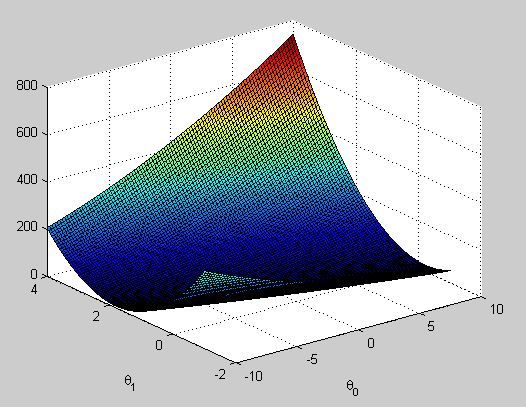
我们把cost function J的值在(theta_0, theta_1)上进行visualization可以得到
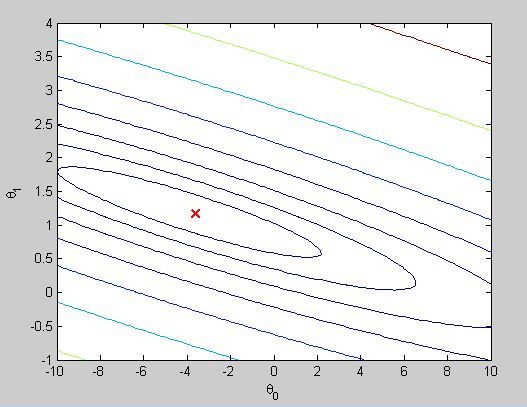
下面这张图是在(theta_0,theta_1)上的投影等高线图,红叉处就是GD收敛到的最小值处。对于linear regression只有全局最优解,所以这个也是我们想要的最优参数。
3.2 多变量的Linear Regression
如果每个训练样本用多个feature来描述,这就是多变量的Linear Regression问题。比如我们想根据房子的面积和卧室个数来预测房子的价格,那么现在每个训练样本就是用2个feature来描述。主程序如下
%% Initialization
%% ================ Part 1: Feature Normalization ================
%% Clear and Close Figures
clear ; close all; clc
fprintf('Loading data ...\n');
%% Load Data
data = load('ex1data2.txt');
X = data(:, 1:2);
y = data(:, 3);
m = length(y);
% Print out some data points
fprintf('First 10 examples from the dataset: \n');
fprintf(' x = [%.0f %.0f], y = %.0f \n', [X(1:10,:) y(1:10,:)]');
fprintf('Program paused. Press enter to continue.\n');
pause;
% Scale features and set them to zero mean
fprintf('Normalizing Features ...\n');
[X mu sigma] = featureNormalize(X);
% Add intercept term to X
X = [ones(m, 1) X];
%% ================ Part 2: Gradient Descent ================
% ====================== YOUR CODE HERE ======================
% Instructions: We have provided you with the following starter
% code that runs gradient descent with a particular
% learning rate (alpha).
%
% Your task is to first make sure that your functions -
% computeCost and gradientDescent already work with
% this starter code and support multiple variables.
%
% After that, try running gradient descent with
% different values of alpha and see which one gives
% you the best result.
%
% Finally, you should complete the code at the end
% to predict the price of a 1650 sq-ft, 3 br house.
%
% Hint: By using the 'hold on' command, you can plot multiple
% graphs on the same figure.
%
% Hint: At prediction, make sure you do the same feature normalization.
%
fprintf('Running gradient descent ...\n');
% Choose some alpha value
alpha = 0.01;
num_iters = 1000;
% Init Theta and Run Gradient Descent
theta = zeros(3, 1);
[theta, J_history] = gradientDescentMulti(X, y, theta, alpha, num_iters);
% Plot the convergence graph
figure;
plot(1:numel(J_history), J_history, '-b', 'LineWidth', 2);
xlabel('Number of iterations');
ylabel('Cost J');
% Display gradient descent's result
fprintf('Theta computed from gradient descent: \n');
fprintf(' %f \n', theta);
fprintf('\n');
% Estimate the price of a 1650 sq-ft, 3 br house
% ====================== YOUR CODE HERE ======================
% Recall that the first column of X is all-ones. Thus, it does
% not need to be normalized.
x_predict = [1 1650 3];
for i=2:3
x_predict(i) = (x_predict(i) - mu(i-1)) / sigma(i-1);
end
price = x_predict * theta;
% ============================================================
fprintf(['Predicted price of a 1650 sq-ft, 3 br house ' ...
'(using gradient descent):\n $%f\n'], price);
fprintf('Program paused. Press enter to continue.\n');
pause;
%% ================ Part 3: Normal Equations ================
fprintf('Solving with normal equations...\n');
% ====================== YOUR CODE HERE ======================
% Instructions: The following code computes the closed form
% solution for linear regression using the normal
% equations. You should complete the code in
% normalEqn.m
%
% After doing so, you should complete this code
% to predict the price of a 1650 sq-ft, 3 br house.
%
%% Load Data
data = csvread('ex1data2.txt');
X = data(:, 1:2);
y = data(:, 3);
m = length(y);
% Add intercept term to X
X = [ones(m, 1) X];
% Calculate the parameters from the normal equation
theta = normalEqn(X, y);
% Display normal equation's result
fprintf('Theta computed from the normal equations: \n');
fprintf(' %f \n', theta);
fprintf('\n');
% Estimate the price of a 1650 sq-ft, 3 br house
% ====================== YOUR CODE HERE ======================
x_predict = [1 1650 3];
price = x_predict * theta;
% ============================================================
fprintf(['Predicted price of a 1650 sq-ft, 3 br house ' ...
'(using normal equations):\n $%f\n'], price);
3.2.1 Feature Normalization
通过观察feature的特征可以知道,房子的面积的数值大约是卧室个数数值的1000倍左右,当遇到不同feature的数值范围差异非常显著的情况,需要先进行feature normalization,这样可以加快learning算法的收敛。要进行Feature Normalization,需要首先对每一列feature值计算均值\mu和标准差\sigma,然后normalization/scale 之后的feature值x'与原始feature值x满足 x' = (x - \mu) / \sigma 。即把原始的feature减去均值然后除以标准差。因此我们可以这样实现feature normalization的函数
3.2.2 Gradient Descent
这一步同样需要实现计算代价函数和更新参数的函数,对于多变量的线性回归,其代价函数也可以写成如下的向量化表示的形式
上面给出的单变量情形的代价函数和参数update rule同样适用于多变量情形,只是现在X有很多列,同样支持。注意这个时候没有办法在(\theta_0,\theta_1,\theta_2)上面可视化代价函数J,一共有四维。但是可以画出代价函数J随迭代次数的变化曲线如下
这里设置的learning rate \alpha = 0.01,迭代1000次,可以看出在400次左右时代价函数J就几乎收敛,不再变化。我们也可以调节learning rate \alpha, 选取合适的learning rate很重要,选得太小收敛很慢,选得太大有可能无法收敛(每次迭代参数变化太大,没法找到极值点)Ng建议选取\alpha时按照log scale,比如不断除以3,0.3 , 0.1 , 0.03 , 0.01 ...
3.2.3 Normal Equations
Alternately, 我们也可以直接用下面这个公式来计算最优的\theta,推导过程是代价函数对参数向量\theta求导数,令导数为0.
![]()
函数实现如下
function [theta] = normalEqn(X, y) %NORMALEQN Computes the closed-form solution to linear regression % NORMALEQN(X,y) computes the closed-form solution to linear % regression using the normal equations. theta = zeros(size(X, 2), 1); % ====================== YOUR CODE HERE ====================== % Instructions: Complete the code to compute the closed form solution % to linear regression and put the result in theta. % theta = inv(X'* X)*X'*y; % ============================================================ end
注意在GD中做预测时需要先对feature做normalization;在NE中做预测时不需要最feature做normalization。
综上所述,程序会先基于batch gradient descent 求最优\theta,然后对测试样本预测房价(注意feature normalization);然后基于normal equation直接算\theta,然后对测试样本预测房价。全部输出结果如下
Normalizing Features ... Running gradient descent ... Theta computed from gradient descent: 340397.963535 109848.008460 -5866.454085 Predicted price of a 1650 sq-ft, 3 br house (using gradient descent): $293237.161479 Program paused. Press enter to continue. Solving with normal equations... Theta computed from the normal equations: 89597.909543 139.210674 -8738.019112 Predicted price of a 1650 sq-ft, 3 br house (using normal equations): $293081.464335两次求的参数不同,因为前者有feature normalization,后者没有。对1650 sq-ft, 3 br house的房子预测的房价都在29万美元左右。