HDU 4872 ZCC Loves COT 对标记的标记打标记

原题：http://acm.hdu.edu.cn/showproblem.php?pid=4872

题意：给一个n*n*n的方体，定义两种操作，修改操作是给出x,y,z,a，把满足0 <= k <= j <= i < a的所有val[x+i][y+j][z+k]的值+1，询问操作类似询问这个区域的val和，更新和查询都是10W，n是100，所有更新都结束后才会开始查询

解题思路：

首先请看此题的一维版本：http://acm.hdu.edu.cn/showproblem.php?pid=1556

这道题目就很经典了，对于一次更新[l, r], 我们操作 a[l]++, a[r+1]-- ，然后求一次前缀和，就可以得到具体的 a[i] 的值

原理就是遇到+1表示有一次涂色从这里开始，遇到-1表示有一次涂色到此结束，具体就不在详细说了

对于这样的操作我们称为打标记

然后我们把他扩展到二维版本

定义修改操作是给出 x, y, a 对满足 0 <= j <= i < a 的所有 val[x+i][y+j] 的值 +1， 询问类似

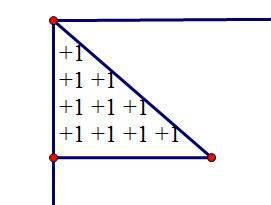
我们在平面首先画出这样一个区域

向下的是x + i的部分，向右是y + j部分，满足 j <= i 的部分画出来就是这样一个三角形

那么我们仿照一维的情况，对于每一行打标记，就变成了下面这样

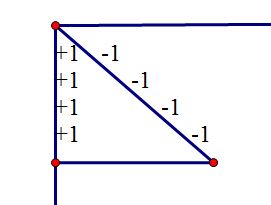
这时我们可以发现，标记是连续的一段，相当于我们对一维的线段打的两个点标记，在线段扩展到二维平面的同时，被拉伸成了线段

那么对于这个由标记生成的线段，我们仍然可以打标记，对于两个方向，分别打标记，一共四个，效果如下

竖直方向的+1， -1是每行 + 标记的标记，斜线方向的则是 - 的标记

注意 - 标记也是继续按 +1 -1来打标记，这时的前缀和表示有多少个 - 标记，而不是减了多少

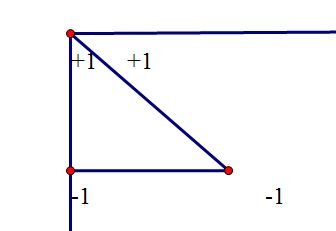
然后对于这两种标记，我们分别先沿向下和向右下的方向做一次前缀和，就可以还原出一维标记的情况

然后再从左向右累加，就可以得到具体元素的值

那么当我们得到具体元素的值之后，如何在O(1)效率求解任意三角形区域的sum值，还需要进一步讨论

根据一维前缀和，我们可以知道要想O(1)求解，必需通过类似前缀相减的方式，那么前缀本身不一定是线性的，只要他沿着若干方向一直扩展到边界，就可以是认为是前缀和

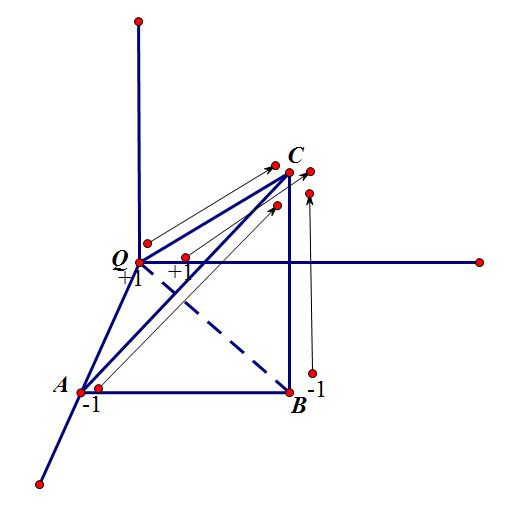
我们先讨论一个比较特殊的情况，就是询问的 x == y，如下图

Q点是我们询问的坐标(x, y), △QAD的区域就是我们要求sum值，通过一阵脑洞可以发现

△QAD = △AOB - △ QOC - 四边形CBDQ

而 四边形CBDQ = 四边形OBDE - 四边形OCQE

转化到这一步，所有的变量我们都可以通过一定姿势的前缀和求得了，我们用 tri[][] 来表示从点到x轴和原点构成的三角形区域，如 tri[A.x][A.y] = △AOB

再用 rec[][] 表示点到x轴y轴构成的区域，如 rec[D.x][D.y] = 四边形OBDE

则有 △QAD = tri[A] - tri[Q] - (rec[D] - rec[Q]) , tri和rec的预处理就很容易了，借助一下每行的前缀 pre[][]即可

另外一种情况就是 x != y, 这个时候和上面不一样的地方就是AQ延长线不过原点，那么图形不规则，似乎不符合我们上面的规律

但实际上由于外面区域都为0，所以可以假象扩大坐标系，把他弄到原点去，所以我们预处理前缀时只要按方向累加即可，不需要考虑太多

下面是将本题退化到二维情况的代码：

部分数组的含义如上文所示

其他的如 add[][] 表示一维 + 标记的再标记，sub为一维 - 标记的再标记

由于for循环的嵌套过于丧心病狂(主要是三维的时候)，于是我第一次define了for循环，REP什么的都比较常见了

<span style="font-family:Courier New;">//
#include <iostream>
#include <cstdio>
#include <cstring>
#include <ctime>
#include <cstdlib>
using namespace std;

#define LL long long
#define REP(i,a,b) for(int i = a; i <= b; ++i)

typedef LL Node[105][105];

Node val, add, sub, pre, tri, rec;

void init() {
    memset(add, 0, sizeof(add));
    memset(sub, 0, sizeof(sub));
}

void upd(int x, int y, int a) {
    ++add[x][y];
    --add[x + a][y];
    ++sub[x][y + 1];
    --sub[x + a][y + a + 1];
}

void solve(int n) {
    REP(i,1,n) REP(j,1,n) {
        add[i][j] += add[i - 1][j];
        sub[i][j] += sub[i - 1][j - 1];
        val[i][j] = val[i][j - 1] + add[i][j] - sub[i][j];
        pre[i][j] = pre[i][j - 1] + val[i][j];
        rec[i][j] = rec[i - 1][j] + pre[i][j];
        tri[i][j] = tri[i - 1][j - 1] + pre[i][j];
    }
}

LL cal(int x, int y, int a) {
    --x, --y;
    LL ans = 0;
    ans += tri[x + a][y + a] - tri[x][y];
    ans -= rec[x + a][y] - rec[x][y];
    return ans;
}

int main()
{
    int n, m, q, x, y, a;
    while( scanf( "%d%d%d", &n, &m, &q ) != EOF ) {
        init();
        while( m-- ) {
            scanf( "%d%d%d", &x, &y, &a );
            upd(x, y, a);
        }
        solve(n);
        while( q-- ) {
            scanf( "%d%d%d", &x, &y, &a );
            printf( "%lld\n", cal(x, y, a) );
        }
    }
    return 0;
}</span>

那么下面我们继续讨论扩展到三维的情况：

友情提示请先弄清楚二维的情况，并自备墨镜，下面的图形将开始各种丧心病狂

首先我们根据一维到二维的情况，一维的标记扩展后被拉伸成了线段，那么二维的标记在扩展到三维的情况时，是不是也一样是拉伸成线段？

这个不难想通，把上面那个二维标记的平面，沿z轴向上拉伸，三角形变成四面体，四个标记变成了四个线段

实质上把拉伸后的每一层(垂直 z 轴切下来一片)，他和上面二维的情况是完全一致的，只是三角形的大小在变化，图形如下

这个图形是在更新点Q展开的坐标系，不是从原点，四面体的性质可以这样考虑

原来是一个方体，为了保证i >= j，垂直XOY平面沿x == y切一刀，同理垂直YOZ平面对y == z切一刀，就行了

首先我们考虑QAB那个三角形，其实就是二维那个三角形，然后把这个三角形像C拉伸，那些标记也沿着拉伸方向变成线段

所以我们可以在那四个标记的位置再打标记 +1，在C点附近四个线段结束的地方再打标记 -1

具体的二维标记拉伸出来的效果我就不画了，沿着箭头方向一路写过去就行，你们脑补一下....

然后我们从这四个方向前缀和一下(当然我们又得开4个数组来记录这四条线段的信息), 就可以还原二维的标记add 和 sub数组，然后z那一位就搞定了，问题退化成二维状态

我之后的代码分别用A, B, C, D 四个数组来处理，如果你想通了二维的情况，这里就不难理解了，否则基本GG思密达

接下来我们再讨论怎么O(1)求这个四面体的Sum(val)

根据我们二维是得到的结论，我们用特殊图形(x == y)讨论出的规律，对任意情况适用，所以我们这里仍然使用(x == y == z)的特殊点来讨论

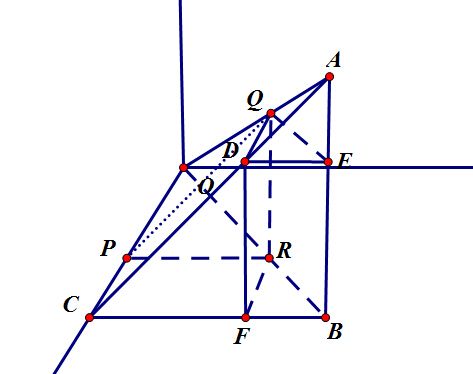
下面这个图比较残暴

我们要求的就是 四面体QADE

首先我们看到那个显眼的点A，可以想(nao)到(bu)应该用 四面体OABC - 四面体OPQR

所以我们用 tet[A] 来保存类似四面体OABC的前缀

然后我们还需要减去 三棱柱DCF-QPR 和 三棱柱QDE-RFB

对于三棱柱DCF-QPR 我们显然可以通过保存到YOZ平面的三棱柱的总和 psm[][][]，用psm[D] - psm[Q]来获得这一部分的值

那么还剩下 三棱柱QDE-RFB，你看到RFB那个三角形，就差不多能联想到二维那个图形了，是一样的

RFB = OBC - ORP - (PCFR) ，这里PCFR怎么来也很显然，把这四个前缀都加一维就可以了

于是我们需要四类前缀来获得QADE的值，当然预处理这四类前缀还需要其他的辅助数组

最终代码：

部分上文提到的变量就不说了

pre[i][j][k] 保存 val[i][j][1 ~ k], sum[][][]保存类似QPR那样的三角形片，用来再沿x方向累加得到psm， tet什么的

tot[][][] 用了保存需要用到的那个长方体

(PS：这一部分还是弄懂了自己推好点，用到的变量名太多了，英语渣的表示压力很大)

<span style="font-family:Courier New;">//
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;

#define LL long long
#define REP(i,a,b) for(int i = a; i <= b; ++i)

typedef LL Node[105][105][105];

Node val, add, sub, A, B, C, D;
Node pre, sum, tot, tri, rec, psm, tet;

void init() {
    memset(A, 0, sizeof(A));
    memset(B, 0, sizeof(B));
    memset(C, 0, sizeof(C));
    memset(D, 0, sizeof(D));
}

void upd(int x, int y, int z, int a) {
    ++A[x][y][z];
    --A[x + a][y + a][z + a];
    ++B[x + a][y][z];
    --B[x + a][y + a][z + a];
    ++C[x][y + 1][z];
    --C[x + a][y + a + 1][z + a];
    ++D[x + a][y + a + 1][z];
    --D[x + a][y + a + 1][z + a];
}

void solve(int n) {
    REP(i,1,n) REP(j,1,n) REP(k,1,n) {
        A[i][j][k] += A[i - 1][j - 1][k - 1];
        B[i][j][k] += B[i][j - 1][k - 1];
        C[i][j][k] += C[i - 1][j - 1][k - 1];
        D[i][j][k] += D[i][j][k - 1];
    }
    REP(i,1,n) REP(j,1,n) REP(k,1,n) {
        add[i][j][k] = A[i][j][k] - B[i][j][k];
        add[i][j][k] += add[i - 1][j][k];
        sub[i][j][k] = C[i][j][k] - D[i][j][k];
        sub[i][j][k] += sub[i - 1][j - 1][k];
        val[i][j][k] = val[i][j - 1][k] + add[i][j][k] - sub[i][j][k];
    }
    REP(i,1,n) REP(j,1,n) REP(k,1,n) {
        pre[i][j][k] = pre[i][j][k - 1] + val[i][j][k];
        sum[i][j][k] = sum[i][j - 1][k - 1] + pre[i][j][k];
        tot[i][j][k] = tot[i][j - 1][k] + pre[i][j][k];
        tri[i][j][k] = tri[i - 1][j - 1][k] + tot[i][j][k];
        rec[i][j][k] = rec[i - 1][j][k] + tot[i][j][k];
        psm[i][j][k] = psm[i - 1][j][k] + sum[i][j][k];
        tet[i][j][k] = tet[i - 1][j - 1][k - 1] + sum[i][j][k];
    }
}

LL cal(int x, int y, int z, int a) {
    --x, --y, --z;
    LL ans = 0, tmp = 0;
    ans += tet[x + a][y + a][z + a] - tet[x][y][z];
    ans -= psm[x + a][y][z] - psm[x][y][z];
    tmp += tri[x + a][y + a][z] - tri[x][y][z];
    tmp -= rec[x + a][y][z] - rec[x][y][z];
    ans -= tmp;
    return ans;
}

int main()
{
    int n, m, q, x, y, z, a;
    while( scanf( "%d%d%d", &n, &m, &q ) != EOF ) {
        init();
        while( m-- ) {
            scanf( "%d%d%d%d", &x, &y, &z, &a );
            upd(x, y, z, a);
        }
        solve(n);
        while( q-- ) {
            scanf( "%d%d%d%d", &x, &y, &z, &a );
            printf( "%lld\n", cal(x, y, z, a));
        }
    }
    return 0;
}</span>