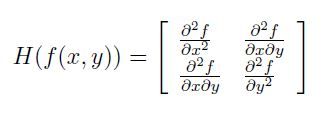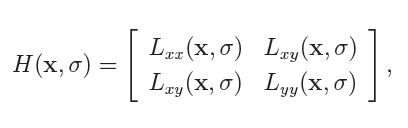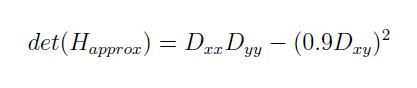图像特征提取4：Surf特征

一、Surf描述子形成步骤

         1. 构造高斯金字塔尺度空间

         其实surf构造的金字塔图像与sift有很大不同，就是因为这些不同才加快了其检测的速度。Sift采用的是DOG图像，而surf采用的是Hessian矩阵行列式近似值图像。首先来看看图像中某个像素点的Hessian矩阵，如下：

　　        

         即每一个像素点都可以求出一个Hessian矩阵。但是由于我们的特征点需要具备尺度无关性，所以在进行Hessian矩阵构造前，需要对其进行高斯滤波。这样，经过滤波后在进行Hessian的计算，其公式如下：

　　 

 

     为了减小计算量，作者利用了积分图像来计算上式（大大的减少计算量），方法其实很简单就是在高斯模糊的基础上将原来的模块近似下。

对于一般计算图像的二阶导时，我们利用公式d²f(x)/dx²=(f(x+1)-f(x))-(f(x)-f(x-1))=-2*f(x)+f(x+1)+f(x-1)。但是f(x)=g(h(x))【h(x)为图像的灰度值，f(x)是将h(x)高斯滤波处理的灰度函数 】

     以9X9滤波器为例，如上图所示，左边两幅图分别为灰度图像在中心点（黑色点）处的二阶导数d²f(x)/dx²和d²f(x)/dxdy的模板对应的值, 近似后变成右边的两幅图，图中灰色部分像素值为0。但是这样计算特征值也很复杂，所以作者提供了一种新思路--使用积分图像。

绿色的部分为当前像素点，红色为积分区域。这样计算图像中任意一块矩形区域的灰度之和Sx只需要利用矩形4个顶点(Xi,Yi)(i=1,2,3,4  顺序为从上之下，先左后右)的积分值S（x,y）即可。

                                   Sx=S(X1,Y1)+ S(X4,Y4)-S(X2,Y2)-S(X3,Y3)

读者从以上应该可以看出积分图像的好处了，我们只要在函数定义之前计算积分图像，然后就能快速求出hessian的特征值。

         最终我们要的是原图像的一个变换图像，因为我们要在这个变换图像上寻找特征点，然后将其位置反映射到原图中，例如在sift中，我们是在原图的DOG图上寻找特征点的。那么在surf中，这个变换图是什么呢？就是原图每个像素的Hessian矩阵行列式的近似值构成的。其行列式近似公式如下：

　　        

         这里Dxx和Dxy就是根据Figure2得到的,其中0.9是作者给出的一个经验值，其实它是有一套理论计算的，具体去看surf的英文论文。

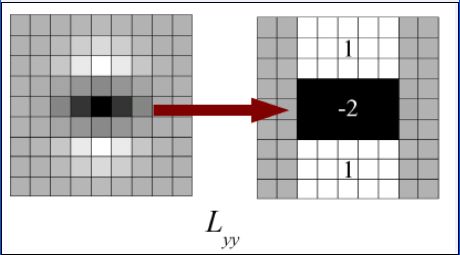
         由于求Hessian时要先高斯平滑，然后求二阶导数，这在离散的像素点是用模板卷积形成的，这2中操作合在一起用一个模板代替就可以了，比如说y方向上的模板如下：

　　　　        

         该图的左边即用高斯平滑然后在y方向上求二阶导数的模板，为了加快运算用了近似处理，其处理结果如右图所示，这样就简化了很多。并且右图可以采用积分图来运算，大大的加快了速度，关于积分图的介绍，可以去查阅相关的资料。

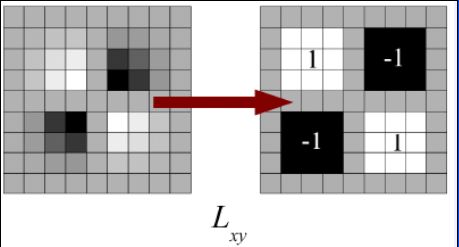
         同理，x和y方向的二阶混合偏导模板如下所示：

　　　　

 

　　上面讲的这么多只是得到了一张近似hessian行列式图，这例比sift中的DOG图，但是在金字塔图像中分为很多层，每一层叫做一个octave，每一个octave中又有几张尺度不同的图片。在sift算法中，同一个octave层中的图片尺寸(即大小)相同，但是尺度(即模糊程度)不同，而不同的octave层中的图片尺寸大小也不相同，因为它是由上一层图片降采样得到的。在进行高斯模糊时，sift的高斯模板大小是始终不变的，只是在不同的octave之间改变图片的大小。而在surf中，图片的大小是一直不变的，不同的octave层得到的待检测图片是改变高斯模糊尺寸大小得到的，当然了，同一个octave中的图片用到的高斯模板尺度也不同。Surf采用这种方法节省了降采样过程，其处理速度自然也就提上去了。其金字塔图像如下所示：

　　

　　　　

 

　　2. 利用非极大值抑制初步确定特征点

　　此步骤和sift类似，将经过hessian矩阵处理过的每个像素点与其3维领域的26个点进行大小比较，如果它是这26个点中的最大值或者最小值，则保留下来，当做初步的特征点。

 

　　3. 精确定位极值点

　　这里也和sift算法中的类似，采用3维线性插值法得到亚像素级的特征点，同时也去掉那些值小于一定阈值的点。

 

　　4. 选取特征点的主方向。

　　这一步与sift也大有不同。Sift选取特征点主方向是采用在特征点领域内统计其梯度直方图，取直方图bin值最大的以及超过最大bin值80%的那些方向做为特征点的主方向。而在surf中，不统计其梯度直方图，而是统计特征点领域内的harr小波特征。即在特征点的领域(比如说，半径为6s的圆内，s为该点所在的尺度)内，统计60度扇形内所有点的水平haar小波特征和垂直haar小波特征总和，haar小波的尺寸变长为4s，这样一个扇形得到了一个值。然后60度扇形以一定间隔进行旋转，最后将最大值那个扇形的方向作为该特征点的主方向。该过程的示意图如下：

　　　　

 

　　5. 构造surf特征点描述算子

　　在sift中，是在特征点周围取16*16的邻域，并把该领域化为4*4个的小区域，每个小区域统计8个方向梯度，最后得到4*4*8=128维的向量，该向量作为该点的sift描述子。

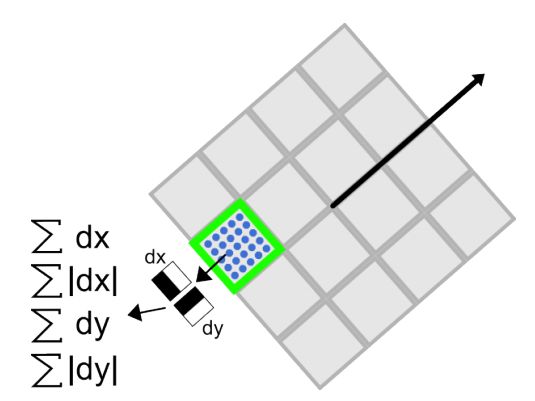
　　在surf中，也是在特征点周围取一个正方形框，框的边长为20s(s是所检测到该特征点所在的尺度)。该框带方向，方向当然就是第4步检测出来的主方向了。然后把该框分为16个子区域，每个子区域统计25个像素的水平方向和垂直方向的haar小波特征，这里的水平和垂直方向都是相对主方向而言的。该haar小波特征为水平方向值之和，水平方向绝对值之和，垂直方向之和，垂直方向绝对值之和。该过程的示意图如下所示：

　　　　

 

　　这样每个小区域就有4个值，所以每个特征点就是16*4=64维的向量，相比sift而言，少了一半，这在特征匹配过程中会大大加快匹配速度。

 

 

　　二、特征点的匹配过程

　　surf特征点的匹配过程和sift类似，这里不做详细介绍