Dimensionality Reduction（学习Free Mind知识整理）



阅读http://blog.pluskid.org/?p=290文章中的一些知识整理：学习的知识点降维。

=====================================================================

先看一下这句话“feature selection 和 dimensionality reduction 两个 topic 都有许多很经典的算法。前者通常是选出重要的 feature 的维度（并抛弃不重要的维度），而后者则是更广泛意义上的把一个高维的向量映射为一个低维向量，亦即“降维”，得到的结果 feature 的值已经不一定是原始的值，也可以把 feature selection 看作是 dimensionality reduction 的一种特殊情况。”（阉割和压缩的区别 -----网友解释）

我认为特征选择======>取其精华，去其糟粕;数据降维 ===>合理的信息丢失的范围里面 将原来的高维数据 映射到 一个低维空间里面 这样可以降低模型的复杂度和计算的复杂度 减少过拟合和增加泛化的能力,数据降维后不一定就直接按照降维后的维度作为特征的维度。

因为经常会遇到论文里面的泛化能力的评估，一直不是很清楚泛化能力怎么增强？什么鬼。。。。

所谓泛化能力（generalization ability）是指对新鲜样本的适应能力，对于测试网络模型的泛化能力啊算法的泛化能力啊，这个算法或者模型能有对新来的数据有好的准确率或者学习率，可能解释不是很到位，大概就是这个意思吧。

然后就是一个网络的泛化能力增强？

1、较多的输入样本但不是太多，过多的样本导致过度拟合，泛化能力不佳；样本包括至少一次的转折点数据。

2、隐含层神经元数量的选择，不影响性能的前提下，尽量选择小一点的神经元数量。隐含层节点太多，造成泛化能力下降，造火箭也只要几十个到几百个神经元，拟合几百几千个数据何必要那么多神经元？

3、误差小，则泛化能力好；误差太小，则会过度拟合，泛化能力反而不佳。

4、学习率的选择，特别是权值学习率，对网络性能有很大影响，太小则收敛速度很慢，且容易陷入局部极小化；太大则，收敛速度快，但易出现摆动，误差难以缩小；一般权值学习率比要求误差稍微稍大一点点；另外可以使用变动的学习率，在误差大的时候增大学习率，等误差小了再减小学习率，这样可以收敛更快，学习效果更好，不易陷入局部极小化。

5、训练时可以采用随时终止法，即是误差达到要求即终止训练，以免过度拟合；可以调整局部权值，使局部未收敛的加快收敛。

====================================================================

PCA的中投影不懂，看了 http://blog.codinglabs.org/articles/pca-tutorial.html  明白了，

原理（ http://blog.csdn.net/langb2014/article/details/48463139 ）也很清晰不错。我把点积和矩阵乘法混了，导致没理解。。。。

一、主元成份分析（PCA）对输入数据的要求?

1.线形性假设。

PCA的内部模型是线性的。这也就决定了它能进行的主元分析之间的关系也是线性的。现在比较流行的kernel-PCA的一类方法就是使用非线性的权值对原有PCA技术的拓展。
2.使用中值和方差进行充分统计。

使用中值和方差进行充分的概率分布描述的模型只限于指数型概率分布模型。（例如高斯分布），也就是说，如果我们考察的数据的概率分布并不满足高斯分布或是指数型的概率分布，那么PCA将会失效。在这种模型下，不能使用方差和协方差来很好的描述噪音和冗余，对教化之后的协方差矩阵并不能得到很合适的结果。事实上，去除冗余的最基础的方程是：其中 代表概率分布的密度函数。基于这个方程进行冗余去除的方法被称作独立主元分析(ICA)方法(Independent Component Analysis)。不过，所幸的是，根据中央极限定理，现实生活中所遇到的大部分采样数据的概率分布都是遵从高斯分布的。所以PCA仍然是一个使用于绝大部分领域的稳定且有效的算法。
3.大方差向量具有较大重要性。

PCA方法隐含了这样的假设：数据本身具有较高的信噪比，所以具有最高方差的一维向量就可以被看作是主元，而方差较小的变化则被认为是噪音。这是由于低通滤波器的选择决定的。
4.主元正交。PCA方法假设主元向量之间都是正交的，从而可以利用线形代数的一系列有效的数学工具进行求解，大大提高了效率和应用的范围。

二、输入需要满足高斯么？

这个问题请教了大牛，因为有时数据的分布并不是满足高斯分布。在非高斯分布的情况下，PCA方法得出的主元可能并不是最优的。在寻找主元时不能将方差作为衡量重要性的标准。要根据数据的分布情况选择合适的描述完全分布的变量，然后根据概率分布式来计算两个向量上数据分布的相关性。等价的，保持主元间的正交假设，寻找的主元同样要使。这一类方法被称为独立主元分解(ICA)。

三、样本数和特征维数有要求么？

pca降维不需要样本的个数大于特征的维数，没有特别要求，如果降维到30*29，这个是因为映射到另一个空间了，无需担心丢失了很多信息，并非特征选择直接丢掉了特征了，只是在另一个空间而已表达出原空间的高维。因此，要保证训练样本和测试样本被映射到同一个特征空间，这样才能保证数据的一致性。

四、对于维数比较大的数据，容易内存溢出？

princomp这个matlab自带的函数，在降维之前就将每一个样本减去了一个所有样本的平均值，也可能有很多样本没有减去平均值。princomp这里使用一行表示一个样本，每行包括这个样本的所有的特征值。而网上大部分都是每一列表示一个样本，这样这一列的所有行都表示这个样本的特征值。网上的程序使用列表示样本是有一定好处的，比如样本是1000000*30，总共有30个训练样本，每个样本的特征值个数是1000000，那么这个矩阵获得的协方差矩阵是30*30，计算起来非常的方便，不想30*1000000这样的矩阵获得到的协方差矩阵式1000000*1000000，直接就内存溢出了，不过matlab有自己的实现方式，巧妙的解决了这个问题。

=====================================================================

关于LSA的详细介绍和解释到 http://blog.csdn.net/langb2014/article/details/48464445 文章看看。

=====================================================================

关于Laplacian Eigenmap拉普拉斯特征映射：（ http://www.cnblogs.com/xbinworld/archive/2012/11/29/2795287.html ）

它的直观思想是希望相互间有关系的点（在图中相连的点）在降维后的空间中尽可能的靠近。Laplacian Eigenmaps可以反映出数据内在的流形结构。

Laplacian Eigenmaps也通过构建相似关系图（对应的矩阵为）来重构数据流形的局部结构特征。Laplacian Eigenmaps算法的主要思想是，如果两个数据实例i和j很相似，那么i和j在降维后目标子空间中应该尽量接近。设数据实例的数目为n，目标子空间的维度为m。定义大小的矩阵，其中每一个行向量是数据实例i在目标m维子空间中的向量表示，Laplacian Eigenmaps要优化的目标函数如下

(2.11)

定义对角矩阵，对角线上位置元素等于矩阵的第i行之和，经过线性代数变换，上述优化问题可以用矩阵向量形式表示如下：

(2.12)

其中矩阵是图拉普拉斯矩阵。限制条件保证优化问题有解，并且保证映射后的数据点不会被“压缩”到一个小于m维的子空间中。使得公式最小化的Y的列向量是以下广义特征值问题的m个最小非0特征值（包括重根）对应的特征向量：

(2.13)

 

 

使用时算法具体步骤为：

步骤1：构建图

使用某一种方法来将所有的点构建成一个图，例如使用KNN算法，将每个点最近的K个点连上边。K是一个预先设定的值。

步骤2：确定权重

确定点与点之间的权重大小，例如选用热核函数来确定，如果点i和点j相连，那么它们关系的权重设定为：

(2.14)

另外一种可选的简化设定是如果点i，j相连，否则。

步骤3：特征映射

计算拉普拉斯矩阵L的特征向量与特征值：

其中D是对角矩阵，满足，。

使用最小的m个非零特征值对应的特征向量作为降维后的结果输出。

前面提到过，Laplacian Eigenmap具有区分数据点的特性，可以从下面的例子看出：

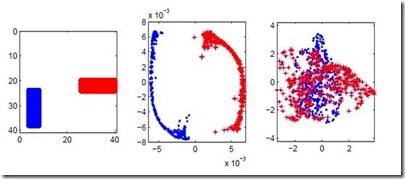
图1 Laplacian Eigenmap实验结果

见图1所示，左边的图表示有两类数据点（数据是图片），中间图表示采用Laplacian Eigenmap降维后每个数据点在二维空间中的位置，右边的图表示采用PCA并取前两个主要方向投影后的结果，可以清楚地看到，在此分类问题上，Laplacian Eigenmap的结果明显优于PCA。

 

图2 roll数据的降维

图2说明的是，高维数据（图中3D）也有可能是具有低维的内在属性的（图中roll实际上是2D的），但是这个低维不是原来坐标表示，例如如果要保持局部关系，蓝色和下面黄色是完全不相关的，但是如果只用任何2D或者3D的距离来描述都是不准确的。

代码实现：

% Laplacian Eigenmap ALGORITHM (using K nearest neighbors)
%
% [Y] = le(X,K,dmax)
%
% X = data as D x N matrix (D = dimensionality, N = #points)
% K = number of neighbors
% dmax = max embedding dimensionality
% Y = embedding as dmax x N matrix
 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
function [Y] = leigs(X,K,d)
 
[D,N] = size(X);
fprintf(1,'LE running on %d points in %d dimensions\n',N,D);
 
 
% STEP1: COMPUTE PAIRWISE DISTANCES & FIND NEIGHBORS 
fprintf(1,'-->Finding %d nearest neighbours.\n',K);
 
X2 = sum(X.^2,1);
distance = repmat(X2,N,1)+repmat(X2',1,N)-2*X'*X;
 
[sorted,index] = sort(distance);
neighborhood = index(2:(1+K),:);
 
 
 
% STEP2: Construct similarity matrix W
fprintf(1,'-->Constructing similarity matrix.\n');
 
W = zeros(N, N);
for ii=1:N
    W(ii, neighborhood(:, ii)) = 1;
    W(neighborhood(:, ii), ii) = 1;
end
 
% STEP 3: COMPUTE EMBEDDING FROM EIGENVECTS OF L
fprintf(1,'-->Computing embedding.\n');
 
D = diag(sum(W));
L = D-W;
 
% CALCULATION OF EMBEDDING
options.disp = 0; options.isreal = 1; options.issym = 1; 
[Y,eigenvals] = eigs(L,d+1,0,options);
Y = Y(:,2:d+1)'*sqrt(N); % bottom evect is [1,1,1,1...] with eval 0
 
 
fprintf(1,'Done.\n');
 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

=====================================================================

关于Locally Linear Embedding介绍， http://www.cnblogs.com/xbinworld/archive/2012/07/09/LLE.html

=====================================================================

作者kid介绍的降维方法站的高度比较高，有些观点理解不了，慢慢不断的认识进步理解吧，有独到见解的可以留言给我，非常感谢。 

=====================================================================

一个不错的链接：

http://www.cnblogs.com/gaoshangbing/archive/2010/03/23/1692357.html