深入理解Aho-Corasick自动机算法

前言：

  我总是对那些具有状态转移过程的算法，心怀敬意。

  例如：递归、递推、动规、DAT以及现在要说的AC自动机算法。

  数学真是优美！

                                         —— 致那些牛逼到不行的数学家们

本文链接：http://blog.csdn.net/lemon_tree12138/article/details/49335051 --编程小笙
                                                                 --转载请注明出处

概述：

  Aho-Corasick automaton(后面心均以AC代替)，该算法在1975年产生于贝尔实验室，是著名的多模匹配算法之一。

  AC自动机算法分为3步：构造一棵Trie树，构造失效指针和模式匹配过程。而这3步就是AC自动机算法的精髓所在，分别对应我们后面马上要说的3个函数：success,failure和emits.

特别说明：

0.学前导读：

  在学习本文之前，需要两个方面的知识背景。一个是Trie树，一个是KMP算法。大家可以移步到两面的两个链接中，学习一下。之后，回过头来再看我们的AC自动机，就可以会比较容易消化，也能更容易理解其中的精髓。

  《数据结构：字典树的基本使用》

  《算法：模式匹配之KMP算法》

1.本文参考：

  《Aho-Corasick算法的Java实现与分析-码农场》

一睹为快：

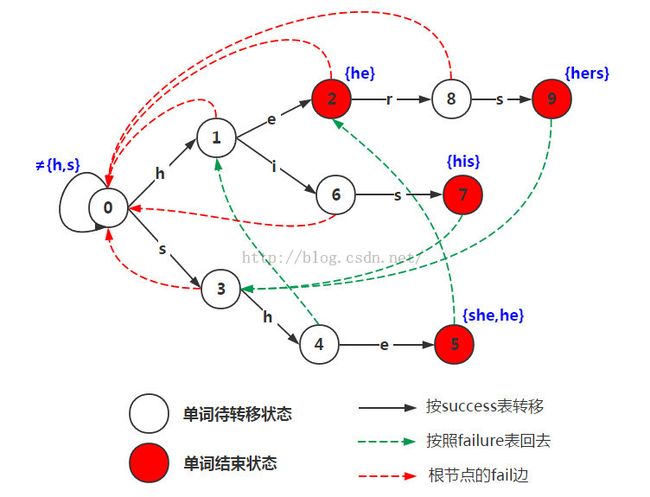
  以经典的ushers为例，模式串是he/ she/ his /hers，文本为“ushers”。构建的自动机如图：

原理说明：

0.算法比较

  正如前面所说，AC算法是基于Trie树且是KMP模式匹配算法的扩展。那么这里我们就可以从两个方面来作为切入点，详细说明一下AC算法或是AC自动机究竟是何物。

  首先明白两点：Trie树的核心点是状态转移，KMP模式匹配的核心点是减少重复匹配。

  先说Trie树吧。在之前的博客中，我还是用了很多的篇幅来说Trie树，不算这一篇的话，也有3篇文章或多或少都和Trie树扯上点边儿。前面的Trie树中，每个节点既是字符本身，又是节点的状态(DAT则不是这样)。节点为字符本身，这个好理解，那又是节点的状态这个要怎么解释呢？因为我们知道，当我们在遍历的过程中，走到某一个点的时候，比如说：目前有两个字典字符串：T1："abcde"和T2："abdef"，当我们在遍历的过程中走了"abcd"且停在了'd'字符上.这个时候，我们可以认定目前是处于字符串T1上的。因为当前节点可以代表其状态。而在T1和T2中，两个'd'节点的状态是不同的。而Trie树的状态转移则可以理解为，我们在遍历到节点d的时候，动态确定节点d的下一个状态，即节点e。

  再说说KMP模式匹配。在KMP模式匹配的过程中，我们使用到了一个next函数(如果你高兴，也可以说这是一张next表)。next函数的作用是，当我们在匹配的过程中，发生了匹配失败的时候，可以将模式串向前滑动n个字符，从而省去了n次的比较操作。而具体的操作方法及说明，我在之前的博客中也有介绍，这里不再详细说明。

  试想一下，如果我们要匹配一个文本文件d(举例文件的目的是为了说明，这个匹配字符串可能会是一个很长的字符串)，使用Trie树的匹配方式，依然需要对d进行循环遍历，就像朴素模式匹配那样。Trie树减少的只是在Trie树中重合的部分，所以时间复杂会相当高。那么，KMP算法呢？对于KMP算法，我们要清楚一点。KMP算法是给模式串生成next函数，在多模式的情况下，我们需要生成很多的next函数，再对每个模式进行匹配。这显然也并不理想。

  基于以上这两点，我们的AC算法诞生了。

1.原理

  AC为了克服Trie树中无效匹配和KMP算法需要一个一个去匹配，设计了一种新的算法。算法中需要维护三个函数，分别是：

  success:从一个状态成功转移到另一个状态(有时也叫goto表或是success表)。

  failure:从一个状态按照普通流程会匹配失败，这时我们要通过failure函数来做状态跳转。

  emits:命中一个模式串(也称为output表)。

  从上面的状态转移图中就可以看出来，整个节点+实线就是success函数；而虚线就是failure函数；红色节点则是emits函数。

代码实现过程及说明

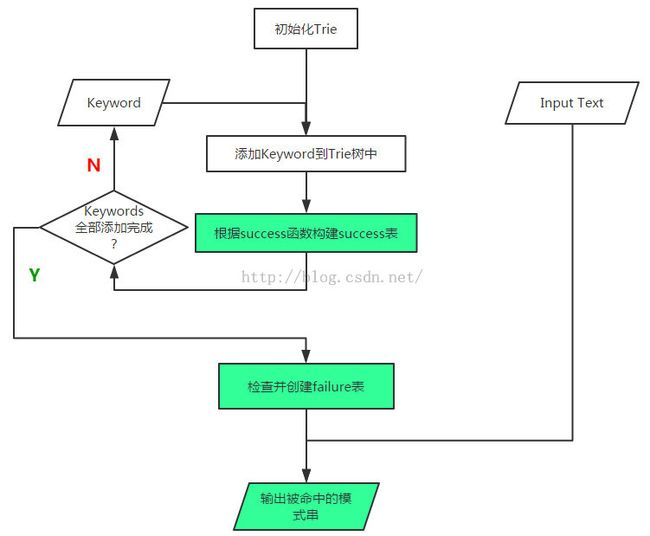
0.整体实现过程流程图

  

1.创建Trie树

  其实AC自动机是建立在Trie的基础之上的，从上面的状态转移图中就可以获得这一信息。而在AC算法的3个函数中的success函数就是一种Trie树。

/**
     * 构造一棵trie树
     * 
     * @param trieConfig
     */
    public Trie(TrieConfig trieConfig) {
        this(trieConfig, true);
    }

    public Trie(TrieConfig trieConfig, boolean ascii) {
        this.trieConfig = trieConfig;
        if (ascii) {
            this.rootState = new AsciiState();
        } else {
            this.rootState = new UnicodeState();
        }
    }

2.success表的创建

  从上面我们知道，success函数的功能就是构建一个棵Trie树。关键是如何构建，因为这个Trie树的构建和我们之前说的那并不完全相同。

  在AC算法中，我们把Trie树中的节点就直接称为状态(State).在创建状态转移表的过程中，则是利用了递推的思想。我们在添加字典的过程中，其实是去计算当前字符对应的下一下状态。详细过程，请参见如下代码：

/**
     * 转移到下一个状态
     *
     * @param character       希望按此字符转移
     * @param ignoreRootState 是否忽略根节点，如果是根节点自己调用则应该是true，否则为false
     * @return 转移结果
     */
    private State nextState(Character character, boolean ignoreRootState) {
        State nextState = this.success.get(character);
        if (!ignoreRootState && nextState == null && this.rootState != null) {
            nextState = this.rootState;
        }
        return nextState;
    }

    @Override
    public State nextStateIgnoreRootState(Character character) {
        return nextState(character, true);
    }

    @Override
    public State addState(Character character) {
        State nextState = nextStateIgnoreRootState(character);
        if (nextState == null) {
            nextState = new UnicodeState(this.depth + 1);
            this.success.put(character, nextState);
        }
        return nextState;
    }

3.failure表的创建

  failure表的创建是一个广度优先搜索的过程。在这个过程中，我们通过不断遍历状态Trie树。详细编码过程如下：

/**
     * 建立failure表
     */
    private void constructFailureStates() {
        Queue<State> queue = new LinkedBlockingDeque<State>();

        // 第一步，将深度为1的节点的failure设为根节点
        for (State depthOneState : this.rootState.getStates()) {
            depthOneState.setFailure(this.rootState);
            queue.add(depthOneState);
        }
        this.failureStatesConstructed = true;

        // 第二步，为深度 > 1 的节点建立failure表，这是一个bfs
        while (!queue.isEmpty()) {
            State currentState = queue.remove();

            for (Character transition : currentState.getTransitions()) {
                State targetState = currentState.nextState(transition);
                queue.add(targetState);

                State traceFailureState = currentState.failure();
                while (traceFailureState.nextState(transition) == null) {
                    traceFailureState = traceFailureState.failure();
                }
                State newFailureState = traceFailureState.nextState(transition);
                targetState.setFailure(newFailureState);
                targetState.addEmit(newFailureState.emit());
            }
        }
    }

4.emits命中(output表的创建)

  关于output表的创建，其实跟Trie树中的结束结点标志很类似。都是在模式串的末尾对状态进行修改的过程。而output表则是在状态节点对象中以组合的方式来体现。

/**
     * 添加一个模式串
     * 
     * @param keyword
     */
    public void addKeyword(String keyword) {
        ...
        currentState.addEmit(keyword);
    }
    
    /**
     * 添加一个匹配到的模式串（这个状态对应着这个模式串)
     *
     * @param keyword
     */
    public void addEmit(String keyword) {
        if (this.emits == null) {
            this.emits = new TreeSet<String>();
        }
        this.emits.add(keyword);
    }

代码下载：

http://download.csdn.net/detail/u013761665/9206401