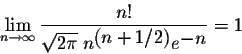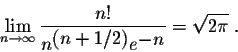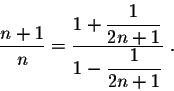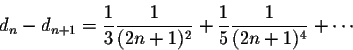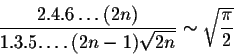poj1423

偏数学题：主要用到Stirling公式

1。用Stirling公式

公式和证明如下：

An important formula in applied mathematics as well as in probability is the Stirling's formula known as 

 

 

where  is used to indicate that the ratio of the two sides goes to 1 as n goes to . In other words, we have 

 

 

or 

 

 

 

Proof of the Stirling's Formula

First take the log of n! to get 

 

 

Since the log function is increasing on the interval , we get 

 

 

for . Add the above inequalities, with , we get 

 

 

Though the first integral is improper, it is easy to show that in fact it is convergent. Using the antiderivative of  (being ), we get 

 

 

Next, set 

 

 

We have 

 

 

Easy algebraic manipulation gives 

 

 

Using the Taylor expansion 

 

 

for -1 < t < 1, we get 

 

 

This implies 

 

 

We recognize a geometric series. Therefore we have 

 

 

From this we get

1.

the sequence   is decreasing;

2.

the sequence   is increasing.

This will imply that  converges to a number C with 

 

 

and that C > d₁ - 1/12 = 1 - 1/12 = 11/12. Taking the exponential of d_n, we get 

 

 

The final step in the proof if to show that . This will be done via Wallis formula (and Wallis integrals). Indeed, recall the limit 

 

 

Rewriting this formula, we get 

 

 

Playing with the numbers, we get 

 

 

Using the above formula 

 

 

we get 

 

 

Easy algebra gives 

 

 

since we are dealing with constants, we get in fact . This completes the proof of the Stirling's formula.

AC code：

# include <stdio.h> # include <math.h> int n; const   double  e  =   2.7182818284590452354 ,   pi   =   3.141592653589793239 ; double  f( int a ){     return   log10 (  sqrt (  2   *   pi   *  a ) )  +  a  *   log10 ( a  /  e );}int main(){    int cas ,  ans;     double  i ,  s;        scanf(  " %d " ,   & cas );         while ( cas --  )    {        scanf(  " %d " ,   & n );         if ( n  <   100000  )        {             for ( s = 0 ,  i = 1 ; i <= n; i ++  )                s  +=   log10 ( i );        }         else  s  =  f( n );        ans  =  (int)s;         if ( ans  <=  s )            ans ++ ;                 printf (  " %d/n " ,  ans );    }         return   0 ;}

 

2。用 位数=[ lg1+lg2+……lg(N-1)+lgN ] + 1。

数很大时，速度会慢，TLE。。

所以如上述AC代码，小于100000时，可以用这种方法，再大的话最好用Stiring公式。

运用Stirling公式写的AC了的C代码：

#include<stdio.h>
#include<math.h>

const double E = 2.7182818284590452354, PI = 3.141592653589793239;

int main()
{
	int n,i;
	int value;
	double stirlingValue;
	int result;
	scanf("%d",&n);
	for(i=0;i<n;i++){
		scanf("%d",&value);
		
		if(value==0||value==1){
			result=1;
		}else{
			stirlingValue=log10(value/E)*value+log10(sqrt(2*PI*value));
			
			result=(int)stirlingValue;
			result+=result<stirlingValue?1:0;
		}
		
		printf("%d\n",result);
	}
	return 0;
}