机器学习理论与实战（十二）神经网络

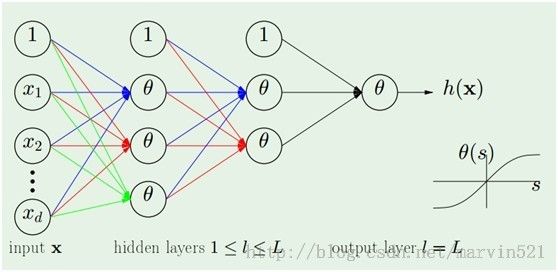
       神经网络又火了，因为深度学习火了，所以必须增加个传统神经网络的介绍,尤其是back propagation算法。很简单，俺也就不舞文弄墨的说复杂咯，神经网络模型如（图一）所示：

（图一）

         （图一）中的神经网络模型是由多个感知器（perceptron）分几层组合而成，所谓感知器就是单层的神经网络（准确的说应该不叫神经网络咯），它只有一个输出节点，如（图二）所示：

(图二)  感知器

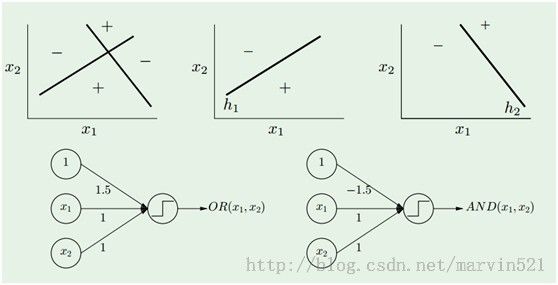
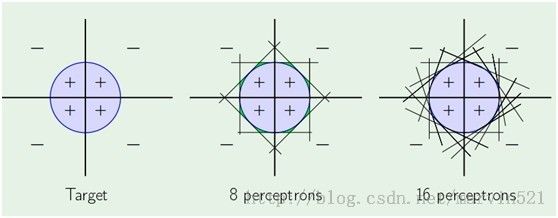
         一个感知器就相当于一个线性分类器，而一层神经网络有多个隐藏节点的，就是多个感知器的组合，那么它其实就是多个线性分类器组合形成非线性分类器咯，如（图三）所示：

（图三）

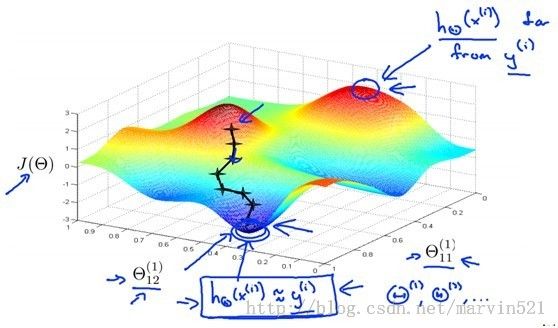
        一层感知器拟合能力就颇为强大，而多层的感知器组合起来，那拟合能力更没得说，可惜的是拟合能力虽然强大，但是求出准确拟合参数的算法不是太好，容易陷入局部最小，而且BP算法很“擅长”陷入局部最小，所谓局部最小，如（图四）所示，网络的权重被随机初始化后，然后求得梯度，然后用梯度更新参数，如果初始化的参数的点选择的不恰当，当梯度为0的点可能是一个使得代价J局部最小的点，而不是全局最小的，自然得到的网络权重也不是最好的。BP算法一直都有这样的问题，而且也容易因为网络规模大导致过拟合，好在最近深度学习提了一系列的trick改善了这些问题。比如用贪心预训练来改进初始化参数，相当于找到了一个好的初始点，严格的说是在正负阶段里主动修改了J的“地形”，这是个人的一些理解，最后再结合标签用传统的BP算法继续进行寻找全局最小，这个BP算法的作用在深度学习里也叫权重微调，当然BP不是唯一的权重微调算法，各种微调的宗旨只有一个：求取目标函数的梯度，更新参数。另外深度学习里利用稀疏和dropout来阻止过拟合。

（图四）

       介绍了BP算法的作用，那么就来看下BP算法的原理，也很简单，就是把目标函数各层的权重进行求导，因为我们要更新权重就是要求出梯度，然后利用梯度更新权重。网络从输入到最终的输出经过了多层的函数处理，求导的时候就是对这个复合函数的链式求导。为了不把BP算法说复杂，我找了一个最简单的网络，如（图五）所示：

（图五）

       （图五）中的网络只有三层：输入层X，隐藏层h和输出层y。中间有两个权重W1和W2，刚开始都是随机初始化的。神经网络的训练分为两个过程，第一过程就是从输入训练样本，层层计算到最终输出y,这个过程前向传播（forward propagation）。接着计算输出y和真实标签的差，这个可以作为简单的目标函数，我们的目标就是使得这个目标函数在所有的训练集上最小，说白了就是找个目标函数的最小值，找它就要求梯度，然后更新参数。接着就是求梯度咯，把目标函数对W2和W1求导咯，这个过程叫反向传播(back propagation)。下面（图六）简单的演示下这个两个过程：

（图六）前向传播和反向传播

       注意下前向传播得到保留中间变量，比如a1,a2, 这些在反向传播中都要是用到的，整个原理也很简单，就是目标函数对各层的权重的求导，因为是复合函数，所以要链式求导。有了梯度，用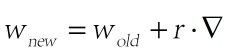 这个经典更新方式来跟新权重就行咯,其中r 是个自己设置的学习率，不要过大，大了会产生学习晃动的情况，倒三角就是梯度咯。另外输出层不一定要用（图六）中的目标函数，自己可以根据情况来指定不同的目标函数，哪怕你最后输出再加个支持向量机都行，只要你可以求导，得到梯度就行，事实上hinton的一个弟子最近就在做这个事情。个人发挥自己的智慧来改进模型吧^.^，另外，卷积神经网络的参数更新过程也是类似，都免不了用BP算法来求导。

下面是模仿这两个过程的代码：

import math
import random
import string

random.seed(0)

# calculate a random number where:  a <= rand < b
def rand(a, b):
    return (b-a)*random.random() + a

# Make a matrix (we could use NumPy to speed this up)
def makeMatrix(I, J, fill=0.0):
    m = []
    for i in range(I):
        m.append([fill]*J)
    return m

# our sigmoid function, tanh is a little nicer than the standard 1/(1+e^-x)
def sigmoid(x):
    return math.tanh(x)

# derivative of our sigmoid function, in terms of the output (i.e. y)
def dsigmoid(y):
    return 1.0 - y**2

class NN:
    def __init__(self, ni, nh, no):
        # number of input, hidden, and output nodes
        self.ni = ni + 1 # +1 for bias node
        self.nh = nh
        self.no = no

        # activations for nodes
        self.ai = [1.0]*self.ni
        self.ah = [1.0]*self.nh
        self.ao = [1.0]*self.no
        
        # create weights
        self.wi = makeMatrix(self.ni, self.nh)
        self.wo = makeMatrix(self.nh, self.no)
        # set them to random vaules
        for i in range(self.ni):
            for j in range(self.nh):
                self.wi[i][j] = rand(-0.2, 0.2)
        for j in range(self.nh):
            for k in range(self.no):
                self.wo[j][k] = rand(-2.0, 2.0)

        # last change in weights for momentum   
        self.ci = makeMatrix(self.ni, self.nh)
        self.co = makeMatrix(self.nh, self.no)

    def update(self, inputs):
        if len(inputs) != self.ni-1:
            raise ValueError('wrong number of inputs')

        # input activations
        for i in range(self.ni-1):
            #self.ai[i] = sigmoid(inputs[i])
            self.ai[i] = inputs[i]

        # hidden activations
        for j in range(self.nh):
            sum = 0.0
            for i in range(self.ni):
                sum = sum + self.ai[i] * self.wi[i][j]
            self.ah[j] = sigmoid(sum)

        # output activations
        for k in range(self.no):
            sum = 0.0
            for j in range(self.nh):
                sum = sum + self.ah[j] * self.wo[j][k]
            self.ao[k] = sigmoid(sum)

        return self.ao[:]


    def backPropagate(self, targets, N, M):
        if len(targets) != self.no:
            raise ValueError('wrong number of target values')

        # calculate error terms for output
        output_deltas = [0.0] * self.no
        for k in range(self.no):
            error = targets[k]-self.ao[k]
            output_deltas[k] = dsigmoid(self.ao[k]) * error

        # calculate error terms for hidden
        hidden_deltas = [0.0] * self.nh
        for j in range(self.nh):
            error = 0.0
            for k in range(self.no):
                error = error + output_deltas[k]*self.wo[j][k]
            hidden_deltas[j] = dsigmoid(self.ah[j]) * error

        # update output weights
        for j in range(self.nh):
            for k in range(self.no):
                change = output_deltas[k]*self.ah[j]
                self.wo[j][k] = self.wo[j][k] + N*change + M*self.co[j][k]
                self.co[j][k] = change
                #print N*change, M*self.co[j][k]

        # update input weights
        for i in range(self.ni):
            for j in range(self.nh):
                change = hidden_deltas[j]*self.ai[i]
                self.wi[i][j] = self.wi[i][j] + N*change + M*self.ci[i][j]
                self.ci[i][j] = change

        # calculate error
        error = 0.0
        for k in range(len(targets)):
            error = error + 0.5*(targets[k]-self.ao[k])**2
        return error


    def test(self, patterns):
        for p in patterns:
            print(p[0], '->', self.update(p[0]))

    def weights(self):
        print('Input weights:')
        for i in range(self.ni):
            print(self.wi[i])
        print()
        print('Output weights:')
        for j in range(self.nh):
            print(self.wo[j])

    def train(self, patterns, iterations=1000, N=0.5, M=0.1):
        # N: learning rate
        # M: momentum factor
        for i in range(iterations):
            error = 0.0
            for p in patterns:
                inputs = p[0]
                targets = p[1]
                self.update(inputs)
                error = error + self.backPropagate(targets, N, M)
            if i % 100 == 0:
                print('error %-.5f' % error)


def demo():
    # Teach network XOR function
    pat = [
        [[0,0], [0]],
        [[0,1], [1]],
        [[1,0], [1]],
        [[1,1], [0]]
    ]

    # create a network with two input, two hidden, and one output nodes
    n = NN(2, 2, 1)
    # train it with some patterns
    n.train(pat)
    # test it
    n.test(pat)



if __name__ == '__main__':
    demo()

转载请注明来源： http://blog.csdn.net/marvin521/article/details/9886643

参考文献：

      [1] Learning From Data. Yaser S.Abu-Mostafa

    [2] machine learning.Andrew Ng